[学习笔记]舞蹈链(DLX)(C++指针版)

概述

舞蹈链(Dancing Links X)是一种能较高效地解决精确覆盖问题的暴力算法

模板题：洛谷P4929

精确覆盖问题

精确覆盖问题是这样一类问题：

给定一个01矩阵，要求选出其中一些行，使得这些行组成的新矩阵每一列恰好有一个1

例如

对于矩阵

\[\left( \begin{matrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{matrix} \right) \]

一组解为1,4,5行

层层深入

基本暴力

枚举所有行组合，然后检验

显然会T到飞起

稍作思考的暴力(X算法)

假设我们选了一行，那么与这行有重叠部分的行就不能选了，我们将其删除

同时，我们把已经被覆盖的列也删除

原问题就变成了规模更小的精确覆盖问题

如果最后没有办法覆盖某一列，就更改之前的操作，继续暴力

直到最后所有列被覆盖(找到一组解)或是始终有某些列不能被覆盖(无解)

以上面的矩阵为例，我们先选择第1行，删去这一行和与它有重合部分的行，把已经覆盖的列也删去，得到

\[\left( \begin{matrix} 1&0&1&1 \\ 1&0&1&0 \\ 0&1&0&1 \end{matrix} \right) \]

接下来问题变成了一个规模更小的精确覆盖问题

假设我们再选择第1行，得到

\[\left( \begin{matrix} 1&1 \end{matrix} \right ) \]

再选第1行，得到空矩阵

说明找到一组解

回顾过程，我们依次删掉了原矩阵的1,4,5行

Donald E. Knuth大师的暴力

下面的图片均来自: https://www.cnblogs.com/grenet/p/3145800.html

上面的稍作思考的暴力复杂度依然很高

为什么复杂度会很高呢？

我们发现有大量时间花费在对矩阵的修改上

那么有没有办法降低修改矩阵的时间开销呢？

当然是有的，Donald E. Knuth大师给出了解决方案——交叉十字循环双向链

首先由于我们只关心覆盖，所以只考虑1的位置，0就可以丢掉啦

把1的位置像下面这张图一样存起来：

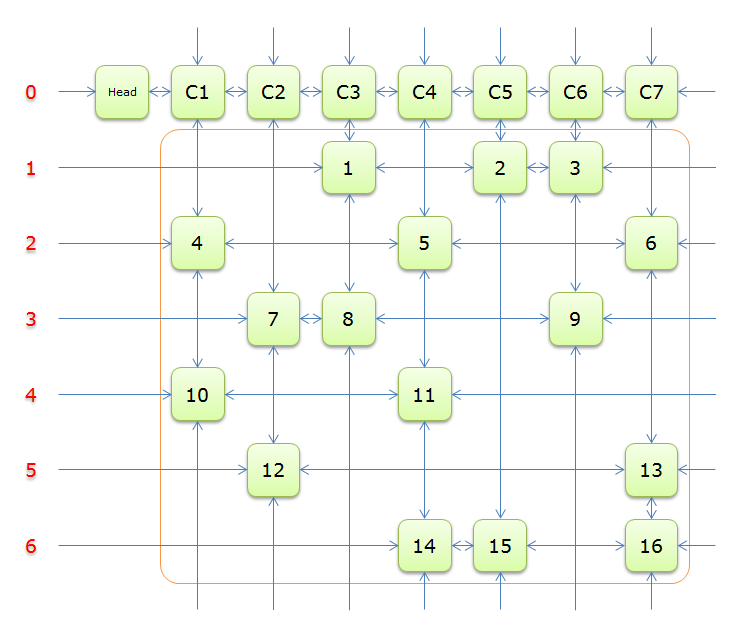
对应矩阵

\[\left( \begin{matrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{matrix} \right) \]

其中第一行的head是整个链表的入口，C1,C2,...是各列的入口

接下来我们来看看具体操作

链表构建

首先是链表元素的结构体

struct Node {
	Node *left, *right, *up, *down, *head; //指向四个方向和列的表头
	int row, cnt; //记录行号(用于记录答案)及列元素个数
} *head, *cols[MAXN];

其中cnt只有C1,C2,...的有用，和一个优化有关 ，不加也慢不了多少（少过两个点而已）

构建链表的过程

head = new Node;
for (int i = 0; i < m; ++i) {
	cols[i] = new Node;
	cols[i]->row = -1;
	cols[i]->head = cols[i];
}
for (int i = 1; i < m; ++i) cols[i]->left = cols[i - 1];
for (int i = m - 2; i >= 0; --i) cols[i]->right = cols[i + 1];
cols[0]->left = head, head->right = cols[0];
cols[m - 1]->right = head, head->left = cols[m - 1];

Node *p[MAXN]; //记录列尾
for (int i = 0; i < m; ++i) p[i] = cols[i];
for (int i = 0; i < n; ++i) {
	Node *nplast = NULL;
	for (int j = 0; j < m; ++j)
		if (mtx[i][j]) {
			Node *np = new Node;
			np->row = i;
			//插入列中
			np->up = p[j], p[j]->down = np;
			np->down = p[j]->head, p[j]->head->up = np;
			np->head = p[j]->head;
			
			//插入行中
			if (nplast) {
				np->right = nplast->right;
				nplast->right->left = np;
				np->left = nplast, nplast->right = np;
			} else {
				np->left = np->right = np;
				nplast = np;
			}
			p[j] = np;
			++np->head->cnt;
		}

}

选定行

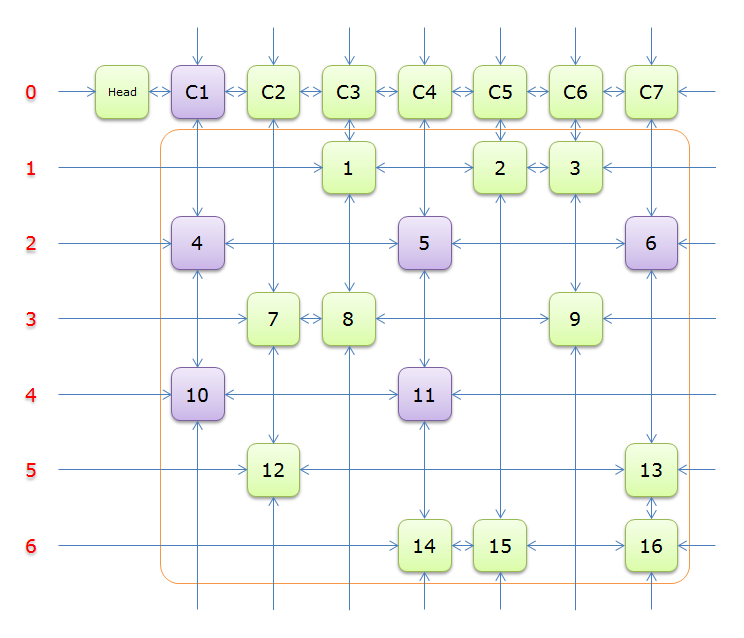
选定某一行时，对照第二种暴力，我们要删去的有：这一行、这一行能覆盖的列、与这一行有重叠部分的其它行

比如选定第二行来覆盖第一列，那么我们要删掉下图中的紫色节点

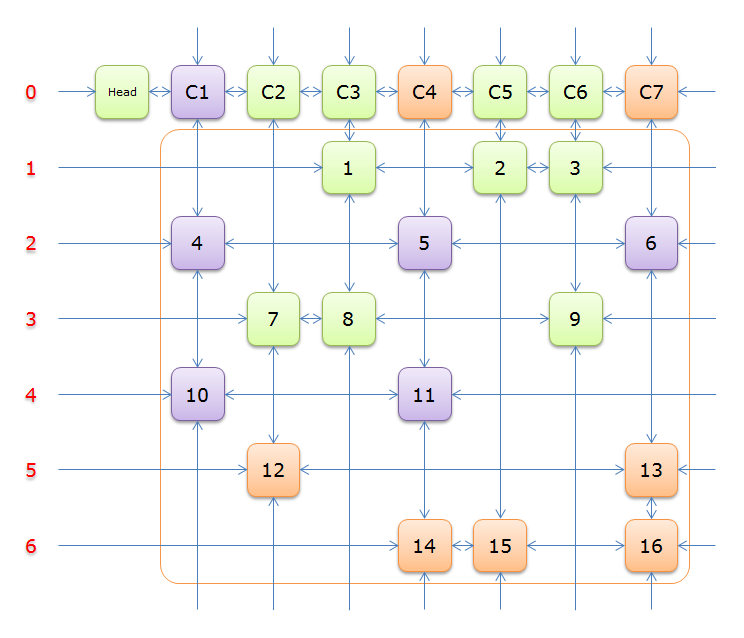
然后删除已经覆盖的列和能覆盖它们的其它行，即下图中的橙色节点

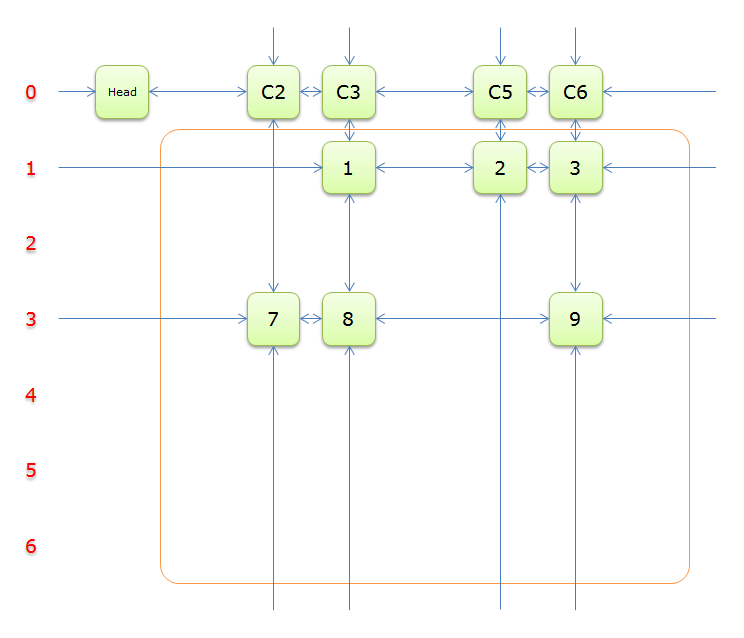
最后得到

代码如下

// p为要选择的行的某个元素
for (Node *pp = p->right; pp != p; pp = pp->right) { //找到相关的列
	for (Node *ppc = pp->down; ppc != pp; ppc = ppc->down) { // 能覆盖相关列的行
		if (ppc != pp->head)
			for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
				ppr->up->down = ppr->down, ppr->down->up = ppr->up;
				--ppr->head->cnt;
			}
	}
	pp->head->left->right = pp->head->right;
	pp->head->right->left = pp->head->left;
}
for (Node *ppc = p->down; ppc != p; ppc = ppc->down) {
	if (ppc != p->head)
		for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
			ppr->up->down = ppr->down, ppr->down->up = ppr->up;
			--ppr->head->cnt;
		}
}
p->head->left->right = p->head->right;
p->head->right->left = p->head->left;

撤销

就是上面的选行的逆操作

for (Node *pp = p->right; pp != p; pp = pp->right) { //相关的列
	for (Node *ppc = pp->down; ppc != pp; ppc = ppc->down) { //包含相关列的行
		if (ppc != pp->head)
			for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
				ppr->up->down = ppr->down->up = ppr;
				++ppr->head->cnt;
			}
	}
	pp->head->left->right = pp->head->right->left = pp->head;
}
for (Node *ppc = p->down; ppc != p; ppc = ppc->down) {
	if (ppc != p->head)
		for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
			ppr->up->down = ppr->down->up = ppr;
			++ppr->head->cnt;
		}
}
p->head->left->right = p->head->right->left = p->head;

关于前面提到的优化

每次尝试覆盖某一列的时候，我们找剩余元素最少的那列覆盖

这样可以优化一下时间

完整的代码：

// luogu P4929
#include <cstdio>
#include <cstring>
#include <iostream>

const int MAXN = 1010;

struct Node {
	Node *left, *right, *up, *down, *head; //指向四个方向和列的表头
	int row, cnt; //记录列表及列元素个数
} *head, *cols[MAXN];

int mtx[MAXN][MAXN], n, m;
int ans[MAXN], top;

void init();
bool solve();

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 0; i < n; ++i)
		for (int j = 0; j < m; ++j)
			scanf("%d", &mtx[i][j]);
	init();
	if (solve()) {
		//puts("One solution found:");
		for (int i = 0; i < top; ++i) printf("%d ", ans[i] + 1);
		puts("");
	} else puts("No Solution!");


	return 0;
}
void init() {
	top = 0;
	head = new Node;
	for (int i = 0; i < m; ++i) {
		cols[i] = new Node;
		cols[i]->row = -1;
		cols[i]->head = cols[i];
	}
	for (int i = 1; i < m; ++i) cols[i]->left = cols[i - 1];
	for (int i = m - 2; i >= 0; --i) cols[i]->right = cols[i + 1];
	cols[0]->left = head, head->right = cols[0];
	cols[m - 1]->right = head, head->left = cols[m - 1];
	
	Node *p[MAXN]; //记录列尾
	for (int i = 0; i < m; ++i) p[i] = cols[i];
	for (int i = 0; i < n; ++i) {
		Node *nplast = NULL;
		for (int j = 0; j < m; ++j)
			if (mtx[i][j]) {
				Node *np = new Node;
				np->row = i;
				//插入列中
				np->up = p[j], p[j]->down = np;
				np->down = p[j]->head, p[j]->head->up = np;
				np->head = p[j]->head;
				
				//插入行中
				if (nplast) {
					np->right = nplast->right;
					nplast->right->left = np;
					np->left = nplast, nplast->right = np;
				} else {
					np->left = np->right = np;
					nplast = np;
				}
				p[j] = np;
				++np->head->cnt;
			}

	}
}
bool solve() {
	if (head->right == head) return 1; //还有列未被覆盖

	// 找到元素个数最少的列，能有效降低复杂度
	Node *c = head->right;
	for (Node *p = c->right; p != head; p = p->right)
		if (p->cnt < c->cnt) c = p;
	
	for (Node *p = c->down; p != c; p = p->down) {//枚举选择的行
		for (Node *pp = p->right; pp != p; pp = pp->right) { //相关的列
			for (Node *ppc = pp->down; ppc != pp; ppc = ppc->down) { //包含相关列的行
				if (ppc != pp->head)
					for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
						ppr->up->down = ppr->down, ppr->down->up = ppr->up;
						--ppr->head->cnt;
					}
			}
			pp->head->left->right = pp->head->right;
			pp->head->right->left = pp->head->left;
		}
		for (Node *ppc = p->down; ppc != p; ppc = ppc->down) {
			if (ppc != p->head)
				for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
					ppr->up->down = ppr->down, ppr->down->up = ppr->up;
					--ppr->head->cnt;
				}
		}
		p->head->left->right = p->head->right;
		p->head->right->left = p->head->left;

		// 记录答案，继续搜索
		ans[top++] = p->row;
		if (solve()) return 1;
		--top;

		// 撤销选择行的操作
		for (Node *pp = p->right; pp != p; pp = pp->right) { //相关的列
			for (Node *ppc = pp->down; ppc != pp; ppc = ppc->down) { //包含相关列的行
				if (ppc != pp->head)
					for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
						ppr->up->down = ppr->down->up = ppr;
						++ppr->head->cnt;
					}
			}
			pp->head->left->right = pp->head->right->left = pp->head;
		}
		for (Node *ppc = p->down; ppc != p; ppc = ppc->down) {
			if (ppc != p->head)
				for (Node *ppr = ppc->right; ppr != ppc; ppr = ppr->right) {
					ppr->up->down = ppr->down->up = ppr;
					++ppr->head->cnt;
				}
		}
		p->head->left->right = p->head->right->left = p->head;
	}
	return 0;
}
//Rhein_E