[学习笔记]圆方树&广义圆方树
引入
偶尔,我们会遇到一些要在无向图/仙人掌上做的问题,这些问题如果在树上就会比较方便,那么我们就开始考虑能不能把原图等效成一棵树,然后就可以方便地乱搞了?
圆方树就是一种将无向图/仙人掌变成树的数据结构
一般无向图的圆方树
构建
对于一般的无向图,不满足树形结构的部分无非是边双联通分量、点双联通分量
构建圆方树时我们处理点双联通分量(一般无向图中两个点、一条边的也算一个点双)
具体做法是原图中每个点是圆点
对于每个点双,我们新建一个方点
点双中原有的边全部拆掉,而里面的圆点(原图上的点)都向这个方点连边
当然原图中的点可能属于多个点双
举个例子就是:
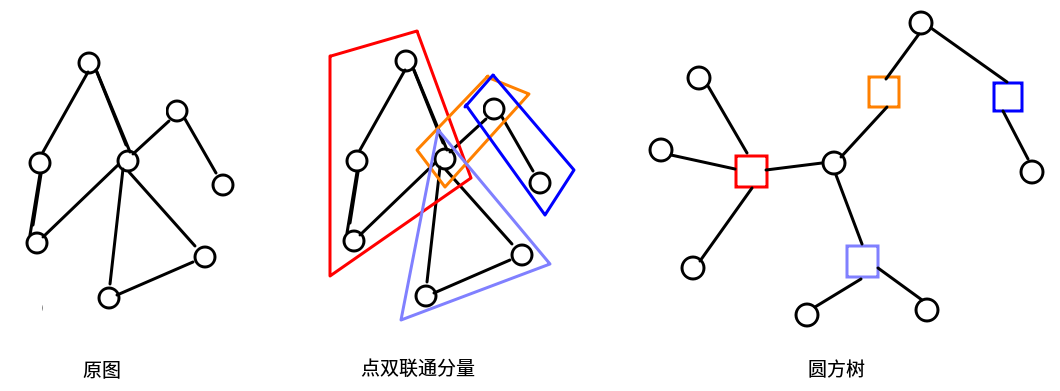
然后它就变成了一棵树,然后什么树链剖分、点分治、虚树、树形dp甚至LCT等各种(duliu)算法就可以在上面搞啦!唯一需要注意的是方点和圆点的维护方式可能不同
具体的构建过程写法不唯一,可以一边\(Tarjan\)一边建树,也可以存下属于哪些点双然后推倒重建
推倒重建版:
void Tarjan(int u, int fa) {
dfn[u] = low[u] = ++idx;
for (int i = G.head[u]; ~i; i = G.edge[i].next) {
int v = G.edge[i].v;
if (v == fa) continue;
if (!dfn[v]) {
stk[stop++] = v;
Tarjan(v, u);
low[u] = std::min(low[u], low[v]);
if (low[v] >= dfn[u]) {
int p; ++tot;
do {
p = stk[--stop];
bel[p].push_back(tot);
} while (p ^ v);
bel[u].push_back(tot);
}
} else low[u] = std::min(low[u], dfn[v]);
}
}
void rebuild() {
G.init();
for (int i = 1; i <= N; ++i) for (int j = 0; j < bel[i].size(); ++j)
G.insert(i, bel[i][j]);
}
性质
这样建出的圆方树具有以下性质:
- 显然建出的是一堆无根树构成的森林,原图上联通的点圆方树(森林)上也联通
- 相邻的点形状必定不同
- 所有度数\(\ge 1\)的圆点在原图中都是割点
例题
还是要从例题入手,才能发现圆方树性质的妙用,所以:
仙人掌的圆方树
upd 2019.4.9 咕了好久,我终于来填坑了!!
好像上面那个叫广义圆方树,这个才是正统圆方树来着,我又学错顺序了??
仙人掌
无向仙人掌是指一条边至多在一个简单环中的无向图
构建
大体上类似于广义圆方树,但这里我们对一个环建方点,而不在同一个环上的两个圆点直接连边
就比如:
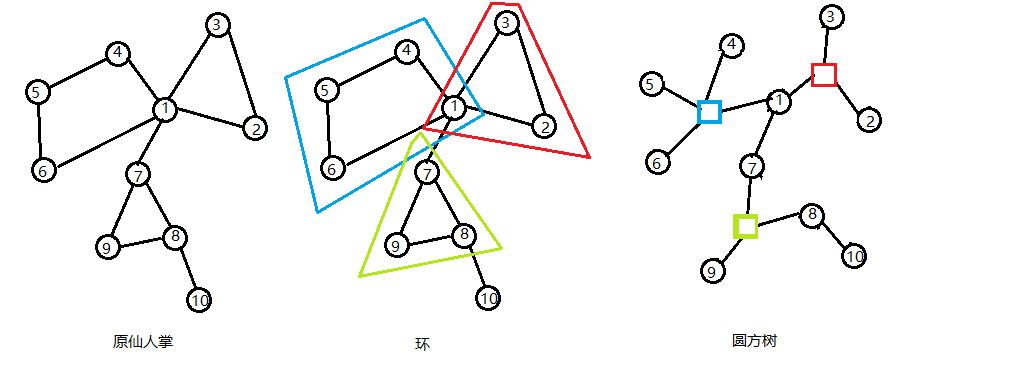
性质
可能存在圆方边和圆圆边,但没有方方边
然后容易发现原仙人掌的子仙人掌对应的圆方树是整个圆方树上的一个联通块
例题
首先建出圆方树,然后考虑赋边权
为了是原仙人掌上的最短路对应圆方树上两点间的路径,我们按如下方式赋边权:
- 指定一个圆点为圆方树的根,然后我们把一个方点的父亲叫做这个方点对应的环的根
- 若一个在环上的圆点不是环的根,它到对应方点的边权为到环的根的最短距离
- 环的根到环所对应的方点的边权为0
然后仿照在树上查询两点路径一样
但是这里需要分类讨论:
- 若\(lca\)是圆点,那么答案就是路径长度
- 若\(lca\)是方点,则找到进入这个环的两个点,这两个点之间的有两条路径,比较一下选较短的
如何找到2中的两个点呢?
如果写的是倍增,可以方便求出
如果写的是树链剖分,这两个点有两种情况:1.一个是dfs序比\(lca\)大1的点,一个是最后经过的\(top\);2.最后经过的两个\(top\)
环上路径可以用距离前缀和,再记录一下每个环的边权和求出
代码(倍增)
#include <cstdio>
#include <cstring>
#include <iostream>
#define MAXN 10005
#define MAXM 20005
typedef long long LL;
struct Graph {
struct Edge {
int v, next; LL w;
Edge(int _v = 0, int _n = 0, LL _w = 0):v(_v), next(_n), w(_w) {}
} edge[MAXM << 2];
int head[MAXN << 1], cnt;
void init() { memset(head, -1, sizeof head); cnt = 0; }
void add_edge(int u, int v, int w) { edge[cnt] = Edge(v, head[u], w); head[u] = cnt++; }
void insert(int u, int v, int w) { add_edge(u, v, w); add_edge(v, u, w); }
};
char gc();
LL read();
void Tarjan(int, int);
LL query(int, int);
void dfs(int);
int N, M, Q;
int dep[MAXN << 1], dist[MAXN << 1], anc[MAXN << 1][17];//圆方树上的深度、到根的距离、祖先
LL sum[MAXN], sumd[MAXN];//sum:距离前缀和,也就是搜索树上到根的距离。sumd:每个环的边权和
int dfn[MAXN], low[MAXN], bcc_cnt, idx, stk[MAXN], top;;//Tarjan用到的
Graph G, T;//G:原图。T:圆方树
int main() {
G.init(), T.init();
N = read(), M = read(), Q = read();
for (int i = 1; i <= M; ++i) {
int u = read(), v = read(); LL w = read();
G.insert(u, v, w);
}
Tarjan(1, 0);
dfs(1);
while (Q--) {
int u = read(), v = read();
printf("%lld\n", query(u, v));
}
return 0;
}
inline char gc() {
static char buf[1000000], *p1, *p2;
if (p1 == p2) p1 = (p2 = buf) + fread(buf, 1, 1000000, stdin);
return p1 == p2 ? EOF : *p2++;
}
inline LL read() {
LL res = 0, op; char ch = gc();
while (ch != '-' && (ch < '0' || ch > '9')) ch = gc();
op = (ch == '-' ? ch = gc(), -1 : 1);
while (ch >= '0' && ch <= '9') res = (res << 1) + (res << 3) + ch - '0', ch = gc();
return res * op;
}
void Tarjan(int u, int fa) {
dfn[u] = low[u] = ++idx;
stk[top++] = u;
for (int i = G.head[u]; ~i; i = G.edge[i].next) {
int v = G.edge[i].v; LL w = G.edge[i].w;
if (v == fa) continue;
if (!dfn[v]) {
sum[v] = sum[u] + w;
Tarjan(v, u);
low[u] = std::min(low[u], low[v]);
if (low[v] > dfn[u]) T.insert(u, v, w);//非树边只可能是返祖边,可以这样判
} else if (dfn[v] < low[u]) {//这里这样判也是一样的原因
low[u] = dfn[v];
++bcc_cnt;
sumd[bcc_cnt] = sum[u] + w - sum[v];
for(int j = top - 1; stk[j] ^ v; --j) {
int p = stk[j];
T.insert(N + bcc_cnt, p, std::min(sum[p] - sum[v], sumd[bcc_cnt] - sum[p] + sum[v]));
}
T.insert(N + bcc_cnt, v, 0);
}
}
--top;
}
void dfs(int u) {
dep[u] = dep[anc[u][0]] + 1;
for (int i = 1; i < 17 && anc[u][i - 1]; ++i) anc[u][i] = anc[anc[u][i - 1]][i - 1];
for (int i = T.head[u]; ~i; i = T.edge[i].next) {
int v = T.edge[i].v; LL w = T.edge[i].w;
if (v == anc[u][0]) continue;
dist[v] = dist[u] + w;
anc[v][0] = u, dfs(v);
}
}
LL query(int x, int y) {
int lca; LL res = dist[x] + dist[y];
if (dep[x] < dep[y]) std::swap(x, y);
for (int i = 16; i >= 0; --i) if (dep[anc[x][i]] >= dep[y]) x = anc[x][i];
if (x == y) lca = x;
else {
for (int i = 16; i >= 0; --i) if (anc[x][i] ^ anc[y][i]) x = anc[x][i], y = anc[y][i];
lca = anc[x][0];
}
if (lca <= N) return res - (dist[lca] << 1);//lca是圆点
else {//lca是方点
if (dfn[x] > dfn[y]) std::swap(x, y);
return res - dist[x] - dist[y] + std::min(sum[y] - sum[x], sumd[lca - N] - sum[y] + sum[x]);
}
}
//Rhein_E


