day10T3改错记

题面

有\(n + m\)个判断题，事先知道有\(n\)道答案为\(true\)，\(m\)道答案为\(false\)。每答一道题，你将知道是否答对。问用最优策略，期望最少答错多少道题？

题外话

题解并没有写出重点，导致我们一排六个人推了一下午式子没推出来，结果正确思路是看图得结论……

解析

显然最优策略是选多的那个答案，一样就随机选一个

这个问题就可以转化为在下面的图中从\((n, m)\)走到\((0, 0)\)（假设\(n \ge m\)，另外的情况\(swap\)一下效果一样的）

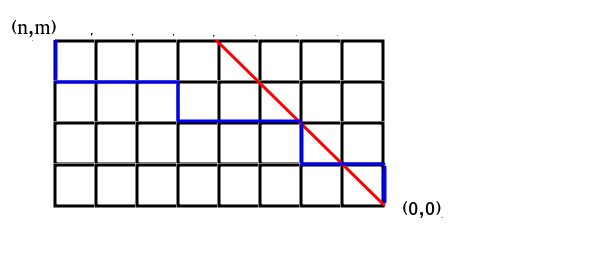
答案是任意一条从\((n, m)\)到\((0, 0)\)的路径（比如蓝线）

根据最优策略，一定是在红线左下的时候答\(true\)，在右上的时候答\(false\)，在红线上就随机走

首先你一定至少答对\(n\)道题，因为左下部分的横线你一定能答对，右上部分的竖线你也一定能答对

加起来恰好是\(n\)

那么剩下的就是在红线上的点有\(\frac{1}{2}\)的贡献

枚举每个红点\((i, i)\)，那么有所有经过这个点的路径总共有这个点之前的\({{n + m - 2 \cdot i} \choose {n - i}}\)乘上这个点之后的\({{2 \cdot i} \choose {i}}\)条，题目求期望，再除以总方案数\({n + m} \choose {n}\)

也就得到期望答对多少道题：

\[n + \frac{\sum_{i = 1}^{\min(n, m)} {n + m - 2 \cdot i \choose n - i} \cdot {2 \cdot i \choose i}}{2 \cdot {n + m \choose n}} \]

拿\(n + m\)减这个就是答案了

代码

又是自带大常数的丑陋代码……

#include <cstdio>
#include <cstring>
#include <iostream>
#define MAXN 500005

typedef long long LL;
const int mod = 998244353;

int qpower(int, int, int);
void pre_work();
int comb(int, int);

int N, M, ans, fact[MAXN << 1], ifact[MAXN << 1], inv[MAXN << 1];

inline void inc(int &x, int y) { x += y; if (x >= mod) x -= mod; }
inline void dec(int &x, int y) { x -= y; if (x < 0) x += mod; }
inline int add(int x, int y) { x += y; return x >= mod ? x - mod : x; }
inline int sub(int x, int y) { x -= y; return x < 0 ? x + mod : x; }

int main() {
	freopen("fft.in", "r", stdin);
	freopen("fft.out", "w", stdout);

	scanf("%d%d", &N, &M);
	if (N < M) std::swap(N, M);
	pre_work();
	for (int i = 1; i <= M; ++i)
		inc(ans, (LL)comb(N + M - (i << 1), N - i) * comb(i << 1, i) % mod);
	ans = (LL)ans * qpower(comb(N + M, N) * 2ll % mod, mod - 2, mod) % mod;
	printf("%d\n", sub(M, ans));

	return 0;
}
int qpower(int x, int y, int p) {
	int res = 1;
	while (y) {
		if (y & 1) res = (LL)res * x % p;
		x = (LL)x * x % p; y >>= 1;
	}
	return res;
}
void pre_work() {
	fact[0] = fact[1] = ifact[0] = ifact[1] = inv[1] = 1;
	for (int i = 2; i <= (N + M); ++i) {
		fact[i] = (LL)fact[i - 1] * i % mod;
		inv[i] = (LL)(mod - mod / i) * inv[mod % i] % mod;
		ifact[i] = (LL)ifact[i - 1] * inv[i] % mod;
	}
}
int comb(int n, int m) {
	return (LL)fact[n] * ifact[m] % mod * ifact[n - m] % mod;
}
//Rhein_E