BZOJ4003[JLOI2015]城池攻占(可并堆+懒惰标记)
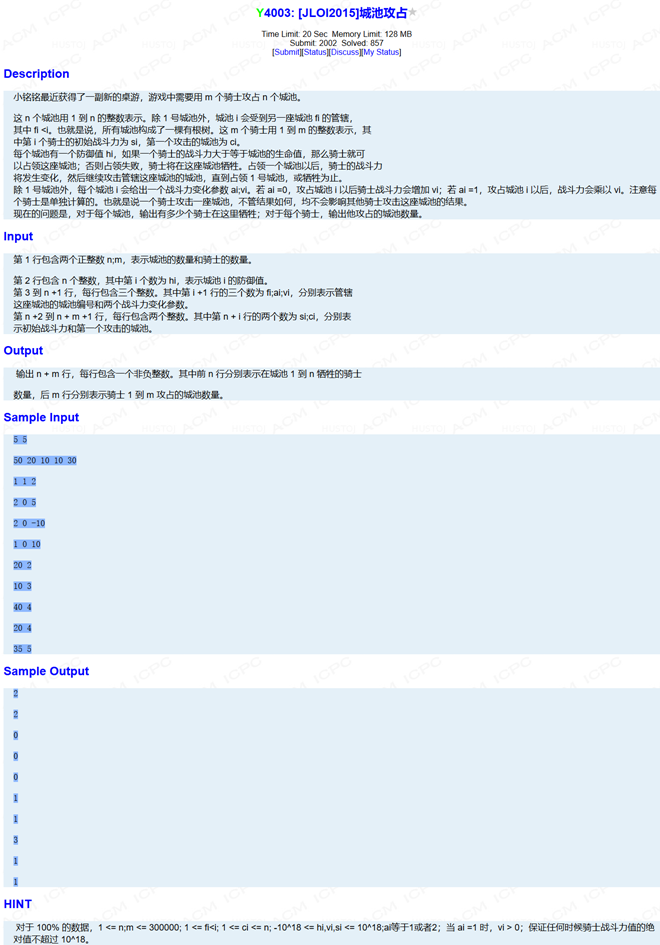
题面:
思路:直接考虑每个骑士不方便,就考虑每座城池会被哪些骑士攻占。如果一个骑士到不了儿子节点,那他肯定到不了父亲节点,所以可以对每座城池建一个小根堆,维护能攻占这座城池的骑士,递归处理子树,然后把子树的堆合并进来,当堆顶骑士攻击力小于城池生命值时弹出,同时该城池的答案++。对每个骑士,可以在上述过程中记录他弹出的位置,攻占的城池数就是dep[st]-dep[ed],为方便统计,根节点深度记为1。
注意下放标记。。。。然后先乘后加。。。。
P.S.刚开始果断倍增,然后光荣地MLE了,不过据说3倍3倍地倍增可以减小一半内存然后AC。。。。
代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <vector> 5 #define MAXN 300000 6 #define MAXM 300000 7 8 typedef long long LL; 9 struct LeftistTree { 10 LeftistTree *son[2]; 11 LL mul, add; 12 int id, d; 13 LeftistTree(int _id = 0) { id = _id; son[0] = son[1] = NULL; mul = 1; add = d = 0; } 14 } * root[MAXN + 5]; 15 int a[MAXN + 5], st[MAXM + 5], end[MAXM + 5], ans[MAXN + 5], dep[MAXN + 5], N, M; 16 LL h[MAXN + 5], v[MAXN + 5], s[MAXM + 5]; 17 std::vector<int> son[MAXN + 5]; 18 19 char gc(); 20 LL read(); 21 void print(LL); 22 void dfs(int); 23 LeftistTree *merge(LeftistTree *, LeftistTree *); 24 LeftistTree *push(LeftistTree *, int); 25 LeftistTree *pop(LeftistTree *); 26 void pushDown(LeftistTree *); 27 int top(LeftistTree *); 28 29 int main() { 30 memset(root, 0, sizeof root); 31 N = read(), M = read(); 32 for (int i = 1; i <= N; ++i) 33 h[i] = read(); 34 for (int i = 2; i <= N; ++i) { 35 son[read()].push_back(i); 36 a[i] = read(); 37 v[i] = read(); 38 } 39 for (int i = 1; i <= M; ++i) { 40 s[i] = read(), st[i] = read(); 41 root[st[i]] = push(root[st[i]], i); 42 } 43 dep[1] = 1; 44 dfs(1); 45 for (int i = 1; i <= N; ++i) 46 print(ans[i]), putchar('\n'); 47 for (int i = 1; i <= M; ++i) 48 print(dep[st[i]] - dep[end[i]]), putchar('\n'); 49 50 return 0; 51 } 52 inline char gc() { 53 static char buf[1000000], *p1, *p2; 54 if (p1 == p2) p1 = (p2 = buf) + fread(buf, 1, 1000000, stdin); 55 return p1 == p2 ? EOF : *p2++; 56 } 57 inline LL read() { 58 LL res = 0, op; 59 char ch = gc(); 60 while (ch != '-' && (ch < '0' || ch > '9')) ch = gc(); 61 op = (ch == '-' ? ch = gc(), -1 : 1); 62 while (ch >= '0' && ch <= '9') 63 res = (res << 1) + (res << 3) + ch - '0', ch = gc(); 64 return res * op; 65 } 66 inline void print(LL x) { 67 static int buf[30]; 68 if (!x) putchar('0'); 69 else { 70 if (x < 0) x = -x, putchar('-'); 71 while (x) buf[++buf[0]] = x % 10, x /= 10; 72 while (buf[0]) putchar('0' + buf[buf[0]--]); 73 } 74 } 75 void pushDown(LeftistTree *rt) { 76 if (rt->mul > 1) { 77 for (int i = 0; i < 2; ++i) 78 if (rt->son[i]) { 79 rt->son[i]->mul *= rt->mul; 80 rt->son[i]->add *= rt->mul; 81 s[rt->son[i]->id] *= rt->mul; 82 } 83 rt->mul = 1; 84 } 85 if (rt->add) { 86 for (int i = 0; i < 2; ++i) 87 if (rt->son[i]) { 88 rt->son[i]->add += rt->add; 89 s[rt->son[i]->id] += rt->add; 90 } 91 rt->add = 0; 92 } 93 } 94 void dfs(int u) { 95 for (int i = 0; i < son[u].size(); ++i) { 96 dep[son[u][i]] = dep[u] + 1; 97 dfs(son[u][i]); 98 root[u] = merge(root[u], root[son[u][i]]); 99 } 100 while (1) { 101 if (!root[u]) break; 102 int p = top(root[u]); 103 if (s[p] >= h[u]) break; 104 root[u] = pop(root[u]); 105 ans[u]++; 106 end[p] = u; 107 } 108 if (root[u]) { 109 if (a[u]) root[u]->mul *= v[u], root[u]->add *= v[u], s[root[u]->id] *= v[u]; 110 else root[u]->add += v[u], s[root[u]->id] += v[u]; 111 } 112 } 113 LeftistTree *merge(LeftistTree *x, LeftistTree *y) { 114 if (!x) return y; 115 if (!y) return x; 116 if (s[x->id] > s[y->id]) std::swap(x, y); 117 pushDown(x); 118 x->son[1] = merge(x->son[1], y); 119 if (!x->son[0] || (x->son[1] && x->son[1]->d > x->son[0]->d)) 120 std::swap(x->son[1], x->son[0]); 121 if (x->son[1]) x->d = x->son[1]->d + 1; 122 else x->d = 0; 123 return x; 124 } 125 LeftistTree *push(LeftistTree *rt, int v) { 126 LeftistTree *tmp = new LeftistTree(v); 127 return merge(rt, tmp); 128 } 129 LeftistTree *pop(LeftistTree *rt) { 130 pushDown(rt); 131 LeftistTree *res = merge(rt->son[0], rt->son[1]); 132 delete rt; 133 return res; 134 } 135 int top(LeftistTree *rt) { 136 return rt->id; 137 }