可持久化线段树
可持久化线段树
可持久化
可持久化数据结构总是可以保留每一个历史版本,并且支持操作的不可变特性。
对于这个说法,我表示非常赞同,因为可持久化的标志就是在修改的过程中仍然可以保持原子树的性质,对于直接全局更改,倒不如把原来的一部分留下,用新的空间来记录当前更改后的值,只改我们需要得到那一部分,因此我们开始研究可持久化的数据结构,帮助我们解决涉及可持久化的一类题目。
在本篇中我们着重讲可持久化线段树这一知识点
可持久化数组
题目描述:如题,你需要维护这样的一个长度为 \(N\) 的数组,支持如下几种操作
- 在某个历史版本上修改某一个位置上的值
- 访问某个历史版本上的某一位置的值
此外,每进行一次操作(对于操作2,即为生成一个与查询版本完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从1开始编号,版本0表示初始状态数组)
题目几乎已经把可持久化拍到了脸上,我们考虑对于这一道题来说,第一次见到数组的可持久化,肯定是不好维护的
我们考虑线段树,先把这个数组按照线段树的方式建出来,但是这个题不要求我们区间求和,所以我们不需要\(\mathrm{pushup}\) 操作,先在叶子节点建出树来即可
对于样例的话 \(59~46~14~87~41\)

大概就是长成这样
这时候我们开始有了单点修改的操作
0 1 1 14
即把初始状态的数组进行更改,把 \(a_1\) 改成 \(14\)
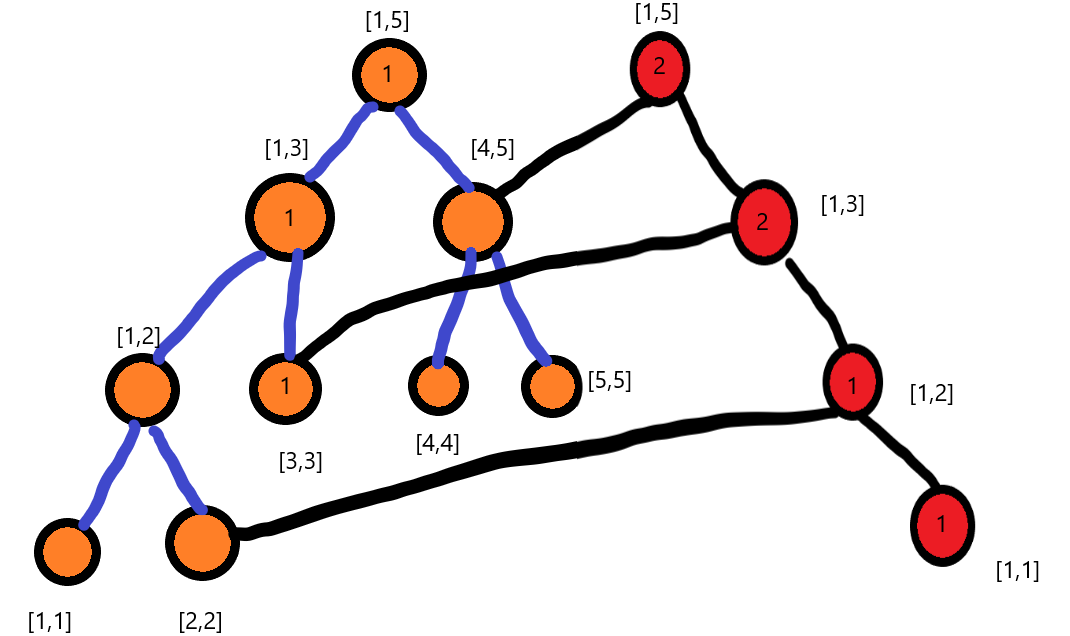
这时候我们就要想,现在我们要保持原数组不变,那我们不妨再开一个节点,然后让这个新的子树的 [1,2]区间的左儿子连向这个节点,这样的话这个图长成这样,这个属实是难画啊,我们就简洁画一下了

红色的节点是我们的新建节点,橙色的节点是之前的节点,我们发现,此时我们如果需要重新建一棵树的话太浪费了,有很多树的节点都没有被修改却白白浪费掉,但是我们发现每改一个点,只需要改从根节点到它的每个祖先节点,这些边组成了一条链,因此每次我们只需要新建 \(\log n\) 条边,我们的空间范围可能就会因此大一些,因为我们每次都存下了每一条边。
而且还有一个关键的信息,我们每次都会是要建新的根节点的,我们可以根据根节点来确定是第几次修改的
这道题的完整代码如下:
首先这里是要支持修改的,所以我们要写动态开点线段树,对于每个点,我们肯定是有一侧要建新点的,直接在从根节点往下传递时处理即可
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
int n, m, T, ans, cnt, opt, x, k, pre;
int a[N], rt[N];
struct tree {
int val, ls, rs;
}tr[N << 5];
inline void build(int &p, int l, int r) {
p = ++cnt;
if (l == r) return tr[p].val = a[l], void(); //建立新节点,出现新的返回值
int mid = (l + r) >> 1; //build一棵新的子树,一定要记得动态开点
build(tr[p].ls, l, mid); //前面写的是取址,后面会给这个ls赋值的,所以要这么写
build(tr[p].rs, mid + 1, r);
}
inline void update(int &p, int pre, int l, int r, int x, int k) {//取址后方便新建节点
p = ++cnt; // p就是我们需要新建的节点的编号
tr[p] = tr[pre]; //当前点继承树pre的信息
if (l == r) return tr[p].val = k, void();
int mid = (l + r) >> 1;
if (x <= mid) update(tr[p].ls, tr[pre].ls, l, mid ,x, k); //这里处理的时候一定是要继承同侧的
else update(tr[p].rs, tr[pre].rs, mid + 1, r, x, k);
}
inline int query(int p, int l, int r, int x) { //同上
if (l == r) return tr[p].val;
int mid = (l + r) >> 1;
if (x <= mid) return query(tr[p].ls, l, mid, x);
else return query(tr[p].rs, mid + 1, r, x);
}
int main(){
#ifndef ONLINE_JUDGE
freopen("1.in", "r", stdin);
freopen("1.out", "w", stdout);
#endif
read(n, m);
rep(i, 1, n) read(a[i]);
build(rt[0], 1, n);
rep (i, 1, m) {
read(pre), read(opt);
if (opt == 1) {
read(x, k);
update(rt[i], rt[pre], 1, n, x, k);
}
else {
read(x);
write(query(rt[pre], 1, n, x), '\n');
rt[i] = rt[pre];
}
}
return 0;
}
//write:RevolutionBP
可持久化线段树(主席树)
题目要求:给定一个数组 \(a\),m次操作查询区间第 \(k\) 小值
\(1\le n,m\le 2\times 10^5\) \(1\le a_i \le 10^9\)
我们考虑这个题的本质就是要求每次查询在 \(\log n\) 复杂度内找到静态区间的第 \(k\) 小值
那么就是我们要用 \(n\log n\) 复杂度预处理这个数组,那么这题就明显多了,线段树一定是必要的
但是这时候我们还要去想,我们用什么方式来处理这个数组
我们不妨用值域线段树来维护
首先我们要对这个序列进行一下离散化
对于 \(\forall i\in [1,n]\) 前 \(i\) 个点建一棵树,树上的每个节点 \([l,r]\) 就是存离散化以后值在 \([l,r]\) 之间的有多少个。那么这题就很好做了。我们对于区间 \(a_l\) 到 \(a_r\) 的查询时,分别取出 \(tree_{l-1}\) 和 \(tree_r\) 然后让两者的对应节点相减,每个点就代表了在这一段中每一个点在各个树上区间的出现次数,我们要查询第 \(k\) 小,如果对于当前节点的左儿子值为 \(a(a < k)\),那么很显然,我们就要在右儿子中找,此时我找的就不是第 \(k\) 小了,因为在右子树这棵子树中,应该是第 \(k - a\) 小
那么我们很好奇,这个算法和可持久化有什么关系呢?我们想,如果我们直接这么建树的空间复杂度是多少?
答案:\(2*n^2\)
这肯定是吃不消的,所以我们考虑能不能优化空间,答案是可以的,因为我们要是想要记录前 \(i\) 棵子树的值的话,第 \(i-1\) 棵子树必然也是能用上的,我们不妨就让我们当前节点继承上第 \(i-1\) 棵子树的值,然后再加上 \(a_i\) 这个点的贡献,对于样例,我们把树建出来,是不是就长成下面这样(空节点为 \(0\)),这样的话,我们建树的复杂度就只有 \(n \log n\)。
我们下面放出代码:
首先是离散化,离散化的话看起来很麻烦,其实我们可以理解成一个映射(如果你觉得很简单,说明你比我强太多了o(╥﹏╥)o)
对于每个点,我们找一下它的值的排名,所以cpy出来一个新数组 \(b\),然后让 \(b\) 进行排序并去重
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
int n, m, T, ans, l, r, k, cnt;
int a[N], b[N], rt[N];
struct tree{
int sum, lc, rc;
}tr[N << 5];
inline void update(int &p, int pre, int l, int r, int k) {
p = ++cnt;
tr[p] = tr[pre];
tr[p].sum ++;
if (l == r) return ;
int mid = (l + r) >> 1;
if (k <= mid) update(tr[p].lc, tr[pre].lc, l, mid, k);
else update(tr[p].rc, tr[pre].rc, mid + 1, r, k);
}
inline int query(int L, int R, int l, int r, int k) {
if (l == r) return l;
int x = tr[tr[R].lc].sum - tr[tr[L].lc].sum;//找一下左子树的sum
int mid = (l + r) >> 1;
if (x >= k) return query(tr[L].lc, tr[R].lc, l, mid, k);//递归左子树,不需要改变k
else return query(tr[L].rc, tr[R].rc, mid + 1, r, k - x);//递归右子树,需要改变k
}
int main(){
#ifndef ONLINE_JUDGE
freopen("1.in", "r", stdin);
freopen("1.out", "w", stdout);
#endif
read(n, T);
rep(i, 1, n) read(a[i]), b[i] = a[i];
sort (b + 1, b + 1 + n);
int len = unique(b + 1, b + 1 + n) - b - 1;
rep (i, 1, n) {
int p = lower_bound(b + 1, b + len + 1, a[i]) - b;
update(rt[i], rt[i - 1], 1, len, p);
}
while (T--) {
read(l, r, k);
ans = query(rt[l - 1], rt[r], 1, len, k);
write(b[ans], '\n');
}
return 0;
}
//write:RevolutionBP


 浙公网安备 33010602011771号
浙公网安备 33010602011771号