简单数学(只有知识点,持续更新)
简单数学
常见概念和符号
数论常见符号
-
整除符号 \(x\mid y\),表示 \(x\) 整除 \(y\) ,即 \(x\) 是 \(y\) 的因数
-
取模符号 \(x \bmod y\) ,表示 \(x\) 除以 \(y\) 以后的余数
-
互质符号 \(x~\bot~y\) ,表示 \(x\) ,\(y\) 互质
-
最大公约数 \(\gcd(x,y)\)
-
最小公倍数 \(\text{lcm} (x,y)\)
-
求和符号:\(\sum\) 符号,表示满足特定条件的数的和
\(\sum _{i=1} ^{n} ai\) 表示 \(a_1\sim a_n\) 的和
\(\sum_{S\subseteq T} |S|\)
-
求积符号:\(\Pi\) 符号,表示满足特定条件的数的积
\(\Pi_{i=1}^n\) 表示 \(n!\)
\(\Pi _{i=1}^{n} a_i\) 表示从 \(a_1\sim a_n\) 的积
\(\Pi _{x\mid d} x\) 表示 \(d\) 的所有因数的乘积 -
整除符号:\(\mid\) ,\(a \mid b\) 表示 \(a\) 是 \(b\) 的约数 \(b\) 不被 \(a\) 整除记作 \(a \nmid b\) 。
-
同余符号:\(\equiv\) ,\(a\equiv b \pmod c\) 表示 \(\dfrac a c -\lfloor \dfrac a c \rfloor=\dfrac b c-\lfloor \dfrac b c \rfloor\) 或者说 \(a/c\) 和 \(b/c\) 的余数相同
-
卷积符号:
*卷积分很多种,常见的有
加法卷积:\[ h=f*g=\sum_{i+j==n} f(i)g(j) \]乘法卷积(狄利克雷卷积)(满足交换律和结合律):
\[ h=f*g=\sum_{d\mid n}f(d)g(\dfrac n d) \]位运算卷积:
\[ h=f*g=\sum_{i\oplus j==n} f(i)g(j) \]
数论函数
数论函数指定义域为正整数的函数。数论函数也可以视作一个数列。
恒等函数
\(I(x)=1(x)= 1\)
元函数
又称单位元
\(\varepsilon(n)=[n==1]\)
markdown格式为$\varepsilon$
单位函数
\(id_k(n)=n^k\),\(id_1(n)\) 通常简记为 \(id(n)=n\)
积性函数
若 \(f(n)\) 表示 \(f(1)=1\) 且 \(\forall x,y \in N_+\) \(\gcd(x,y)=1\) 都有 \(f(xy)=f(x)f(y)\),则 \(f(n)\) 为积性函数
若 \(f(n)\) 表示 \(f(1)=1\) 且 \(\forall x,y \in N_+\) 都有 \(f(xy)=f(x)f(y)\),则 \(f(n)\) 为完全积性函数
欧拉函数
\(φ(n)\) :定义:1~n中与n互质的数的个数
公式:
莫比乌斯函数
\(k_i\) 表示质因数分解后每一个质因子的指数
我们一般表示为 \(\mu(x)\)
- \(\exists k_i\ge 2\),\(\mu(x)=0\)
- \(\forall k_i=1\),\(\mu(x)=(-1)^y\) (\(y\) 是质因数分解后有几项)
- \(x=1\) ,\(\mu(x)=1\)
如:
\(\mu(6)=1\) \(\mu(7)=-1\) \(\mu(8)=0\)
设 \(s(n)=\sum_{i=d\mid n}^{n} \mu (i)\)
如 \(s(6) = \mu(1) +\mu(2) +\mu(3) +\mu(6)\)
那么:
- 当 \(n=1\),\(s(n)=1\)
- 当 \(n>1\),\(s(n)=0\)
对于2的证明:
首先我们对于 \(n\) 因式分解:\(n=p_1^{\alpha_1}\times p_2^{\alpha_2}\times\dots\times p_k^{\alpha_k}\) (\(k\ge 1\))
那么我们的每一个 \(d\) 都有:\(d=p_1^{\beta_1}\times p_2^{\beta_2}\times\dots\times p_k^{\beta_k}\) (\(\forall i \in [1,k]\) \(0\le\beta_i\le \alpha_i\))
那么我们算一下 \(\mu(d)\) 可知,我们只需要考虑,如果\(\exists i \in [1,k]\),\(\beta_i\ge 2\) 则原式为 \(0\)
所以我们只需要看里面有多少个1即可
所以我们用组合数算一下:
我们这时候看一下二项式定理:
钦定 \(a=1\) \(b=-1\)
所以 \(s(x)\) 必然等于 \(=0\),得证
约数个数函数
\(d(x)=\sum_{d\mid n}1\),不用多说了,就是约数个数
卷积公式
\(\varepsilon*F=F\),\(F\) 是任意数论函数
证明:\(\varepsilon*F=\sum_{d\mid n}\varepsilon(\dfrac n d)F(d)\)
只有当 \(n = d\) 时,\(\dfrac n d\) 为1,此时的值就是 \(F(n)\),所以得证
\(\varepsilon=\mu * 1\),即 \([n=1]=\sum_{d\mid n}\mu(d)\),使得所有 \(1\) 的限制都变成了可以被预处理的 \(\mu(d)\)
证明:由于 \(\mu * 1=\sum_{d\mid n}\mu(d)\),前面我们已经证明了当 \(n\not =1\) 的时候原式值为 \(0\),当 \(n=1\) 时值为 \(1\),所以得证
\(id=\varphi*1\),即 \(n=\sum_{d\mid n}\varphi(d)\)
\(\mu * id=\varphi\),由前面几个合起来就有了
\(\mu * d=1\),可以据此进行反演
导数公式
\((C)^{'}=0\) \((x^\mu)'=\mu x^{\mu-1}\)
\((a^x)'=a^x\ln x\) ( \(a\) 为常数) \((\sin x)'=\cos x\)
\((\cos x)'=-\sin x\) \((\tan x)'=\sec^2x\)
\((\cot x)'=-\csc^2x\) \((\sec x)'=\sec x \cot x\)
\((\csc x)'=-\csc x\cot x\) \((\ln x)'=\dfrac{1}{x}\)
\(({\log_a}^x)'=\dfrac{1}{x\ln a}\) \((e^x)'=e^x\)
加减公式:
\((u\pm v)'=u'\pm v'\) \((Cu)'=Cu'\) (C是常数)
\((uv)'=u'v+uv'\) \((\dfrac{u}{v})'=(\dfrac{u'v-uv'}{v^2})\)
复数
设\(a,b\)为实数,\(i^2=-1\),形如\(a+bi\)的数叫复数,其中\(i\)被称为虚数单位,复数域是目前已知最大的域
在复平面中,\(x\) 代表实数,\(y\) 轴(除原点外的点)代表虚数,从原点\((0,0)\)到\((a,b)\)的向量表示复数\(a+bi\)
模长:从原点\((0,0)\)到点\((a,b)\)的距离,即\(\sqrt{a^2+b^2}\)
幅角:假设以逆时针为正方向,从xx轴正半轴到已知向量的转角的有向角叫做幅角
计算:平行四边形法则(其实就是分配律),注意这里的\(i^2\)为-1:
几何定义:复数相乘,模长相乘,幅角相加(至今我也没看懂)
\((a+bi)\times (c+di)=ac+bdi^2+bci+adi=ac-bd+(bc+ad)i\)
同时,我们由向量的知识迁移到复数上来,定义 复数的模 就是复数所对应的向量的模。
复数 \(z=a+bi\) 的模 \(|z|=\sqrt{a^2+b^2}\)
于是为了方便,我们常把复数 \(z=a+bi\) 称为点 \(Z\)
由向量的知识我们发现,虚数不可以比较大小
复数满足交换律,结合律,对加法的分配律
当两个虚数实部相等,虚部互为相反数时,这两个复数互为 共轭复数。
即 \(z=a+bi\) 的共轭复数为 \(z=a-bi\)
CZY数学三大定理
CZY数学三大公理指的是以下三大公理:二是质数定理、大于二质数构造公理、质数自反性公理。
三大定理介绍
「二是质数定理」
内容:定义 \(2\) 是质数
证明:反证法:由于 \(2\) 不是合数,所以 \(2\) 是质数
如此厉害的结论竟然是 \(nekko\) 在赖床的时候发现的,当时的 \(nekko\) 躺在床上玩双人成行,在玩的过程中就发现了这一伟大的定理,从此,数学界的一个新世界,由 \(czy\) 构建的一个崭新的数学世界诞生了
「大于二质数构造公理」
内容:如果一个整数大于 \(2\),并且不能被任何一个小于这个数的质数整除,那么这个数是质数。
证明:太高深了,不太会证,希望有神犇来帮忙证明一下
「质数自反性公理」
如果一个整数是质数,那么它是质数。
证明:需要用到逻辑学中的大量文献,这里暂时略过了
挫折与发展
在CZY提出「三大公理」后,有人提出「非陈数学」,即否定了公理一而保留公理二三。令人遗憾的是,此人在研究了一段时间后,发现「非陈数学」中并不存在任何质数。但是,此人却在「非陈数学」中证明了「黎曼猜想」不成立。所以说,"祸兮福所倚,福兮祸所伏"。
他人的评价
"数学的基石,文化的先行,宇宙的奠定"——ZTB瞻望「三大公理」
最新的进展
CZY指出,由绝对值的知识,有 \(|-1| = 1\);由行列式的知识,有 \(|-1| = -1\)。因此得出结论 \(2=0\).
位运算
一般均是在二进制下来说
基本运算
1.与 (&) 两个对应位都为 \(1\) 时才为 \(1\)
2.或 (|) 只要两个对应位中有一个 \(1\) 时就为 \(1\)
3.异或(^) 只有两个对应位不同时才为 \(1\)
取反(~)
把0变成1,把1变成0
补码:在二进制表示下,正数和 的补码为其本身,负数的补码是将其对应正数按位取反后加一。
应用:\(\text{lowbit}(x)=(x)\&(-x)\) 取出最后一个等于1的位数,具体原因想一想
左移和右移
num<<i 表示将 \(num\) 的二进制表示向左移动1位所得的值。
num>>i 表示将 \(num\) 的二进制表示向右移动1位所得的值。
注意:+ 和-的优先级高于左移右移
高精度
#include<iostream>
#include<string.h>
#include<stdio.h>
#include<cstdlib>
#include<algorithm>
#define base 100000
#define cut 5
#define L 10000
using namespace std;
struct Big{
int len;
long long num[L];
Big(){
len=1;
memset(num,0,sizeof(num));
}
Big operator=(const Big &a){
len=a.len;
for(int i=0;i<len;i++) num[i]=a.num[i];
return *this;
}
long long &operator[](int a){
return num[a];
}
long long operator[](int a)const{
return num[a];
}
friend istream&operator>>(istream&,Big&);
friend ostream&operator<<(ostream&,Big&);
};
int operator>(const Big a,const Big b){
if(a.len!=b.len){
if(a.len>b.len) return 1;
return 0;
}
for(int i=a.len-1;i>=0;i--)
if(a[i]>b[i]) return 1;
return 0;
}
int operator==(const Big a,const Big b){
if(a.len!=b.len) return 0;
for(int i=0;i<a.len;i++)
if(a[i]!=b[i])
return 0;
return 1;
}
int operator<(const Big a,const Big b){
if(a>b || a==b)return 0;
return 1;
}
Big operator+(Big a,Big b){
Big ret;
long long carry=0;
for(int i=0;;i++){
ret[i]=a[i]+b[i]+carry;
carry=ret[i]/base;
ret[i]%=base;
if(i>=a.len&&i>=b.len&&carry==0)
break;
}
ret.len=min(L,max(a.len,b.len)+10);
while(ret.len>0&&ret[ret.len-1]==0)
ret.len--;
if(ret.len==0)
ret.len=1;
return ret;
}
Big operator+(Big a,int b){
long long carry=b;
for(int i=0;;i++){
a[i]+=carry;
carry=a[i]/base;
a[i]%=base;
if(a[i]==0 && carry==0 && i>=a.len)
break;
}
a.len=min(L,a.len+10);
while(a.len>0 && a[a.len-1]==0) a.len--;
return a;
}
Big operator*(Big a,Big b){
Big ret;
for(int i=0;i<a.len;i++)
for(int j=0;j<b.len;j++) ret[i+j]+=a[i]*b[j];
long long carry=0;
for(int i=0;;i++){
ret[i]+=carry;
carry=ret[i]/base;
ret[i]%=base;
if(ret[i]==0 && carry==0 && i>=a.len+b.len-1) break;
}
a.len=min(L,a.len+b.len+10);
while(a.len>0 && a[a.len-1]==0) a.len--;
return a;
}
Big operator*(Big a,int b){
long long carry=0;
for(int i=0;;i++){
carry+=a[i]*b;
a[i]=carry%base;
carry/=base;
if(carry==0&&a[i]==0&&i>=a.len) break;
}
a.len=min(L,a.len+10);
while(a.len>0&&a[a.len-1]==0) a.len--;
return a;
}
Big operator-(Big a,Big b){
long long carry=0;
for(int i=0;;i++){
a[i]-=b[i]+carry;
if(a[i]<0) carry=(-a[i]/base+1);
else carry=0;
a[i]+=carry*base;
if(carry==0&&i>=b.len) break;
}
while(a.len>0&&a[a.len-1]==0) a.len--;
return a;
}
Big operator-(Big a,int b){
long long carry=b;
for(int i=0;;i++){
a[i]-=carry;
if(a[i]<0) carry=(-a[i]/base+1);
else carry=0;
a[i]+=carry*base;
if(carry==0) break;
}
while(a.len>0 && a[a.len-1]==0) a.len--;
return a;
}
Big operator/(Big a,int b){
long long carry=0;
for(int i=a.len-1;i>=0;i--){
a[i]+=carry*base;
carry=a[i]%b;
a[i]/=b;
}
while(a.len>0&&a[a.len-1]==0) a.len--;
return a;
}
Big operator%(const Big a,int b){
return a-(a/b)*b;
}
int main(){
return 0;
}
数论
整除性质
同余性质
最大公约数与最小公倍数
若干个数所有约数中的共同的最大数是最大公约数,倍数中共同的最小数是最小公倍数
一般两个数的最大公约数是 \(\gcd\) 最小公倍数是 \(\mathrm{lcm}\)
\(\gcd(a,b)*\mathrm{lcm}(a,b)=a*b\)
求法:辗转相除
int gcd(int a,int b){return a%b==0?a:gcd(b,a%b);}
整除分块
整除分块是用于快速处理形似
的式子的办法
引理1
证明略
引理2
对于一个较大的 \(n\) 我们显然会发现,我们后面的这个下取整取值并不是每一次都随着 \(i\) 而变化的,它是呈块状分布的,同时这个下取整的值我们也能得到,应该是共有 \(2\sqrt n\) 个值
结论:
通过严谨的数学推理(打表) 我们发现实际上这些取值是有规律的,即
如果一个块的开始位置时 \(l\) 那么它的结束位置 \(r\) 就是 \(\lfloor \dfrac n {\lfloor \frac n l \rfloor} \rfloor\)
那么我们写程序的基本结构就很显然了
for(int l=1,r;l<=n;l=r+1) r=n/(n/l);
所以我们对于形如:
可以对 \(f(i)\) 可以直接前缀和预处理,就可以解决这道问题了
各种筛法
埃氏筛
用于统计从1-n中的质数
原理:从前往后筛,如果筛到一个数\(i\),然后把\(i\)的倍数都删了
时间复杂度:\(O(n\log n \log n)\) 基本可以跑到2e7
void statistics(int n){
for(int i=2;i<=n;i++){
if(!st[i]) prime[++k]=i;
for(int j=1;prime[j]*i<=n;j++){
st[prime[j]*i]=true;
}
}
}
线性筛
这个东西很重要,关系到后面的积性函数求解
先放一个代码:
void primes(int n){
for(int i=2;i<=n;i++){
if(!st[i]) prime[++k]=i;
for(int j=1;prime[j]*i<=n;j++){
st[i*prime[j]]=true;
if(!(i%prime[j])) break;
}
}
}
我们观察和上面那个的区别
发现无非就是多了一行if(i%prime[j]==0) break;
我们考虑对于这一行来说,它的意义本质上是筛到 \(i\) 的最小质因子时停止
我们给个证明:
首先我们假设我们的 \(i\) 筛到 \(prime_j\) 的时候结束
1. 对于 \(prime_j\) 我们有 \(prime_j\) 是 \(i\) 的最小质因子,原因是若不是的话,这个循环会提前的break掉,不会让我们跑到 \(j\) 这个位置
2. 对于 \(i\times prime_k(1\le k < j)\) 的最小质因子恒为 \(prime_k\),原因是 \(i\) 的最小质因子是 \(prime_j\) 对于 \(prime_k\) 恒小于 \(prime_j\)
3. 对于 \(i\times prime_k(k > j)\) 的最小质因子应该是 \(prime_j\),理由同上,这句话说明了,对于 \(i\times prime_k\) 来说,它在这个 \(prime_j\) 时已经被筛过一次了,所以不必要继续往后筛
由于每个点只会被最小质因子筛一次,这样线性筛的复杂度就可以被优化到 \(O(n)\) 了
欧拉筛
我们可以把这件求phi分成两步
k是质数
首先我们容易发现一个问题:如果\(k\)是质数,那么\(\varphi (k)\)显然等于\(k-1\),因为小于\(k\)的数都与\(k\)互质
所以我们可以把这一句:if(!vis[i]) p[++num]=i;再加上一句phi[i]=i-1;
-
\(i\bmod p=0\) 时
若 \(p\mid i\) 且 \(p\) 为质数 则 \(\varphi(i*p)\)=\(p*\varphi(i)\)
证明:
若 \(p \mid i\) 则可以推出 \(p\) 是 \(i\) 的一个质因子
我们发现:一个数的欧拉函数与每一项的次数无关
所以说
同时
发现两个式子除了 \(i*p\) 全部相同
所以我们可以推出 \(\varphi(i*p)\)=\(p*\varphi(i)\)
证毕
那么很显然在这一句中if(i%prime[j]==0) break;我们可以加上phi[prime[j]*i]=prime[j]*phi[i]
-
\(i\%p\not =0\) 时
\(p\) 一定是 \(i*p_j\) 的最小质因子
先把 \(\varphi(i)\) 的式子摆在这
\[\varphi(i)=i*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})...*(1-\frac{1}{p_k}) \]然后
\[\varphi(p*i)=p*i*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})...*(1-\frac{1}{p_k}*(1-\frac{1}{p})) \]我们把下面的式子除以上面的式子发现:
\[\varphi(p*i)/\varphi(i)=p*(1-\frac{1}{p})=p-1 \]把 \(\varphi(i)\) 挪到右边最后可以得到
\[\varphi(p*i)=\varphi(i)*(p-1) \]所以我们讨论完了所有的情况,可以得到最终式子:
inline void get_euler(int n) {
phi[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++cnt] = i, phi[i] = i - 1;
for (int j = 1; j <= cnt && prime[i] * j <= n; ++j) {
st[prime[j] * i] = true;
if (i % prime[j] == 0) {
phi[i * prime[j]] = phi[i] * (prime[j] -1);
break;
}
phi[i * prime[j]] = phi[i] * prime[j];
}
}
}
莫比乌斯筛
这个比较简单,就不写了
inline void get_euler(int n){
phi[1]=1;
for(int i=2;i<=n;i++){
if(!st[i]){
mu[i]=-1
phi[i]=i-1;
prime[++cnt]=i;
}
for(int j=1;prime[j]*i<=n && j<=cnt;j++){
st[prime[j]*i]=true;
if(i%prime[j]==0){
phi[i*prime[j]]=prime[j]*phi[i];
break;
}
mu[i*prime[j]]=-mu[i];
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
杜教筛
杜教筛用来处理形如 \(S(n)=\sum_{i=1}^nf(i)\),且 \(f(i)\) 是积性函数的式子
首先我们设 \(S(i)\) 表示 \(\sum_{x=1}^if(x)\)
因此
分解质因数
试除法
用于单个数检验是否为质数
原理:从1枚举到\(\sqrt n\)观察是否有数能被n整除
void prime(int x){
int n=x;
for(int i=2;i*i<=n;i++){
if(x%i==0)
while(n%i==0)
vec[x].push_back(i),n/=i;
}
if(n) vec[x].push_back(n);
}
Miller-Rabin
用法:\(O(k\log^2n)\) 判断 \(n\) 是否是质数。其中 \(k\) 是枚举底数的个数,\(2^{78}\) 以内只需要枚举 \(12\) 个。
费马小定理:
若 \(p\) 是质数且 \(p \nmid a\)
我们可以根据费马小定理得出一种检验素数的思路(Fermat 素性测试):
它的基本思想是不断地选取在 \([2,n)\) 中的 \(a\),并检验是否每次都有 \(a^{n−1}\equiv 1 \pmod n\)
但是很遗憾,费马小定理的逆定理并不成立
卡迈克尔数:如果有一个合数 \(n\) 满足任何一个 \(a\) 都满足 \(a^{n−1}\equiv 1 \pmod n\),那么我们称这个合数 \(n\) 为卡迈克尔数,同时,满足 \(m=2^n-1\) 那么 \(m\) 还是卡迈克尔数,所以卡迈克尔数是无穷的
二次探测定理:
若 \(p\) 是奇素数,则 \(x^2 \equiv 1 \pmod p\) 的解为 \(x=1\) 或 \(x=p-1\) \(\pmod p\)
算法流程:
(1)对于偶数和 0,1,2 可以直接判断。
(2)设要测试的数为 \(x\),我们取一个较小的质数 \(a\),设 \(s,t\),满足\(2^s\times t=x-1\) (其中 \(t\) 是奇数)。
(3)我们先算出 \(a^t\),然后不断地平方并且进行二次探测(进行 \(s\) 次)。
(4)最后我们根据费马小定律,如果最后 \(a^{x-1}\not\equiv 1 \pmod x\),则说明 \(x\) 为合数。
(5)多次取不同的 \(a\) 进行 \(Miller-Rabin\) 素数测试,这样可以使正确性更高
备注:
(1)我们可以多选择几个 \(a\),如果全部通过,那么 \(x\) 大概率是质数。
(2)\(Miller-Rabin\) 素数测试中,“大概率”意味着概率非常大,基本上可以放心使用。
(3)当 \(a\) 取前12个素数时,可以证明 \(2^{78}\) 范围内的数不会出错。
(5)另外,如果是求一个 \(\text{long long}\) 类型的平方,可能会爆掉,因此有时我们要用快速乘,不能直接乘。
\(\text{Pollard-Rho}\) 先咕了
裴蜀定理
对于二元一次方程 \(ax+by=c\),有整数解的充要条件是 \(\gcd(a,b) \mid c\)。
推论:当 \(ax+by=1\) 时,当且仅当 \(\gcd(a,b)=1\) 时有解。
证明:
设 \(d=\gcd(a,b)\) 则 \(d \mid a,d\mid b\)。由整除的性质 \(\forall x,y\in Z\),有 \(d \mid (ax+by)。\)
设 \(s\) 为 \(ax+by\) 最小正值,令 \(q=\left\lfloor \dfrac{a}{s} \right\rfloor\)。
则 \(r=a\pmod s=a-q(ax+by)=a(1-qx)+b(-qy)\)。
可见 \(r\) 也为的线性组合。
由于 \(r\) 为 \(a\pmod s\) 所得,所以 \(0\leq r<s\)。
由于 \(s\) 为线性组合的最小正值,可知。
-
因此有 $ s\mid a$ ,同理 \(s\mid b\) ,因此,\(s\) 是 \(a\) 与 \(b\) 的公约数,所以 \(d\ge s\)。
因为 \(d\mid a\) ,\(d\mid b\) ,且 \(s\) 是 \(a\) 与 \(b\) 的一个线性组合,所以由整除性质知 \(d\mid s\)。
-
但由于 \(d\mid s\) 和 \(s>0\),因此 \(d\le s\)。
由 1,2 得 \(d=s\) ,命题得证。
exgcd
现在我们对于 \(ax+by=c\) 想要获得一组整数解。
首先 \(c\) 肯定是要满足 \(\gcd(a,b) \mid c\) 的(要不然裴蜀定理白证明了)。
然后我们可以直接求 \(a_1x+b_1y=\gcd(a_1,b_1)\) 的一组整数解,最后 \(x,y\) 再乘上 \(c/\gcd(a_1,b_1)\) 即可
好了,我们现在说怎么求解。
当 \(b=0\) 时,显然 \(x=1,y=0\)
当 \(b\not= 0\) 时,有:
\(ax+by=\gcd(a,b)\)
\(\because\gcd(b,a\bmod b)=\gcd(a,b)\)
\(\therefore a x + b y = \gcd ( a , b ) = \gcd ( b , a \bmod b ) = b \times t x + ( a \bmod b ) \times t y\)
\(\because a \bmod b=a- \left\lfloor \dfrac{a}{b} \right\rfloor\times b\)
\(\therefore a x+b y=b\times tx+(a- \left\lfloor \dfrac{a}{b} \right\rfloor\times b)\times ty=a\times ty+b\times(tx−\left\lfloor \dfrac{a}{b} \right\rfloor\times ty)\)
\(\therefore x=ty,y=tx-\left\lfloor \dfrac{a}{b} \right\rfloor\times ty\)
此时我们容易发现: \(x\) 的一组解为 \(ty\),\(y\) 的一组解是 \(tx-\lfloor \dfrac a b \rfloor ty\),都被转化成了两个更小的数,这两个解可以从 \(b \times t x + ( a \bmod b ) \times t y\) 中求解,当边界达到 \(b = 0\) 时,这道题就可以解决了
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#define ll long long
using namespace std;
ll exgcd(ll a, ll b, ll& x, ll& y) {
if (!b) {
x = 1;
y = 0;
return a;
} else {
ll tx, ty;
ll d = exgcd(b, a % b, tx, ty);
x = ty;
y = tx - (a / b) * ty;
return d;
}
}
ll a, b, k, x, y;
int main() {
scanf("%lld%lld%lld", &a, &b, &k);
ll d = exgcd(a, b, x, y);
if (k % d) {
puts("no solution!");
return 0;
}
else {
x = x * k / d;
y = (k - a * x) / b;
}
printf("%lld %lld\n", x, y);
return 0;
}
欧拉定理
证明:
设 \(x_1,x_2,\dots,x_{\varphi(m)}\) 是 \([1,m]\) 里面与 \(m\) 互质的数,由于在 \(\bmod m\) 意义下两两不同且余数都与 \(m\) 互质
因此我们推理:\(ax_i\) 必定也是 \(\bmod m\) 意义下两两不同且余数都与 \(m\) 互质的数
所以:
拓展欧拉定理
推理:[Oi Wiki](欧拉定理 & 费马小定理 - OI Wiki)
乘法逆元
定义:若 \(ax\equiv 1\pmod b\) 且 \(a\) 与 \(b\) 互质,那么我们就能定义 \(x\) 为 \(a\) 的逆元,记为 \(a^{-1}\) ,所以我们也能称 \(x\) 为 \(a\) 在 \(\pmod b\) 意义下的倒数,此时我们对于 \(\dfrac{a}{b}~\pmod p\),我们就可以求出 \(b\) 在 \(\pmod p\) 意义下的逆元,来代替 \(\dfrac{1}{b}\)
快速幂
由费马小定理:若 \(p\) 为素数,\(a\) 为正整数,且 \(a\) 、\(p\) 互质。则有 \(a^{p-1}\equiv 1\pmod p\)
所以
所以我们用快速幂算出来 \(a\times b^{p-2}\) 就有 \(\dfrac{a}{b}\) 的逆元的值了
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
int mod;
ll power(ll k, ll p) {
ll ans = 1;
while (p) {
if (p & 1)
ans = ans * k % mod;
k = k * k % mod;
p >>= 1;
}
return ans;
}
ll a, b;
int main() {
scanf("%lld%lld", &a, &mod); //算a的逆元
printf("%lld", a * power(b, mod - 2) % mod);
return 0;
}
拓展欧几里得
求解 \(ax\equiv c \pmod b\) 中 \(c=1\) 的情况。我们可以转化为求解 \(ax+by=1\) 的解
所以:
ll exgcd(ll a, ll b, ll& x, ll& y) {
if (!b) {
x = 1;
y = 0;
return a;
} else {
ll tx, ty;
ll d = exgcd(b, a % b, tx, ty);
x = ty;
y = tx - (a / b) * ty;
return d;
}
}
int a, p, x, y;
int main() {
scanf("%d%d", &a, &p);
int d = exgcd(a, p, x, y);
x = (x % p + p) % p;
}
线性求逆元
设 \(p=kx+r\)
容易得到:\(k = \lfloor \dfrac p x\rfloor\),\(r = p\bmod x\)
那么我们很容易发现:\(kx+r\equiv 0\pmod p\)
此时,我们左右同时乘上 \(x^{-1}r^{-1}\) 可得
\(kr^{-1}+x^{-1}\equiv 0\pmod p\)
\(\therefore x^{-1}\equiv -kr^{-1}\pmod p\)
把 \(k=\lfloor \dfrac{p}{x} \rfloor\),\(r=p \bmod x\) 代入,得
\(x^{-1}\equiv -\left\lfloor \dfrac{p}{x} \right\rfloor \times (p \bmod x)^{-1} \pmod p\)
阶乘求逆元
首先,有如下的一个关系:
\(inv_{i+1}=\dfrac{1}{(i+1)!}\)
\(inv_{i+1}*(i+1)=\dfrac{1}{i!}\times \dfrac{1}{i+1}\times (i+1)=\dfrac{1}{i!}=inv_{i!}\)
所以我们可以先求出 \(n\) 的逆元,然后逆推即可
同时,我们也可以发现 \(\dfrac{1}{i}\) 的逆元就是:\(\dfrac{1}{i!}\times (i-1)!\)
Lucas
定理:
inline int lucas(int a, int b, int p) {
if (a < p && b < p)
return C(a, b, p);
return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
中国剩余定理(CRT)
定理:对于下列一些式子的整数求出符合条件的最小的正整数 \(x\)
首先,若\((m_1,m_2\dots m_n)\)两两互质
我们即可直接令 \(M=m_1\times m_2\dots\times m_n\)
则令 \(M_i=\dfrac{M}{m_i}\)
当 \(x\) 满足 \(x = x_1\times M_1\times M_1^{-1}+x_2\times M_2\times M_2^{-1}\dots\) 时
一定符合上面的式子
莫比乌斯反演
形式一:
证明:
我们容易发现:对于右边的式子 \(\sum_{i\mid x}g(i) \sum_{d\mid \frac x i} \mu(d)\)
结合莫比乌斯函数刚才推的性质2,我们很容易得到该式 \(=f(x)\)
得证
或者我们直接用卷积的方法证明:
原式即证:
我们让左边的那个式子的左右两边同时卷上 \(\mu\)
得:
得证
形式二:
多项式
快速傅里叶变换(FFT)
复数
设 \(a,b\) 为实数,\(i^2=-1\),形如 \(a+bi\) 的数叫复数,其中 \(i\) 被称为虚数单位,复数域是目前已知最大的域
在复平面中,\(x\) 代表实数,\(y\) 轴(除原点外的点)代表虚数,从原点 \((0,0)\) 到 \((a,b)\) 的向量表示复数 \(a+bi\)
模长:从原点 \((0,0)\) 到点 \((a,b)\) 的距离,即 \(\sqrt{a^2+b^2}\)
幅角:假设以逆时针为正方向,从 \(x\) 轴正半轴到已知向量的转角的有向角叫做幅角
计算:平行四边形法则(其实就是分配律),注意这里的 \(i^2\) 为 \(-1\):
几何定义:复数相乘,模长相乘,极角相加
这里放一张图促进理解:

模长就是 \(\sqrt{a^2+b^2}\),极角就是 \(\theta\)
代数计算方法:\((a+bi)\times (c+di)=ac+bdi^2+bci+adi=ac-bd+(bc+ad)i\)
多项式表示法
系数表示法:
设 \(A(x)\) 表示一个\(x-1\) 次多项式
则 \(A(x)=\sum_{i=0}^{n} a_i * x^i\)
例如:\(A(3)=2+3\times x+x^2\)
利用这种方法计算多项式乘法复杂度为 \(O(n^2)\)
(第一个多项式中每个系数都需要与第二个多项式的每个系数相乘)
利用这种方法计算多项式乘法的时间复杂度为 \(O(n^2)\)
点值表示法
将 \(n\) 互不相同的 \(x\) 带入多项式,会得到 \(n\) 个不同的取值 \(y\)
则该多项式被这 \(n\) 个点 \((x_1,y_1),(x_2,y_2)\dots(x_n,y_n)\) 唯一确定
其中 \(y_i=\sum_{j=0}^{n-1} a_j\times x_i^j\)
例如:上面的例子用点值表示法可以为 \((0,2)~(1,5)~(2,12)\)
利用这种方法计算多项式乘法的时间复杂度仍然为 \(O(n^2)\)
可以发现,大整数乘法复杂度的瓶颈可能在“多项式转换成点值表示”这一步(以及其反向操作),只要完成这一步就可以 \(O(n)\) 求答案了。
单位根
定义
在后面我们默认 \(n\) 为 2 的整数次幂
在复平面上,以原点为圆心,1为半径作圆,所得的圆叫单位圆。以圆点为起点,圆的 \(n\) 等分点为终点,做 \(n\) 个向量,设幅角为正且最小的向量对应的复数为 \(\omega_n\),称为 \(n\) 次单位根。
根据复数乘法的运算法则,其余 \(n-1\) 个复数为 \(\omega_n^2,\omega_n^3\ldots\omega_n^n\)
计算它们的值,我们可以用欧拉公式:\(\omega_{n}^{k}=\cos\ k *\dfrac{2\pi}{n}+i\sin k*\dfrac{2\pi}{n}\)
单位根的幅角为周角的 \(\dfrac{1}{n}\)
在代数中,若 \(z^n=1\),我们把 \(z\) 称为 \(n\) 次单位根
单位根的性质与反演
单位根的性质:
- \(\omega _n ^k =\cos~k\dfrac{2\pi}{n}+i\times \sin~k\dfrac{2\pi}{n}\)
- \(\omega _{2n}^{2k}=\omega _n^k\)
- \(\omega_n^{k+\frac{n}{2}}=-\omega _n^k\)
- \(\omega_n^0=\omega _n^n=1\)
- \((\omega _n^k)^2=\omega_n^{2k}\)
第二条的证明(如果看成一个复数,就可以发现实际上这个数没有变化):
\(\omega ^{2k}_{2n}=\cos ~2k\dfrac{2\pi}{2n}+i\sin2k\dfrac{2\pi}{2n}\)
约分后就和原来一样了
第三条的证明(如果把它看成一个复数,就可以理解成实数域和虚数域都取反了):
单位根反演:
证明:
当\(~k\mid n\) 时: 由 \(\omega_n^0=\omega_n^n~~~\) 得:\(\omega_n^{ik}=1\) 故原式等于1
当 \(k\nmid n\) 时: 原式乘上 \(\omega_n^k\) 可化成
②减①得:
易得上式为0
complex
C++的STL提供了复数模板!
头文件:#include <complex>
定义: complex<double> x;
运算:直接使用加减乘除
为什么要使用单位根作为\(x\)代入
规定我们带入的点值为 \(n\) 个单位根
设 \((y_0,y_1,y_2\dots y_{n-1})\) 为多项式 \(A(x)\) 的离散傅里叶变换(即把 \(\omega_n^0,\omega_n^1\dots\omega_n^{n-1}\) 代入上式后的结果)
我们再设一个多项式 \(B(x)\) 其各位系数为上述的 \(y\)
现在,我们把上述单位根的倒数,即 \(\omega_n^{-1},\omega_n^{-2}\dots\omega_n^{-n}\) 代入 \(B(x)\) 得 \((z_0,z_1\dots z_{n-1})\),那么有
最下面括号里的式子 \(\sum_{j=0}^{n-1}(\omega_n^{j-k})^i\) 显然是能求的
当 \(k=j\) 时,该式为 \(n\)
当 \(k\ne j\) 时
通过等比数列求和可以得出
所以我们有
因此我们可以发现:
把多项式\(A(x)\)的离散傅里叶变换结果作为另一个多项式\(B(x)\)的系数,取单位根的倒数即 \(\omega ^0_n,\omega ^{−1}_n,\omega ^{−2}_n,...,\omega ^{-(n−1)}_n\)作为 \(x\) 代入 \(B(x)\),得到的每个数再除以 \(n\),得到的就是 \(A(x)\) 的各项系数
离散傅里叶变换(DFT)的数学证明
我们考虑把一个普通的多项式按奇偶性分类,有:
所以我们设成两个多项式:
\(A_1(x)=a_0+a_2x+a_4x^2+⋯+a_{n−2}x^{\frac{n}{2}-1}\)
\(A_2(x)=a_1+a_3x+a_5x^2+⋯+a_{n−1}x^{\frac{n}{2}-1}\)
因此\(A(x)=A_1(x^2)+xA_2(x^2)\)
假设当前\(k<\frac{n}{2}\),现再我们要代入 \(x=\omega_n^k\)
我们再代入 \(x=\omega_n^{k+\frac{n}{2}}\)
因此,只要我们求出 \(A_1(x)\) 和 \(A_2(x)\) 分别在 \(\omega_{\frac{n}{2}}^0,\omega_{\frac{n}{2}}^1,\omega_{\frac{n}{2}}^2\dots\omega_{\frac n 2} ^{\frac n 2}\) 等的点值表示,就可以 \(O(n)\) 的求出 \(A(\omega_n^{1\sim\frac n 2})\) 的点值表示,同时可以得到 \(A(\omega_n^{\frac n2 + 1\sim n})\),正好 \(n\) 个,每个 \(A_1\) 和 \(A_2\) 也这么求,持续分治,分治的边界是 \(n=1\)
另外一边我们是离散傅里叶逆变换(IDFT) 也就这么理解就行了
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int MAXN = 2e6 + 10;
inline int read() {
char c = getchar(); int x = 0, f = 1;
while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}
return x * f;
}
const double Pi = acos(-1.0);
struct complex {
double x, y;
complex (double xx = 0, double yy = 0){x = xx, y = yy;}
}a[MAXN], b[MAXN];
complex operator + (complex a,complex b){ return complex(a.x + b.x, a.y + b.y);}
complex operator - (complex a,complex b){ return complex(a.x - b.x, a.y - b.y);}
complex operator * (complex a,complex b){ return complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);}
void fast_fast_tle(int len, complex *a, int type){
if (len == 1) return ;
complex a1[len >> 1], a2[len >> 1];
for (int i = 0; i <= len; i += 2) a1[i >> 1] = a[i], a2[i >> 1] = a[i | 1];
fast_fast_tle(len >> 1, a1, type);
fast_fast_tle(len >> 1, a2, type);
complex Wn = complex(cos(2.0 * Pi / len), type * sin(2.0 * Pi / len)), w = complex(1,0);
for (int i = 0; i < (len >> 1); i++, w = w * Wn)
a[i] = a1[i] + w * a2[i],
a[i + (len >> 1)] = a1[i] - w * a2[i];
}
int main(){
int N = read(), M = read();
for (int i = 0; i <= N; i++) a[i].x = read();
for (int i = 0; i <= M; i++) b[i].x = read();
int len = 1;
while (len <= N + M) len <<= 1;
fast_fast_tle(len, a, 1);
fast_fast_tle(len, b, 1);
//type为1表示从系数变为点值
//-1表示从点值变为系数
for (int i = 0; i <= len; i++) a[i] = a[i] * b[i];
fast_fast_tle(len, a, -1);
for (int i = 0;i <= N + M; i++) printf("%d ",(int)(a[i].x / len + 0.5));//按照我们推导的公式,这里还要除以n
return 0;
}
优化 FFT
递归优化
在进行 \(\text{fft}\) 时,我们要把各个系数不断分组并放到两侧,那么一个系数原来的位置和最终的位置有什么规律呢?
初始位置:0 1 2 3 4 5 6 7
第一轮后:0 2 4 6|1 3 5 7
第二轮后:0 4|2 6|1 5|3 7
第三轮后:0|4|2|6|1|5|3|7
用|隔开各组数据
我们把二进制拉出来,发现一个位置a上的数,最后所在的位置是a二进制翻转得到的数
那么我们可以据此写出非递归版本 \(\mathrm{FFT}\):先把每个数放到最后的位置上,然后不断向上还原,我们每次把相邻的两块共同贡献给上面的那一块,同时求出点值表示。
蝴蝶操作
貌似也没啥,就是把东西先存上再用,感觉直接看模板就懂了,差不多得了,还是直接背吧
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
const int mod = 1e9 + 7;
const int N = 3e6 + 5;
const double Pi = acos(-1.0);
int n, m, T, L, lim, rev[N];
struct cp {
double x, y;
cp() {x = 0, y = 0;}
cp(double a, double b) {x = a, y = b;}
}f[N], g[N], ans[N];
cp operator + (cp a, cp b) {return cp(a.x + b.x, a.y + b.y);}
cp operator - (cp a, cp b) {return cp(a.x - b.x, a.y - b.y);}
cp operator * (cp a, cp b) {return cp(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);}
inline void FFT(cp *a, int type) {
rep (i, 0, lim - 1) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int len = 1; len < lim; len <<= 1) {
cp wn(cos(Pi / len), sin(Pi / len) * type);
for (int i = 0; i < lim; i += (len << 1)) {
cp w(1, 0), x, y;
rep (j, 0, len - 1) {
x = a[i + j], y = w * a[i + j + len];
a[i + j] = x + y, a[i + j + len] = x - y;
w = w * wn;
}
}
}
}
int main(){
read(n, m);
for (lim = 1; lim <= n + m; lim <<= 1) L++;
rep (i, 0, n) read(f[i].x);
rep (i, 0, m) read(g[i].x);
rep (i, 0, lim - 1) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (L - 1));
FFT(f, 1);
FFT(g, 1);
rep (i, 0, lim) ans[i] = f[i] * g[i];
FFT(ans, -1);
rep (i, 0, n + m) write((int)(ans[i].x / lim + 0.5), ' ');
return 0;
}
//write:RevolutionBP
NTT
阶
设 \(r,n\) 是互素的整数, \(r \not = 0\) ,\(n>0\) ,使得 \(r^x\equiv 1 \pmod n\) 成立的最小正整数
\(x\) 称为 \(r\) 模 \(n\) 的阶,标为 \(\delta _n r\)
原根
如果 \(r,n\) 都是互素的正整数,当 \(\text{ord}_nr=\varphi(n)\) 时,称 \(r\) 是模 \(n\) 的原根,即 \(r\) 是 \(n\) 的原根
我们令 \(n\) 为大于 \(1\) 的 \(2\) 的幂,\(p\) 为素数且 \(n \mid (p-1)\),\(g\) 为 \(p\) 的一个原根
我们设
所以
我们发现,原根包含着单位根的所有性质,所以我们就可以用原根代替单位根
最大优点:保持精度不变
特殊记忆:\(998244353\) 的原根是 \(3\) 和 \(114514\)
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
const int mod = 998244353;
const int N = 5e6 + 5;
const int G = 114514;
const double Pi = acos(-1.0);
#define int long long
int n, m, T, b, lim, rev[N], f[N], g[N], ans[N];
const int invG = power(G, mod - 2);
inline void FFT(int *a, int type) {
rep (i, 0, lim - 1) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int len = 1; len < lim; len <<= 1) {
int wn = power(type == 1 ? G : invG, (mod - 1) / (len << 1));
for (int i = 0; i < lim; i += (len << 1)) {
int w = 1, x, y;
rep (j, 0, len - 1) {
x = a[i + j], y = 1ll * w * a[i + j + len] % mod;
a[i + j] = (x + y) % mod, a[i + j + len] = (x - y + mod) % mod;
w = 1ll * w * wn % mod;
}
}
}
if (type == 1) return ;
int inv = power(lim, mod - 2);
rep (i, 0, lim) a[i] = a[i] * inv % mod;
}
signed main(){
read(n, m);
for (lim = 1; lim <= n + m; lim <<= 1);
rep (i, 0, n) read(f[i]);
rep (i, 0, m) read(g[i]);
rep (i, 0, lim - 1) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) * (lim >> 1));
FFT(f, 1), FFT(g, 1);
rep (i, 0, lim) ans[i] = f[i] * g[i];
FFT(ans, -1);
rep (i, 0, n + m) write(ans[i], ' ');
return 0;
}
//write:RevolutionBP
多项式乘法逆
题目描述
给定一个多项式 \(F(x)\) ,请求出一个多项式 \(G(x)\), 满足 \(F(x)*G(x)\equiv 1\pmod{x^n}\)。系数对 \(998244353\) 取模。
首先,若 \(x\) 只有 \(1\) 项时,我们的 \(G(x)\) 就是 \(x\) 的逆元,不然的话,我们就可以递归求解
我们假设当前已知:
由于
显然:
两式相减,我们就可以得到:
左右同时把 \(F(x)\) 去掉,则有
然后我们左右同时平方可以发现:
拆开后有:
再给两边乘上 \(F(x)\),化简
我们发现已经用 \(H(x)\) 和 \(F(x)\) 来代替 \(G(x)\) 了。
然后我们递归去找 \(H(x)\) 就行
inline void Inv(ll *X, ll *Y, ll len) {
if (len == 1) return Y[0] = inv(X[0]), void();
Inv(X, Y, (len + 1) >> 1);
for (lim = 1; lim < (len << 1); lim <<= 1);
static ll H[N];
rep (i, 0, len - 1) H[i] = X[i];
rep (i, len, lim - 1) H[i] = 0;
NTT(H, 1, lim), NTT(Y, 1, lim);
rep (i, 0, lim)
Y[i] = ((2ll - Y[i] * H[i] % mod) + mod) % mod * Y[i] % mod;
NTT(Y, -1, lim);
rep (i, len, lim - 1) Y[i] = 0;
}
多项式对数函数(多项式 ln)
题目描述
给出 \(n-1\) 次多项式 \(F(x)\) ,求一个 \(\bmod x^n\) 下的多项式 \(G(x)\),满足 \(G(x)\equiv \ln F(x)\pmod {x^n}\)
首先,我们令 \(f(x)=\ln(x)\)
则原式可化为 \(G(x)\equiv f(F(x))\pmod{x^n}\)
我们对两边同时求导有:
\(G'(x) \equiv f'(F(x))F'(x) \pmod {x^{n-1}}\)
由于 \(\ln'(x)=\dfrac{1}{x}\)
\(G'(x)\equiv\dfrac{F'(x)}{F(x)} \pmod{x^{n-1}}\)
那么我们此时再积回去,得到最终式子
至于积分和求导的求解,直接看就行
求导公式
积分公式
inline void Direv(int *A, int *B, int len) { //求导
for (int i = 1; i < len; ++i) B[i - 1] = mul(A[i], i); B[len - 1] = 0;
}
inline void Inter(int *A,int *B,int len){ //积分
for(int i = 1; i < len; ++i) B[i] = mul(A[i - 1], ksm(i, P - 2)); B[0] = 0;
}
void Ln(int *a, int *b, int len) {
Direv(a, A, len), Inv(a, B, len);int l = len << 1;
NTT(A, 1, l), NTT(B, 1, l);
for (int i = 0; i < l; ++i) A[i] = mul(A[i], B[i]);
NTT(A, -1, l), Inter(A, b, len);
}
多项式开根
题目描述
给定一个 \(n-1\) 次多项式 \(A(x)\) ,在 \(\bmod x^n\) 意义下的多项式 \(B(x)\) ,使得 \(B^2(x)\equiv A(x) \pmod {x^n}\)。若有多解,请取零次项系数较小的作为答案。
这个和上面那个差不多吧,顶多就是换个推导过程
假设我们已知:
易知:
我们继续推导可得:
由于题目要求0次项系数最小的最为答案,所以
直接进行多项式求逆和NTT即可
t{A_0}=1$
泰勒展开
看了知乎上一个回答,倒是蛮有趣的

首先对于这个函数,我们定义它为 \(f(x)\)
我们现在想做的就是构造一个函数 \(g(x)\) 和它亿分相似
首先我们就要找一个点和它重合,哪个点呢?显然 \((0,1)\) 是最好的选择
然后我们就会选择在 \((0,1)\) 处进行 \(n\) 阶求导,然后找到一个函数 \(g(x)\) 使得这 \(p(p\in [1,n])\) 阶的导数全部和 \(f(x)\) 的 \(p\) 阶导数相同,然后我们会考虑,可能一次两次的,我们愿意算,但是太多了肯定就不愿意了,所以这个 \(g(x)\) 得长得靠谱,还得好算
所以我们有了一个绝妙的主意,我们用多项式来代替,众嗦粥之,众所周知,我们的 \(n\) 次多项式 \(n\) 阶求导以后可是个常数啊,这一点就会非常好用
这里的图引自知乎,第一条回答(号主已经把号注销了,所以我也没法确认,如有侵权希望可以和我私聊)
满足二阶导数时,我们的图长这样
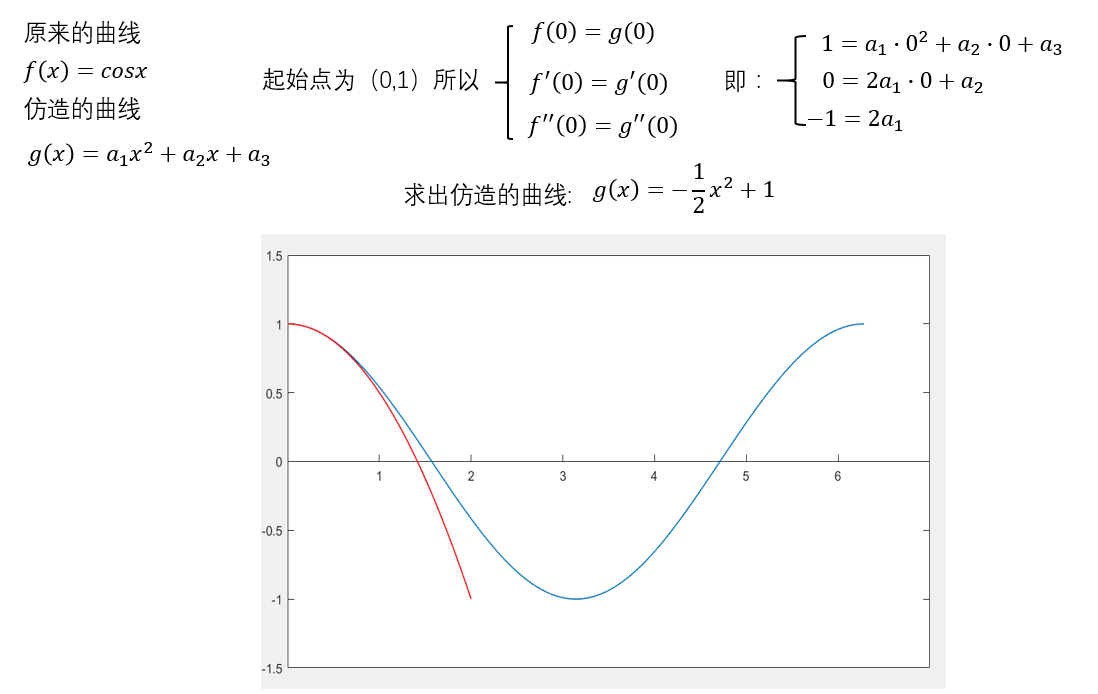
满足四阶导数时,我们的图长这样
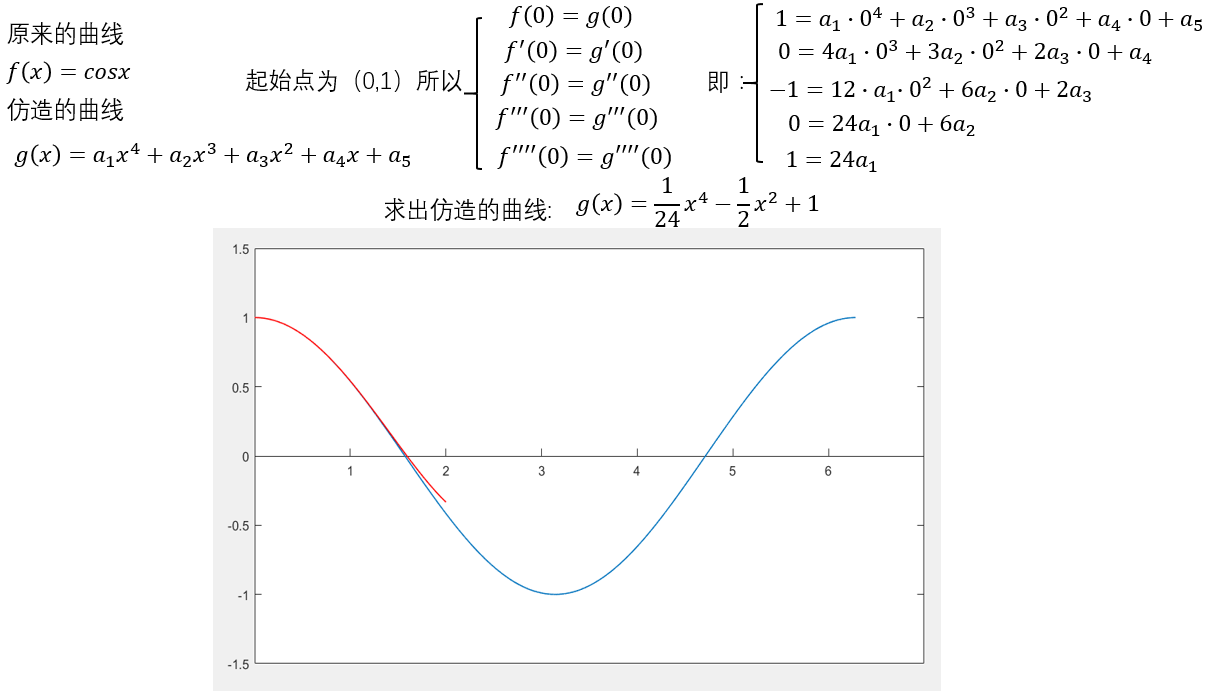
很容易想到,如果我们的函数无穷次求导以后,这两个函数就会无限接近
比如说我们要求 \(\cos 2\),这很难求,但是我们肯定知道 \(\cos \dfrac \pi 2\) 的值,那么直接进行一个很多次的求导,然后在我的构造函数上就能找到近似值
那么我们考虑能不能直接用代数式子直接推出来呢?
答案是肯定的,刚才我们说,如果我们 \(n\) 次求导以后两个函数会无限相似
首先容易得到,如果我们是 \(n\) 次求导,那么最后我们得到的式子长这样
首先容易得到 \(a_0=g(0)=f(0)\)
当 \(g^n(x)\) 时,原式长成 \(n!a_n\)。
容易得到: \(g^n(0)=f^n(0)=n!a_n\)
所以
综上:
若我们不是从 \((0,f(0))\) 开始的,而是从 \((x_0,f(x_0))\) 开始的,那么这个式子改一改就有了
在 \(\mathrm{OI}\) 中,我们很多东西都是有精度限制的,请问我们这个式子什么时候才能算到我们要的误差之内呢?
首先我们发现,我们的式子是越来越小的,原因我们可以这样理解
泰勒展开是先把函数的大框架构建完毕,然后精细化的过程,所以你后面的是基于前面的框架搭建的所以是越来越小,越来越精细的过程
我们会发现,其实我们的式子可远不止这些,我们后面的式子可以无限拉长,类似这样:
假设现在我们把 \(g\) 精确到 \(n\) 阶了, 那么后面的那一堆就是误差项,有一个叫佩亚诺的倒霉蛋试着去化简这个误差项,结果后来啥也没搞出来,不过他用后面的和前面做了个商,算出来了一个东西,不够为了纪念他,我们还是将这个误差项叫作佩亚诺余项
他算了个这玩意:
然后就是两位天才的故事拉格朗日和柯西
首先是一个简单的问题,给你一段时间内汽车走过的路程与时间的关系(\(ST\) 图像),然后我告诉你平均速度是 \(v_1\),然后还告诉你其中某一点的速度是 \(v_0<v_1\),那么我们很容易知道一定会出现一个点的速度 \(v_2\) 使得 \(v_2>v_1\)
然后这个叫拉格朗日的神仙就直接把这个写成了一个方程,我们称其为拉格朗日中值定理:
然后柯西拓展了一下,变成了柯西中值定理
然后我们回归原来我们的误差项等一系列定义
设
我们设 \(T(x)=(x-x_0)^{n+1}\),且 \(T(x_0)=R(x_0)=0\)
我们让等式两边同时除以 \(T(x)\),并且使用柯西中值定理,有
然后我们很容易发现,我们仿照刚才的方式容易得到,上面的那个玩意可以无穷次求导,并且长得和我们刚才的 \(R(x)\) 除了每一项前面加了个系数 \((n+y)\) 以外都一样,下面的话也是,并且下面除去 \((n+1)\) 以外也一样,分开写出来
分子:
所以
于是我们可以设 \(P(\xi)=R^{'}(\xi)\) 且 \(P(x_0)=0\)
分母:
我们可以直接设 \(Q(\xi)=T^{'}(\xi)\),且 \(Q(x_0)=0\)
发现原式变成了 \(\dfrac {P(\xi)} {Q(\xi)}\),很巧合我们可以继续用柯西中值定理归纳
很容易发现我们可以一直这样归纳最终的结果就会是
这样的话就非常非常非常好了,我们不用让 \(x\) 趋近于 \(x_0\),直接就能算出一个点的误差值
老实说,后面的这一堆东西我们一般也就数学分析的时候用,OI中还是泰勒展开直接应用比较多,原因是生成函数等对于 \(x^n\) 是无效的,所以我们不用考虑这么多,直接套公式使用即可
牛顿迭代
牛顿迭代就是说,我们给定一个连续的函数 \(f(x)\),然后我们随便找它上面的一个点,然后作切线,发现这个切线会和 \(x\) 轴有一个交点,然后我们以这个交点作垂线,交函数上一个点,然后 继续上述操作,我们最终会发现我们的这个和 \(x\) 轴的交点会无限逼近 \(f(x)\) 和 \(x\) 轴的交点
代数方法说明的话就是我们设刚开始函数上这个交点是 \((x_n,f(x_n))\),那么和 \(x\) 轴交在了 \((x_{n+1},0)\)。我们重复这个过程,如下图

而且我们顺带说一下切线方程:我们如果已知 \(f(x)=kx+b\),那么我们的 \(k\) 可以用导数表示出来,即 \(f(x)=f^{'}(x)+b\) 我们称其为切线方程,对于刚才这个玩意我们也可以用类似这种方式解决,我们要求 \(x_{n+1}\) 的值,即求 $f(x_n)+f^{'}(x_n)\times(x_{n+1}-x_n)=0 $,我们搞一搞:
同理我们把横坐标及函数转化成多项式形式,就有 :
多项式指数函数(多项式 exp)
题目描述
给出 \(n-1\) 次多项式 \(A(x)\),求一个 \(\bmod x^n\) 下的多项式 \(B(x)\),满足 \(B(x)\equiv e^{A(x)}\)。系数对 \(998244353\) 取模
首先对于两边同时取 \(\ln\),没什么好说的
我们令 \(F(G(x))=\ln B(x)- A(x)\equiv 0\pmod {x^n}\)
并且我们容易得到:
代入牛顿迭代以后得到:
化简后得:
到这里,最简单的多项式已经都有了,剩下的也是这些的拓展和加深,所以我们可以放出vector封装好的多项式模板了
/*
Blackpink is the Revolution
light up the sky
Blackpink in your area
*/
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cctype>
#include <bitset>
#include <vector>
#include <cstdio>
#include <cmath>
#include <queue>
#include <ctime>
#include <map>
#include <set>
using namespace std;
using ll = long long;
using P = pair<int ,int>;
using poly = vector <ll>;
namespace scan {
template <typename T>
inline void read(T &x) {
x = 0; char c = getchar(); int f = 0;
for (; !isdigit(c); c = getchar()) f |= (c == '-');
for (; isdigit(c); c=getchar()) x = x * 10 + (c ^ 48);
if (f) x = -x;
}
template <typename T, typename ...Args>
inline void read(T &x, Args &...args) {
read(x), read(args...);
}
template <typename T>
inline void write(T x, char ch) {
if (x < 0) putchar('-'), x = -x;
static short st[30], tp;
do st[++tp] = x % 10, x /= 10; while(x);
while (tp) putchar(st[tp--] | 48);
putchar(ch);
}
template <typename T>
inline void write(T x) {
if (x < 0) putchar('-'), x = -x;
static short st[30], tp;
do st[++tp] = x % 10, x /= 10; while(x);
while(tp) putchar(st[tp--] | 48);
}
inline void write(char ch){
putchar(ch);
}
template <typename T, typename ...Args>
inline void write(T x, char ch, Args ...args) {
write(x, ch), write(args...);
}
} //namespace scan
using namespace scan;
#define rep(i, a, b) for(ll i = (a); (i) <= (b); ++i)
#define per(i, a, b) for(ll i = (a); (i) >= (b); --i)
const ll mod = 998244353;
const ll inv2 = 499122177;
const int N = 2e6 + 5;
ll n, m, T;
namespace Poly {
#define Size(_) int(_.size())
#define lg(x) ((x) == 0 ? -1 : __lg(x))
const ll Primitive_Root = 114514;
const ll invPrimitive_Root = 137043501;
poly rev;
inline ll qpow(ll x, ll k) {
ll res = 1;
while (k) {
if (k & 1) res = res * x % mod;
x = x * x % mod;
k >>= 1;
}
return res;
}
inline ll inv(ll x) {return qpow(x, mod - 2);}
inline void NTT(ll *a, ll lim, ll type) {
rev.resize(lim);
rep (i, 0, lim - 1) {
rev[i] = rev[i] = (rev[i >> 1] >> 1) | ((i & 1) * (lim >> 1));
if (i < rev[i]) swap(a[i], a[rev[i]]);
}
for (ll len = 1; len < lim; len <<= 1) {
ll wn = qpow(type == 1 ? Primitive_Root : invPrimitive_Root, (mod - 1) / (len << 1));
for (ll i = 0; i < lim; i += (len << 1)) {
ll w = 1, x, y;
rep (j, 0, len - 1) {
x = a[i + j] % mod, y = w * a[i + j + len] % mod;
a[i + j] = (x + y) % mod, a[i + j + len] = (x - y + mod) % mod;
w = w * wn % mod;
}
}
}
if (type == 1) return ;
ll inv_len = inv(lim);
rep (i, 0, lim - 1) a[i] = a[i] * inv_len % mod;
}
poly operator * (poly F, poly G) {
ll siz = Size(F) + Size(G) - 1, lim = (1 << (lg(siz - 1) + 1));
if (siz <= 300) {
poly H(siz);
per (i, Size(F) - 1, 0)
per (j, Size(G) - 1, 0)
H[i + j] = (H[i + j] + F[i] * G[j] % mod) % mod;
return H;
}
F.resize(lim), G.resize(lim);
NTT(F.data(), lim, 1);
NTT(G.data(), lim, 1);
rep (i, 0, lim - 1) F[i] = F[i] * G[i] % mod;
NTT(F.data(), lim, -1);
F.resize(siz);
return F;
}
poly operator + (poly F, poly G) {
int siz = max(Size(F), Size(G));
F.resize(siz);
G.resize(siz);
rep (i, 0, siz - 1) F[i] = F[i] + G[i] % mod;
return F;
}
poly operator - (poly F, poly G) {
int siz = max(Size(F), Size(G));
F.resize(siz);
G.resize(siz);
rep (i, 0, siz - 1) F[i] = (F[i] - G[i] + mod) % mod;
return F;
}
poly cut(poly F, ll len) {
F.resize(len);
return F;
}
poly Direv(poly F) {
int siz = Size(F) - 1;
rep (i, 0, siz - 1) F[i] = F[i + 1] * (i + 1) % mod;
F.pop_back();
return F;
}
poly inter(poly F) {
F.emplace_back(0);
per (i, Size(F) - 1, 0) F[i] = F[i - 1] * inv(i) % mod;
F[0] = 0;
return F;
}
poly Inv(poly F) {
int siz = Size(F), lim = (1 << (lg(siz - 1) + 1));
poly G;
G.resize(1);
G[0] = inv(F[0]);
F.resize(lim);
for (int len = 2; len <= lim; len <<= 1) {
poly tmp(len << 1, 0);
rep (i, 0, len - 1) tmp[i] = F[i];
G.resize(len << 1);
NTT(tmp.data(), len << 1, 1), NTT(G.data(), len << 1, 1);
rep (i, 0, (len << 1) - 1)
G[i] = G[i] * (mod + 2ll - tmp[i] * G[i] % mod) % mod;
NTT(G.data(), (len << 1), -1);
G.resize(len);
}
G.resize(siz);
return G;
}
poly ln(poly F) {
int siz = Size(F);
return cut(inter(cut(Direv(F) * Inv(F), siz)), siz);
}
poly exp(poly F) {
int siz = Size(F);
poly G{1};
for (int i = 2; (i >> 1) < siz; i <<= 1) {
G = G * (poly{1} - ln(cut(G, i)) + cut(F, i));
G.resize(i);
}
G.resize(siz);
return G;
}
poly sqrt(poly F) {
int siz = Size(F);
poly G{1};
for (int i = 2; (i >> 1) < siz; i <<= 1) {
G = (G + (cut(F, i) * cut((Inv(cut(G, i))), i))) * poly{inv2};
G.resize(i);
}
G.resize(siz);
return G;
}
}// namespace Poly
using namespace Poly;
namespace RevolutionBP {
ll lim, L;
void main() {
read(n);
poly F(n);
for (auto& i : F) read(i);
F = Poly::sqrt(F);
for (auto& i : F) write(i, ' ');
return void();
}
}
signed main(){
RevolutionBP::main();
return 0;
}
//write: RevolutionBP
生成函数
生成函数(generating function),又称母函数,是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。
生成函数有许多不同的种类,但大多可以表示为单一的形式:
其中 \(k_n(x)\) 被称为核函数,不同的核函数会导出不同的生成函数,分成3类
普通生成函数:\(k_n(x)=x^n\) (OGF)
指数生成函数:\(k_n(x)=\dfrac {x^n} {n!}\) (EGF)
狄利克雷生成函数:\(k_n(x)=\dfrac {1} {n^x}\) (DGF)
另外,对于生成函数 \(F(x)\),我们用 \([k_n(x)]F(x)\) 来表示它的第 \(n\) 项的核函数对应的系数,也就是 \(a_n\)
容易发现其中的 \(x\) 对于原式中的结果并没有什么影响,我们想要的应该是固定项前面的系数
普通生成函数
形式:
\(a\) 既可以是有穷序列,也可以是无穷序列
若干例子:
序列 \(a=\langle 1,2,3\rangle\) 的OGF:\(1+2x+3x^2\)
序列 \(a=\langle 1,1,1,\dots,1\rangle\) 的OGF:\(\displaystyle\sum_{n} x^n\)
序列 \(a=\langle 1,2,4,8,16,\dots\rangle\) 的OGF:\(\displaystyle \sum_n 2^nx^n\)
序列 \(a=\langle 1,3,5,7,9,\dots\rangle\) 的OGF:\(\displaystyle \sum_n (2n+1)x^n\)
基本运算
考虑两个序列 \(a,b\) 的普通生成函数,分别为 \(F(x),G(x)\),那么有
因此 \(F(x)\pm G(x)\) 是序列 \(\\langle a_n\pm b_n \rangle\)
考虑乘法运算,也就是卷积:
封闭形式
这是OGF比较好玩的一个东西,就是说每次写成一个多项式真的很难受,但是如果能够把这个形式幂级数写成其它的形式可能就会好很多
对于上述例二,容易发现:
很容易想到移项后可以得到:\(F(x)=\dfrac {1}{1-x}\)
可能会有点疑惑,这个东西怎么还能是负数?
实际上发现,如果要让前面的形式幂级数在 \(\infty\) 处收敛,x的范围应在 \(\in (-1,1)\)
但是还是不需要去理它,因为我们生成函数的本质不在于这个 \(x\) 的取值,或者说对于这个封闭形式,只是一种方便推过去和推回来的过程罢了,并不是对原式的具体阐述
有若干种物品 ,每种物品只有1件,求取 \(n\) 件物品的总方案数。
每种物品的生成函数是 \(1\times x^0+1\times x^1\)
那么若干个物品乘起来就是 \((x+1)^n\)
然后用二项式定理展开一下就可以得到:
\(\displaystyle (x+1)^n=\sum_{i=0}^n \binom {n} {i}x^i\)
如果学过组合数学就会发现这个确实很对
当然也有比较恶心的
有若干种物品 ,每种物品可以取任意件,求取 \(n\) 件物品的总方案数
和上个题一样,每个物品的生成函数是:\(\displaystyle\sum_{i=0}^n x^i\) 很快就能发现,又等于 \(\dfrac 1 {1-x}\)
这样的话 \(m\) 件物品的生成函数就是
同时可以用隔板法理解,答案是相同的
来个重头戏:斐波那契数列:
前置知识:
\(\displaystyle\dfrac {1} {1-kx}=\sum_{i=0}k^ix^i\)
设 \(F(x)\) 表示斐波那契数列的生成函数
首先第一步拆分,容易得到:
容易发现下面两个相加就只和第一个差出来一个数1
\(A-xA-x^2A=1\)
整理一下:\(A=\dfrac {1}{1-x-x^2}\)
然后发现这和上面补充的前置知识太相似了,如果能做到和前面的那个完全一样就好了
然后就是很多套路性的转化了
第一个因式分解,\(1-x-x^2=(1-ix)(1-jx)\)
解得 \(i=\dfrac {1+\sqrt 5} {2}~~j =\dfrac {1-\sqrt 5} {2}\)
但是这时候还是两个 \(\dfrac {1} {1-kx}\) 的卷积,容易发现既然根式都出来了,上面的1也顺路拆了算了
令 \(ai+bj=1\),得到 \(a=\dfrac {1} {{\sqrt 5}}i~~b=-\dfrac {1} {\sqrt 5}j\)
带回原来的式子里,裂项以后拆成一个巨无霸式子:
\(A=\dfrac {i} {\sqrt 5}\dfrac {1}{1-ix}-\dfrac{j}{\sqrt 5}\dfrac{1}{1-jx}\)
写的更加简便一点:
\(\displaystyle A = \dfrac {M} {1-ax}+\dfrac {N} {1-bx}=\sum_{k=0}(Ma^k + Nb^k)x^k\)
同时 \(M=\dfrac {\sqrt 5 i} {5},N=-\dfrac {\sqrt 5 j} {5},a=i,b=j\)
然后就是前面的基本多项式运算了
\(\displaystyle F(x)=\sum_{k=0}((\dfrac {\sqrt 5 i} {5}) \times (\dfrac {1+\sqrt 5} 2)^k-\dfrac {\sqrt 5 j} {5}\times (\dfrac {1-\sqrt 5} {2})^k)x^k\)
经过一点点化简就能得到:
到这里其实要说的也就差不多了
P2000 拯救世界
为了拯救世界,小 a 和 uim 决定召唤出 kkksc03 大神和 lzn 大神。根据古籍记载,召唤出任何一位大神,都需要使用金木水火土五种五行神石来摆一个特定的大阵。而在古籍中,记载是这样的:
金神石的块数必须是 \(6\) 的倍数
木神石最多用 \(9\) 块
水神石最多用 \(5\) 块
火神石的块数必须是 \(4\) 的倍数
土神石最多用 \(7\) 块
金神石的块数必须是 \(2\) 的倍数
木神石最多用 \(1\) 块
水神石的块数必须是 \(8\) 的倍数
火神石的块数必须是 \(10\) 的倍数
土神石最多用 \(3\) 块
有多少种方案
直接列出所有的生成函数:
\(1+x^6+x^{12}+⋯=\dfrac 1 {1 − x^{6}}\)
\(1+x^2+x^{3}+⋯+x^9=\dfrac {1 − x^{10}} {1-x}\)
\(1+x^2+x^{3}+⋯+x^5=\dfrac {1 − x^{6}} {1-x}\)
\(1+x^4+x^{8}+⋯=\dfrac {1 − x^{8}} {1-x}\)
\(1+x^2+x^{4}+⋯=\dfrac 1 {1 − x^{2}}\)
\(1+x=\dfrac {1-x^2} {1 − x}\)
\(1+x^8+x^{16}+⋯=\dfrac 1 {1 − x^{8}}\)
\(1+x^{10}+x^{20}+⋯=\dfrac 1 {1 − x^{10}}\)
\(1+x+x^2+x^3=\dfrac {1-x^4} {1 − x}\)
直接全部撑起来,发现很多都能化简,最后得到了 \(\dfrac {1} {(1-x)^5}\)
根据上面得到的
直接发现第 \(n\) 项就是 \(\binom {n+4} {4}=\)\(\dfrac{(n+4)(n-3)(n-2)(n-1)} {24}\)
组合数学
加法 & 乘法原理
加法原理:
做一件事情,完成它有 \(n\) 类方式,第一类方式有 \(M_1\) 种方法,第二类方式有 \(M_2\) 种方法,\(\dots\) 第 \(n\) 类方式有 \(M_n\) 种方法,那么完成这件事情共有 \(M_1+M_2+……+M_n\) 种方法。
乘法原理:
做一件事,完成它需要分成 \(n\) 个步骤,做第一 步有 \(m_1\) 种不同的方法,做第二步有 \(m_2\) 种不同的方法,……,做第 $n $ 步有 \(mn\) 种不同的方法。那么完成这件事共有 \(N=m_1\times m_2\times m_3\times \dots\times mn\) 种不同的方法。
排列与组合基础
排列数
\(n\) 个数中任取 \(m\) 个数,考虑顺序,用 \(A_m^n\) 或者 \(P_m^n\) 表示即可,计算公式如下:
由于是排列数,可以理解成 \(n\) 个人选 \(m\) 个人出来排队,问共有多少种排队顺序
组合数
从 \(n\) 个不同元素中,任取 \(m\) 个元素组成一个集合,问有多少种集合,用 \(C_n^m\) 或者 \(\binom {n} {m}\) 表示,不过一般人应该都喜欢后面的那个,计算公式如下 :
特别规定当 \(m > n\) 时,原式为 \(0\)
二项式定理
数学归纳法很容易得到
也可以直接把 \((a+b)^n\) 直接拆开成乘积的形式,那么我们考虑 \(a^rb^{n-r}\) 的系数,就是我们在这 \(n\) 个 \(a+b\) 中,每次选一个 \(a\) 或者 \(b\),选 \(r\) 个 \(a\) 的方案数,因此就是 \(\binom n r\)
拓展为多项式形式(广义二项式定理)
组合数求和定理
三种理解方式:
第一种,我们把式子左边理解成从 \(n\) 个球里面取 \(0\) 个球,\(1\) 个球,\(\dots\),\(n\) 个球的方案,其实加起来以后就是从 \(n\) 个球中任意取的总方案数,我们把右边理解成每个球取或不取都有一种方案总共就是 \(2^n\) 种方案,很容易发现它们是等价的
第二种,用数学归纳法,很简单,不想写了
第三种,用二项式定理证明:令 \(a=b=1\) 即可直接得出
排列组合数性质和推论
具体数学中最重要的二项式系数一共给了十个,这里直接列出,还夹带了一个私货
多重集的排列数 多重集的组合数
多重集的定义:可以包含相同元素的集合
设 \(S=\{n_1\times a_1,n_2\times a_2,\dots,n_ka_k\}\),表示由 \(n_i\) 个 \(a_i\) 组成的多重集,多重集的排列数为
多重集的排列数和多重组合数是一个东西,多重集的排列数是另一个东西
多重集的组合数:我们从 \(S\) 里面选取 \(r\) (\(1\le r<n_i,\forall i\in [1,k]\))个元素组成多重集的方案数为
不相邻的排列
\(1\sim n\) 中选 \(k\) 个,这 \(k\) 个数中任何两个数不相邻的组合有 \(\displaystyle \binom {n - k + 1} k\)
我们可以理解成我们先从原来的里面抠出来 \(k-1\) 个格,使得剩下的就可以随便选了,选完以后我们把这空着的几个格移动到选取的相邻两个之间即可
错位排列
我们考虑有 \(n\) 个数,有多少种方案使得他们没有一个在正确的位置上
正解是分两种情况讨论,对于第 \(i\) 个信封来首如果前面的 \(n-1\) 个都装错了,那么第 \(n\) 个信封和前面的任意一个交换即可,如果前面的 \(n-1\) 个中有一个装对了,别的都装错了,那么我们就让第 \(n\) 个信封和那个对的交换即可
只有这两种方式可以使得一次交换以后为错排,所以我们的总方案数为
圆排列
\(n\) 个人围成一圈的排列数 \(Q_n^n\)
卡特兰数
卡特兰数用于处理这样的组合问题:我们默认一个行为是加一,另一个行为是减一,那么我们要保证前缀和恒非负即可
这样的话我们的卡特兰数可以有一个组合意义:对于一个 \(n\times n\) 的网格图,我们找到 \(y=x\) 这条线,要求从 \((0,0)\) 开始走到 \((n,n)\) 且不能超出 \(y=x\) 的路径条数
我们钦定向左走是 \(1\),向右走是 \(-1\)
首先我们不考虑 \(y=x\) 的限制,那么 \(ans = \displaystyle \binom {2n} n\)
我们考虑当不合法时,路径一定会经过 \(y=x+1\) 这条线,那么我们把这些路径经过 \(y=x+1\) 以后的那段沿着 \(y=x+1\) 对称上去以后,就变成了从 \((0,0)\) 到 \((n-1,n+1)\) 的一段,这显然是 \(\displaystyle \binom {2n} {n+1}\)
两者相减即可
因此我们的最终递推式为 \(Catalan_n=\displaystyle \binom {2n} n - \displaystyle \binom {2n} {n+1}=\dfrac 1 {n+1} \displaystyle \binom {2n} n\)
rancy 引理
对于 \(x_1,x_2\dots x_m\),若 \(\displaystyle \sum _{i=1}^mx_i=1\),则必定存在一种圆排或者说循环位移使得恰好有一个满足前缀和都是正数

我们首先绘成前缀和折线统计图,大概是长成这个模样的
然后我们找到最低点,如果有多个就去找最右侧的

我们很容易发现,对于这个来说,从点 \(low\) 到最后一个点的前缀和 \(\mid 1-val_{low}\mid\)
中间的几段可以抵消掉,最后还会剩下最后一段上升的和最开始的一段上升的,合起来就是 \(\mid 1-val_{low}\mid\)
那么从 \(0\) 号点开始的那个点最坏情况下就是直接往下,此时最多减少 \(val_{low}\) 显然前面的比 \(val_{low}\) 要大,原因是 \(val_{low}\) 的值恒 \(\le 0\),后面的一堆就是起起伏伏但是一段的和都为0,且由于刚才我们的那一段已经到了最低点,所以后面的都是先上升一段后下降一段,必然不会造成影响,因此我们就证明了必然存在一个点使得前缀和不大于 \(0\)
那么怎么证明唯一性呢?
首先如果我们的 \(low\) 点以后的和为 \(\mid 1-val_{low}\mid\),这个值是 \(\ge 1\) 的,所以 \(low\) 点之前的点的和必然 \(\le 0\),这些点必然不合法
同时我们的 \(low\) 点后面的那个点必然是上升,所以说这条线段的增加量 \(\ge 1\),因此如果你选择 \(low\) 后面的点的话,你在最后才能加上这一段,那你在到达 \(low\) 点的时候,你的线段和至多为 \(-val_{low}\),加上 \(val_{low}\) 后必然 \(\le0\)
因此我们通过反证法证明了存在且唯一存在
容斥原理
首先我们考虑比较简单的一些操作
如果班里面语文好的有 15 人,数学好的有 25 人,英语好的有 20人,那么请问至少喜欢一门的有多少人?
答案很显然不能是直接相加,因为会有重复的
此时我们引入容斥原理
化简后得到
但是证明很容易,我们考虑单独拎出来一个元素,假设它出现在集合 \(T_1,T2\dots T_n\) 计算其出现的次数,那么它们这些集合正好就是一些个单个贡献,两两贡献等等,最后就是我们下面的这些东西了
显然后面的这个是二项式定理,直接求解就有 \(1-0=1\)
对于全集 U 下的 集合的并 可以使用容斥原理计算,而集合的交则用全集减去 补集的并集 求得:
容斥定理一般化
容斥原理常用于集合的计数问题,而对于两个集合的函数 \(f(S),g(S)\),若
则
证明太难了,可以看这,自己也写一下,不过不需要掌握
后半部分求和与Q无关,先不考虑
记关于集合 \(P\) 的函数 \(F(P)=\sum_{T\subseteq P}(-1)^{|P|-|T|}\),并化简这个函数:
因此原来的式子的值是
发现仅当 \(\displaystyle |S\setminus Q|=0\) 时有 \(0^0=1\),此时 \(Q=S\),对答案的贡献恰好为 \(g(S)\),其他时候都为0,于是有
推论:
则
理论来说这个推论是补集形式,和上面差不多
斯特林数
第二类斯特林数:可以记作:\(S(n,k)\),或 \(\begin{Bmatrix} n\\k\end{Bmatrix}\)(吐槽一句太难写了吧)
表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个互不区分的非空子集的方案数。
递推式:
边界是 \(\begin{Bmatrix} n\\k\end{Bmatrix}=[n=0]\)
组合意义的证明就是:
单独放进一个新的子集,有 \(\begin{Bmatrix} n-1\\k-1\end{Bmatrix}\) 种方案
放入一个已经有的子集里面有 \(k\begin{Bmatrix} n-1\\k\end{Bmatrix}\) 种方案,两者加起来就行
通项公式:
使用容斥原理证明该公式。设将 \(n\) 个两两不同的元素,划分到 \(k\) 个两两不同的集合(允许空集)的方案数为 \(G_k\),将 \(n\) 个两两不同的元素,划分到 \(k\) 个两两不同的非空集合(不允许空集)的方案数为 \(F_k\)。
于是我们有:
\(\displaystyle G_k=k^n\)
\(\displaystyle G_k=\sum_{j=0}^k\binom {k} {j} F_j\)
第一个式子的话,每一个数都有 \(k\) 个位置可以选,所以即为 \(k^n\)
第二个式子的话,我们可以理解成先空出来 \(j\) 个位置,此时的答案是 \(\displaystyle \binom k jF(j)\),我们把空出来的整到一块就是这个式子了
二项式反演式子如下:
证明网上看看得了,不会想证
因此我们可以用二项式定理去化简上面的那个东西(警告:开始大力推式子)
考虑 \(F_i\) 和 \(\begin{Bmatrix} {n}\\{i}\end{Bmatrix}\) 的关系,相当于这一堆集合,我们可以任意变换位置,那么就和组合数和排列数的区别一样了,因此 \(F_i\) 应该是
\(\displaystyle \begin{Bmatrix} {n}\\{i}\end{Bmatrix}\) 的 \(i!\) 倍,因此
二项式反演
形式1:
证明:
然后右边乘上一个 \(1^{n-j-t}\) 就是一个二项式定,只有 \(j=n\) 的时候右侧的求和为 1,其余的时候都是 0
两边恒成立,得证
形式2:
证明:
更改一个我疑惑了很长时间的误区:
建议先看后面再回来看这个
后面我们将会说至多和至少的概念,这里和我们传统理解的是不一样的,这里的至多至少的方案数内部是有被重复计算的,这里之所以会重复是因为至少和至多的方案数是由钦定产生的。
至多是钦定 \(i\) 个不受限制选。
至少是钦定 \(i\) 个受限制选。
举个例子,假如说一个人有 \(n\) 样物品,问你从中至少选 \(k\) 样的方案数,假设 \(f(i)\) 这里表示至少选 \(i\) 种物品的方案数,那么 \(f(i)\) 就应该是先钦定选了 \(i\) 个,然后剩下的都是可选可不选,这么算出来的,列出式子应该是 \(\displaystyle \binom n i 2^{n-i}\)。实际上很容易发现,这样算是有重复计算的部分,假设 \(g(i)\) 表示恰好选 \(i\) 种的方案数,我们想用 \(g(i)\) 来表示 \(f(i)\),就不能只是单纯的 \(\displaystyle \sum_{j=i}^n g(j)\) 后缀和了,容易发现,\(f(i)\) 应该是由 \(\displaystyle\sum_{j=i}^n \binom j i g(j)\) 得到,这里的系数可以想作是在这 \(j\) 个元素里面钦定的是哪几个,后面的至多是同理的,不过是钦定和非钦定的表现
二项式反演有几个很重要的套路
恰好和至多的转换
设 \(f_i\) 表示恰好时的方案数,\(g_i\) 表示至多时的方案数,易得
由形式1可以反演
这样就可以从至多的方案数推出恰好的方案数
恰好和至少的转换
设 \(f_i\) 表示恰好 \(i\) 个满足某种条件时的方案数,\(g_i\) 表示钦定 \(i\) 个满足某种条件时的方案数,易得
由形式2可以反演

