KMP
KMP算法
前提介绍
KMP算法是一种看模式串在主串中出现次数的优化算法 复杂度为O(n+m)
这个算法理解了不难,不理解只背模板早晚会挂,而且容易忘,建议从头到尾一步一步看完
为了方便描述,我们把S作为子串,T作为模式串,然后下标一定要从1开
设len1为长串,len2为模式串(即短串)
本讲解是参考李煜东蓝书的,把部分不易懂的写了出来,希望对大家有帮助
next数组求解
短串: A B A B A A
下标: 1 2 3 4 5 6
数组: 0 0 1 2 3 1
数组指nxt数组
nxt[2]代表s[1]~s[2]即"AB",前缀为"A",后缀为“B",共有元素的长度为0.
nxt[3]代表s[1]~s[3]即"ABA",前缀为"AB",后缀为"BA",最大前后缀即"A",长度为1.
nxt[4]代表s[1]-s[4]即"ABAB",前缀为"ABA"后缀为“BAB",最大前后缀即"AB",长度为2.
nxt[5]代表s[1]~s[5]即"ABABA",前缀为"ABAB",后缀为"BABA",最大前后缀即"ABA",长度为3.
nxt[i] 表示从第1位到第i位 除去前后都是自身的最大前后缀(所以上面的例子不能有nxt[6])
我们先好好理解一下nxt数组的意思,然后大声喊十遍:nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,nxt是最大前后缀,
相信大家都已经喊完了,或者跳过了,然后我们看如何求解nxt数组:
朴素做法
对于 \(A[1 - i]\)依次枚举 \(j∈[1,i-1]\), 并检查 \(A[i-j+1,i]\) 和 \(A[1,j]\),复杂度\(O((len2)^3)\)
然后我尝试着写了份代码(最好还是看一看挺好懂的):
for(int i=1;i<=len2;i++){
for(int j=i-1;j;j--){
int flag=0;
int k=i-j;//k是用来检验后串
for(int n=1;n<=j;n++){
if(t[n]!=t[k+n]){
flag=1;
break;
}
}
if(!flag){
nxt[i]=max(nxt[i],j);
break;
}
}
}
KMP优化
在讲KMP思想之前
我们先证明几个有关KMP的引理
引理
我们先引入一个概念:候选项
如果存在一个j使得\(A[1,j]\)和\(A[i-j+1,i]\)相等,那么我们就能认为\(j\)是\(nxt[i]\)的一个候选项,很显然,\(1 \le j \le nxt[i]\)
现在我们需要证明:若\(j_0\)是\(nxt[i]\)的一个候选项,则小于\(j_0\)的最大的\(nxt[i]\)的候选项是\(nxt[j_0]\)。换言之,\([nxt[j_0]+1,j_0-1]\)之间一定不含\(nxt[i]\)的候选项
这个玩意很重要,看出来这个你的kmp就学完了
这个要用反证法:
假设在\([nxt[j_0]+1,j_0-1]\)之间存在一个\(j_1\)可以当作候选项
我们可以发现,若\(j_1\)是候选项我们可以列出下面两个式子
\(A[1,j_1]\) = \(A[i-j_1+1,i]\)
\(A[1,j_0]\) = \(A[i-j_0+1,i]\)
然后由于是前后缀,所以说第二个式子的每边的后k个也是相等的
\(A[j_0-k+1,j_0]\) = \(A[i-k+1,i]\)
我们钦定\(k=j_1\)
所以说
\(A[j_0-j_1+1,j_0]\) = \(A[i-j_1+1,i]\)
发现和第一个式子有重合,直接把第二个式子换成
\(A[1,j_1]\) = \(A[j_0-j_1+1,j_0]\)
与\(nxt[j_0]\)的最大的性质不符,故假设不成立,即引理正确
如果看不懂,不用看上面的一堆式子直接看图就明白了!
设最浅的块是a,其次是b,最深的是c
则:\(c\)为\(nxt[j_0]\)
\(b+c\) 为 \(j_1\)
\(a+b+c\) 是 \(j_0\)
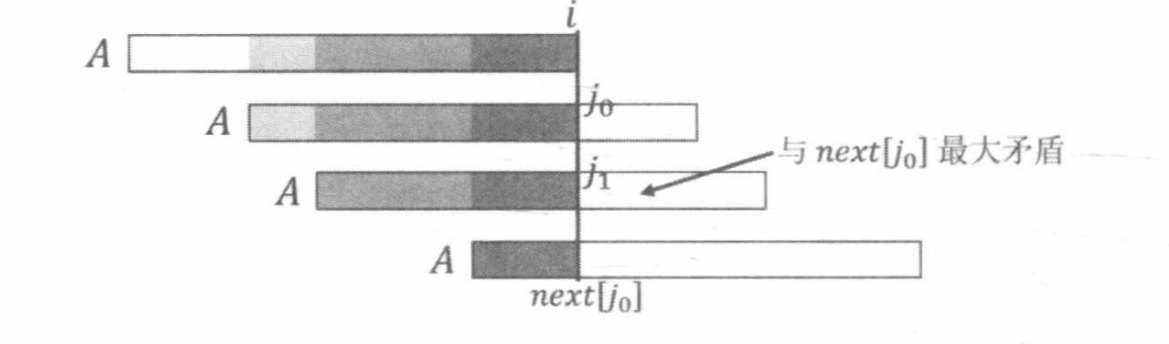
KMP的操作及实现
由刚才我们发现的这一性质,我们可以发现KMP的若干性质
1.我们可以发现当\(nxt[i-1]\)确认时,我们就可以知道\(nxt[i]\)的所有border从大到小是\(nxt[nxt[i]]\),\(nxt[nxt[nxt[i]]]\)……
2.我们还可以发现若\(j\)是\(nxt[i]\)的border,那么\(j-1\)也是\(nxt[i-1]\)的border
证明
这个证明很显然,\(j\)如果说是\(nxt[i]\)的border,则\(A[i-j+1,i]\)和\(A[1,j]\)相等
所以说\(A[i-j+1,i-1]\)和\(A[1,j-1]\)必然相等
所以我们在计算\(nxt[i]\)时,只需要把\(nxt[i-1]+1\) , \(nxt[nxt[i-1]]+1\) , \(nxt[nxt[nxt[i-1]]]+1\) ……
作为border即可,且它们一定是从大到小排列
最后,我们就可以告诉大家怎么求了
首先,我们把\(nxt[1]\)赋为0
假设我们已经处理到第\(i\)位(\(2\leq i\leq len\))
那么此时\(nxt[1]\)到\(nxt[i]\)的值都是已知的
我们假设当前的候选项是\(j\)
我们要处理\(i+1\)时,若\(j+1\)和\(i+1\)不可以匹配就让\(j\)跳到\(nxt[i]\),若可以匹配或者现在border已经变成0了,就要把\(nxt[i+1]\)搞成\(j\)
放个代码
const int N=1e6+10;
int nxt[N];char s[N],t[N];
int n,m,f[N];//s是短串,t是长串
void get_nxt(){
for(int i=2,j=0;i<=n;i++){
while(s[j+1]!=s[i] && j) j=nxt[j];
if(s[j+1]==s[i]) j++;
nxt[i]=j;
}
}
然后有人要问了,那你求\(nxt\)有什么意义吗,我们要求的不是\(nxt\)啊
那么我们此时再假设一个\(f\)数组表示\(f[i]=max\){\(j\)},\(j\)表示S的前j位与T的\(T[i-j+1,i]\)位相等
我们发现是不是\(f\)数组的定义其实和\(T\)数组几乎一样啊
所以我们可以直接用求\(nxt\)数组的思想,写出求长串的思想:
void get_f(){
for(int i=1,j=0;i<=m;i++){
while(j && (s[j+1]!=t[i] || j==n)) j=nxt[j];
if(s[j+1]==t[i]) j++;
f[i]=j
if(f[i]==n) cout<<i-n+1<<endl;//如果S串整个串都出现了,就输出匹配的第一个位置
}
}


