哈希表基础

哈希算法基础

字符串哈希本质上来说就是把每个不同的子串换成一个整数，然后查询两个字符串是否相同时只需要查明两个字符串的哈希值是否相等就行

hash公式

const int base=10;
const int p1=1610612741;
const int p2=805306457;
char s[N];
void hash1(int len){
    for(int i=1;i<=len;i++){
        int p=s[i]-'a';
        hash1[i]=(hash1[i-1]*base+p)%p1;
        pw1[i]=pw1[i-1]*base%p1;
    }
}
void hash2(int len){
    for(int i=1;i<=len;i++){
        int p=s[i]-'a';
        hash2[i]=(hash2[i-1]*base+p)%p2;
        pw2[i]=pw2[i-1]*base%p2;
    }
}

为什么要用两次哈希呢？我们发现，hash的值很容易冲突，可能两个数字%同一个数的结果也相同
所以，我们应该用双哈希甚至三哈希，并用一些不常见的模数（温馨提示：现在1e9+7，998244353等数极易被卡）

但是如果是查询一段区间的中间的某一个子串怎么办呢……
这时候就要用到上面的一个pw数组了

$ hash=((hash[r]−hash[l−1]∗pw[{r-l+1}])%mod+mod)%mod$

（这个很显然吧）

证明如下：

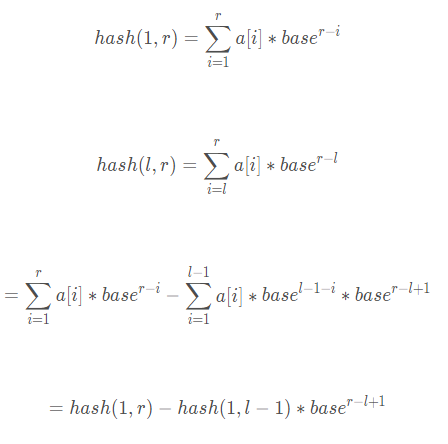
说简单点，这就是一个进制的问题

那么我们的子串也就可以自然而然的写出来了

long long get_hash1(int l,int r){
    return (((hash1[r]-hash1[l-l]*pw1[r-l+1])%p1)+p1)%p1;
}
//另一个咕了

剩下的操作下次再写