图的存边

在图论中，最基本的应该就是建边了

1.邻接矩阵

最简单，最直接的办法，就是整一个二维数组 f[10000][10000]
f[i][j]=w 表示从i点到j点有一条权值为w的边，如果没有权值，可以赋值为1,0来区别是否油边
代码大概长成这样：

const int N=1e4+10;
int f[N][N];
void add(int u,int v,int w){
	f[u][v]=w;
}
int main(){
    int m;
    scanf("%d",&m);
    while(m--){
        int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        void(x,y,w);
    }
}

优势：稠密图中表现仍然良好
劣势：二维数组能开的数量有限，对于m>1e4的数据束手无策

2.邻接表：

上面的图的问题在于空间的问题，那我们就借此观察如何优化
我们发现，上面的二维数组我们可以转化成链表，用链表存图

此时我们可以用结构体来存边

struct edge{
    int to,nxt,w;
}e[N];
int head[N];

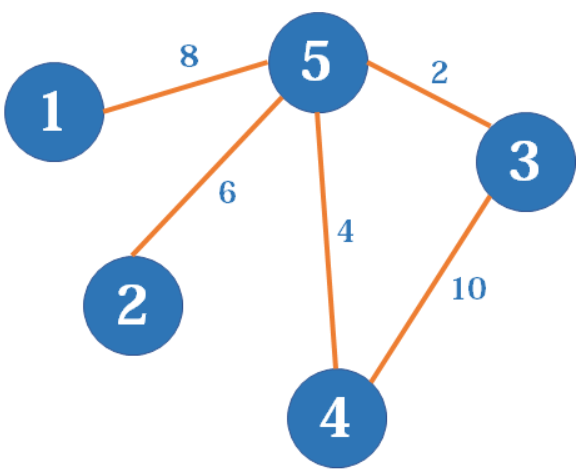
就说这个图吧，我们思考如何用链表实现边与边的连通
为了懒方便，我们用vector来存邻接表
核心思想的话就是存储每个顶点能够到达哪些顶点。

vector<edge> e[MAXN];
inline void add(int from, int to, int w){
    edge e={to, w};
    edges[from].push_back(e);  //向vector的最后添加一条边
}
遍历图时用通常遍历数组的方法即可

但是考虑到vector常数大的问题，我们此时还是直接用数组

int cnt=0;
void add(int u,int v,int w){//边的起始点，终点，权值
	e[++cnt].to=v;
	e[cnt].val=w;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}

如果想遍历这个点和哪些能到达的距离为1的点的话

for(int i=head[u];i;i=e[i].nxt){
	/*此时的e[i].to指的是点u的下一个节点的id，e[i].val指的是到v的长度*/
}

3.链式前向星(一般都用这个)

这种做法是用数组模拟链表
As we all know:STL’s 常数 is very 的大
所以这个存图方式算是比上一个又优化了不少（其实可以数组模拟链表，但是据某位@Locura大佬所说：“正经人谁写链表啊！！！”）
核心代码如下：

#include<iostream>
using namespace std;
const int N=1e5+10;
int n,cnt;
struct node{
    int w,to,nxt;
}e[N];
int head[N];
void add(int u,int v,int w){
    e[++cnt].to=v;
    e[cnt].w=w;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
int main(){
    scanf("%d",&n);//添加几条边
    while(n--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);//添加一条以a为起点，b为终点，权值为c的边
    }
    cout<<endl;
    for(int start=1;start<=6;start++){
        for(int i=head[start];i;i=e[i].nxt) cout<<start<<" "<<e[i].to<<" "<<e[i].w<<endl;
    }
    return 0;   
}
/*
5
1 3 5
2 4 5
4 3 6
6 1 4
1 4 3
*/