问题的抛出:
版权声明:本文为博主原创文章,转载请附上原文出处链接和本声明。2019-10-03,00:56:39。
作者By-----溺心与沉浮----博客园
为什么两个浮点数相减时,有时出乎我们意料之外的值呢?例如3.1415927 - 3.1415926 = 0.0000002?(例子我随便举得,大家不要在乎这个,例子中这个值我也没有碰到过,但我相信大家在做浮点数运算时,肯定有这种类似的情况)这涉及到精确问题。
1/3用分数可以来很好的表示,可是如果不允许用分数表示呢?如何保证数尽可能的等于1/3呢?相信大家都知道,0.3......小数点后面3的数量越多,表示的就更加靠近。
就如十进制系统中不能准确表示出1/3!同样二进制系统也无法准确表示1/10。这也就解释了为什么浮点型减法出现了“减不尽”的精度丢失问题。
概述:
float和double在存储方式上都是遵从IEEE的规范的,float的存储方式如下图所示:

double的存储方式如下图所示:

步骤:
将一个float型转化为内存存储格式的步骤为:
1、先将这个实数的绝对值化为二进制格式
2、将这个二进制格式实数的小数点左移或右移n位,直到小数点移动到第一个有效数字的右边。(请类比十进制的科学计数法)
3、从小数点右边第一位开始数出二十三位数字放入第22到第0位。
4、如果实数是正的,则在第31位放入“0”,否则放入“1”。
5、如果n 是左移得到的,说明指数是正的,第30位放入“1”。如果n是右移得到的或n=0,则第30位放入“0”。
6、如果n是左移得到的,则将n减去1后化为二进制,并在左边加“0”补足七位,放入第29到第23位。 如果n是右移得到的或n=0,则将n化为二进制后在左边加“0”补足七位,再各位求反,再放入第29到第23位。
首先我们需要搞清楚下面两个问题:
(1)十进制整数如何转化为二进制数
算法很简单,举个例子,11表示成二进制数:
11 / 2 余 1
5 / 2 余 1
2 / 2 余 0
1 / 2 余 1
0结束 11进制表示为(从下往上)1011
这里提一点,只要遇到除以后的结果为0了就结束了,大家想想,所有的整数除以2是不是一定能够最终得到0呢。换句话说,所有的整数转变为二进制数的算法会不会无线循环下去呢?绝对不会,整数永远可以用二进制精确表示,但小数不一定了。
(2)十进制小数如何转化为二进制数
算法是乘以2直到没有了小数为止。举个例子,0.9表示成二进制数
0.9 × 2 = 1.8 取整数部分 1
0.8(1.8的小数部分) × 2 = 1.6 取整数部分 1
0.6 × 2 = 1.2 取整数部分 1
0.2 × 2 = 0.4 取整数部分 0
0.4 × 2 = 0.8 取整数部分 0
0.8 × 2 = 1.6 取整数部分 1
0.6 × 2 = 1.2 取整数部分 1
0.2 × 2 = 0.4 取整数部分 0
0.4 × 2 = 0.8 取整数部分 0
...... 0.9二进制表示为(从上往下):11100110011001100......
注意:上面的计算过程循环了,相信你也发现了,也就是说本例子中0.9×2永远不可能消灭小数部分,这样算法讲无限循环下去。很显然,小数的二进制表示有时是不可能精确的。其实道理很简单,十进制系统中能不能准确表示处1/3呢?同样二进制系统也无法准确表示1/10。这也就解释了为什么浮点型减法出现了“减不尽”的精度丢失问题。
举例:
以8.25举例,看看8.23在计算中是如何存储的
(1)首先将整数部分8转换成2进制
8 / 2 余 0
4 / 2 余 0
2 / 2 余 0
1 / 2 余 1

(2)小数部分0.25转换成二进制
0.25 × 2 = 0.5 取整数部分 0
0.5 × 2 = 1.0 取整数部分 1

(3)整数部分与小数部分都已转换成了二进制,那么8.25的二进制表示为1000.01,虽然是可以这么表示了,但是计算机认识吗?所有的内容(数,字母,汉字,符号)在计算机世界里只有2种形态,0和1,因此这不是我们最终要展现的数!
(4)8.25---->>>1000.01用二进制的科学计数法表示(还记得十进制的科学计数法吗?换个进制来使用)1.00001 × 2的3次方,指数为3。
(5)首先8.25我们表现形式是正数,那么31位中填0(记得前面说的有符号数与无符号数的博文吗?),0x7FFFFFFF, 0x80000000这两个数便是有符号数的一个界限,所以在有符号数中最高位为1,代表负,最高位为0,代表正!
但0x80000000它一定代表着负数吗?不是,在无符号数中,最高位为1,依然是正数。怎么区分,看使用者如何定义。这里我不做介绍了!
正数,符号位,我们在第31位中填0,
指数部分,我们的n是左移得到的,说明我们的指数为正,因此第30位我们填1,然后我们将指数n减1,得到2,它的二进制是10,并在左边添0,从第29位开始到第23位,我们凑够7位,因此指数部分是10000010

(6)22 - 0尾数部分怎么填呢?我们8.25转换成二进制不是1000.01也即1.00001 × 2的3次方吗?我们取科学计数法小数点后面的数,从第22位开始,全部往里扔,后面不足全部补0

(7)最终的表示:

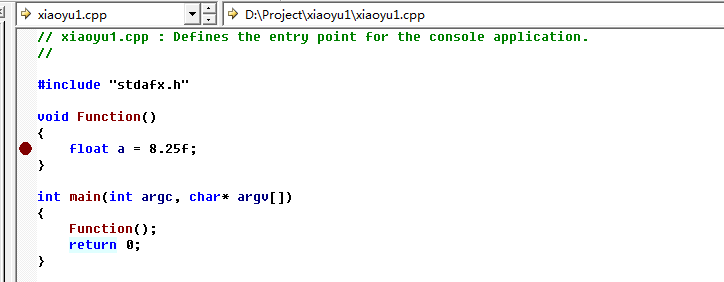
整理一下,我们得到:0100 0001 0000 0100 0000 0000 0000 0000,这便是我们最终需要的二进制表示形式,转换成16进制为:0x41040000,我们用编译器查看一下
1 // xiaoyu1.cpp : Defines the entry point for the console application.
2 //
3
4 #include "stdafx.h"
5
6 void Function()
7 {
8 float a = 8.25f;
9 }
10
11 int main(int argc, char* argv[])
12 {
13 Function();
14 return 0;
15 }
1 6: void Function()
2 7: {
3 00401020 push ebp
4 00401021 mov ebp,esp
5 00401023 sub esp,44h
6 00401026 push ebx
7 00401027 push esi
8 00401028 push edi
9 00401029 lea edi,[ebp-44h]
10 0040102C mov ecx,11h
11 00401031 mov eax,0CCCCCCCCh
12 00401036 rep stos dword ptr [edi]
13 8: float a = 8.25f;
14 00401038 mov dword ptr [ebp-4],41040000h
15 9: }
16 0040103F pop edi
17 00401040 pop esi
18 00401041 pop ebx
19 00401042 mov esp,ebp
20 00401044 pop ebp
21 00401045 ret

通过反汇编查看得知,压入栈中的8.25,是0x41040000
例子2
既然8.25的会了,那么-8.25呢?如何表示呢?
很简单,首先将-8.25的绝对值用二进制表示出来就行了!跟8.25表示形式一模一样,只不过第31位为1,因为是负数,所以-8.25的最终二进制表示为0xC1040000,我们反汇编查看一下。看是不是这个呢?
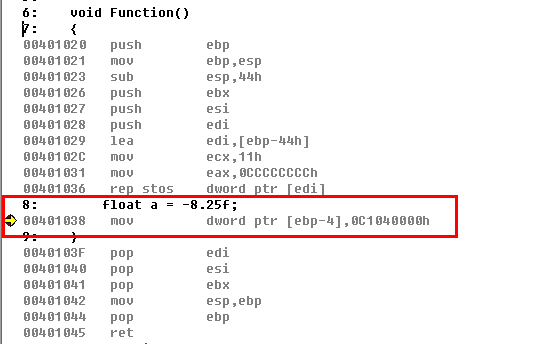
经过反汇编观察,发现与我们计算结果一致吧~~~~~
例子3
如何将一个只有小数部分的数用二进制来表示呢?(这也是一个难点,与有整数部分不一样的是,只有小数部分的数,通常它的科学计数法表示中指数为负),我们还没有探讨过指数为负的情况!
我以0.25为例!
0.25的二进制表示为:
0.25 × 2 = 0.5 取整数部分为 0
0.5 × 2 = 0.5 取整数部分为 1

(1)0.25用二进制表示为0.01,用科学计数法来表示为1 × 2的负2次方,0.25为正数,因此第31为为0,指数n向右得到,因此第30为为0,指数n(-2)减1得到-3,-3用32位来表示是0xFFFFFFFD,FD为1111 1101,从最低位开始数7个数出来放入23到29中

(2)尾数部分,0.01的科学计数法为1.0 × 2的负2次方,小数点后面为0,因此,22 -0位中全部添0即可,最终表示为0011 1110 1000 0000 0000 0000 0000 0000,用十六进制表示为0x3E800000,我们反汇编观察看看

例子4
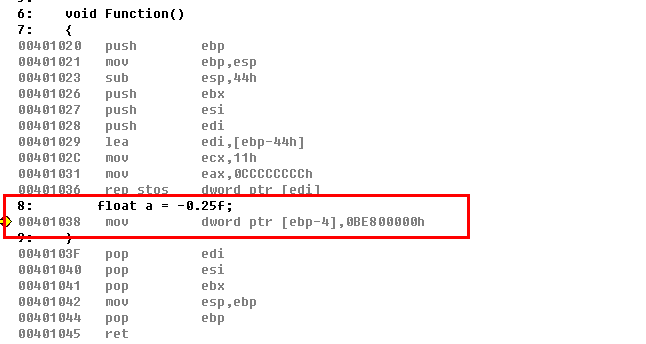
-0.25呢?如何表示呢?
0xBE800000,读者自己去试试吧,其实也不用试,十分简单,我刚才不是算了0.25的了吗?只需要把0.25的二进制表示复制过来,然后第31位改成1就是-0.25的值了~~~~
float与double
float在内存中占4字节,double在内存中占8个字节,如果读者您弄懂了上面的过程的话,相信你也一定明白了double的存储过程,double存储中提供了更多的尾数部分,这为小数点后面的精确度提供了更多的位数!使值更加精确,就像是99.99%与99.9999999999999999999999999999999999%的区别,就像是买黄金,如果只是商品交易,那么99.99%那么完全够用了,因为99.99%它就可以说成是24K纯金,但是科学实验中呢?99.99%纯吗?它肯定没有99.9999999999999999999999999999999999%纯度高对吧!因为后者表示的精度更高,在平时中的程序中,float代表的精度其实已经足够我们使用,因此,在平时代码编写中,float定义小数就足够了,及其特殊情况下我们采用double,明白了小数在计算机中是如何存数的了吗?



