由于写EFLAGE博文中,有关C位,P位,O位,我觉得我没有描述清楚,而且C位也没有演示过借位情况,P位中也有些坑没讲,我还是决定再补一篇,争取把每个标志位描述清楚,不光是让看我文章的人能看的明白,也是自己对知识的巩固加深,虽然没什么技术性的东西,但我一直觉得,再牛的花招它都是由基础构建而出的,相信经过1年,2年,甚至5,6年的积累,也能极大丰富我的知识视野,尽管不一定会记得,但是好记性不如烂笔头,当我遗忘再次不会时,翻开博文一查,肯定会有一种豁然开朗的感觉,那时,我肯定会感激现在的我。千里之行,始于足下。
版权声明:本文为博主原创文章,转载请附上原文出处链接和本声明。2019-08-30,00:40:11。
作者By-----溺心与沉浮----博客园
进位标志CF(Carry Flag):如果运算结果的最高位产生了一个进位或借位,那么,其值为1,否则其值为0。
CF:什么是最高位进位,什么是最高位借位?--------不做术语解释,麻烦,直接看例子,懂了就是懂了,不懂就是把术语记住也没用!
拿例子来讲:我们以0x80 - 0x40举例,一切源于例子,不看术语(以8位为例啊!32位的例子举起来要人命)
1 1000 0000 //0x80对应的二进制
2 0100 0000 //0x70对应的二进制
3 -----------------------
从右往左看,我们按正常人逻辑来从右往左数第7位(按编程人员角度,这是第6位,一般喊第1位喊第0位),0 - 1,不够减,向前一位借,前一位是哪一位,从右到左数,第8位,那这个是不是从最高位借1了呢?我们实验说话!
由于我们是做实验,为了方便观察,老规矩,把EFLAGE所有标志位置0
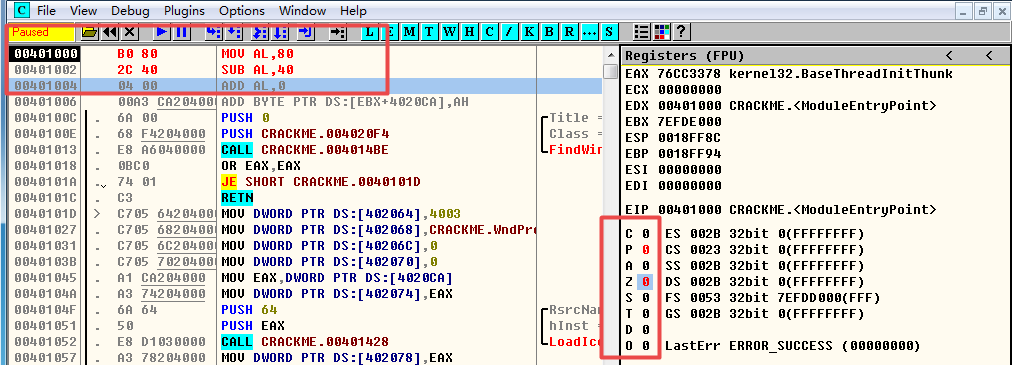
执行代码,只观察C位!
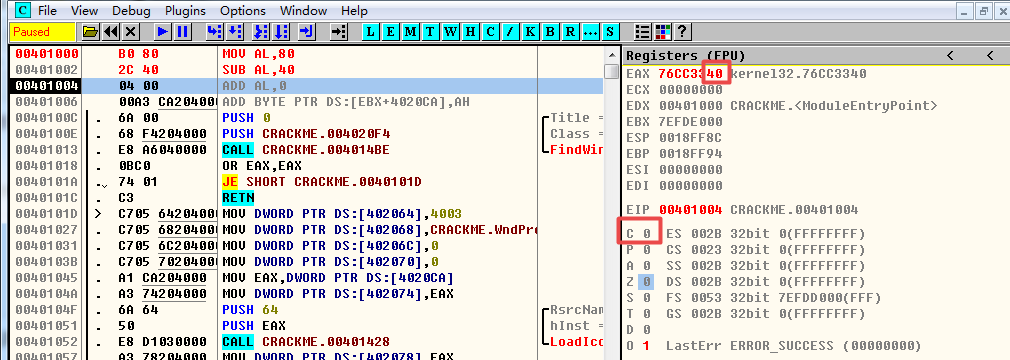
经观察,相减结果为0x40,C位仍然为0,显然,从数据宽度来讲(例子中是以8位为例!!!)我们从最高位第8位借了一个1,但是C位没有变为1,我们对CF的解释是什么?是如果运算结果的最高位产生了一个进位或借位,那么,其值为1,否则其值为0。
既然C位没有发生变化,那么第8位不是我们的最高位,最高位那就是第8位往前的那一个位(请默认计算机只有8位宽度!我们例子讲的是8位!如果要纠结16位,32位,64位,请自行测试举例,当然8位懂了,以此类推,后面的16位,32位,64位也就明白了),显然前面那个位不存在,不存在难道就不减了吗?不,要减,只不过需要我们从一个不存在的位数借一个数去减
那么加法呢,加法导致运算结果超出了怎么办?好办,超出的位全部抛弃掉,不要了,我存不了!就像水杯,水装满了怎么办,那怎么办,水它自己溢出了呀!
我们再举一例子,C位因借位而置1的情况
1 MOV AL,80
2 SUB AL,81
1 1000 0000 //0x80对应的二进制
2 1000 0001 //0x81对应的二进制
3 -----------------------------
我们自己推一下,右数第一位不够减,向高位借一个1,中间的高位都是0,借不了,那就一直往前借,然后减完,前面7位结果肯定是111 11111,第8位给借走了,它自己也变成0了,自己不够减了怎么办,没办法,它也得向不存在的高位去借一个1来,(这是啥啊,这是二进制啊!!!高位的1相当于低下一位的2呀,但是2进制没有2啊,十进制也没有十是一样的)于是减完的结果就变成了1111 1111,我们实验一下,观察结果。

实验结果符合我们的预期,说明我们的猜测是正确的!通过实验,相信什么是最高位应该能明白了吧!
奇偶标志PF(Parity Flag):奇偶标志PF用于反映运算结果中“1”的个数的奇偶性。
如果“1”的个数为偶数,则PF的值为1,否则其值为0。
如果你亲自动手通过代码,仅改变EFLAG中PF一个标志位的话,相信你跟我一样碰到过一种情况,那就是明明我运算结果是偶数个1啊,为什么PF位还是0呢?根据官方解释,奇偶标志PF用于反映运算结果中“1”的个数的奇偶性。如果“1”的个数为偶数,则PF的值为1,否则其值为0。没错呀,是这样啊,那为什么明明运算结果是偶数个1,为什么还是0呢?
我们看看实例
1 MOV AX,0xB03
2 ADD AX,0x1
我们自己验证一遍,0xB03加上0x1,运算结果是0xB04,对应的二进制是0000 1011 0000 0100,运算结果是4个1,从上面定义来讲,P位是1,试验验证一次。

验证发现我们根据定义推论的结果错误,那么我们在上面代码的基础上再加一个1试试看,那么运算结果是0xB05是吧!对应的二进制是0000 1011 0000 0101,数一数,一共是5个1,根据定义,PF位是0是吧,我们实验验证一次。

又发现我们根据定义推论的结果错误,计算结果偶数个1居然为0,奇数个1居然为1,这不与定义相反吗?这并不相反,PF位实际只是最低字节有效!!!!也就是说,不管你是8位,16位,32位也好(64位我没环境,没测),它只看你最低有效字节(8个位),最低有效字节是偶数个1,那么PF就是1,最低有效字节是奇数个1,那么PF就是0。
与定义相同的测试结果请看博主写的EFALG那篇博文
版权声明:本文为博主原创文章,转载请附上原文出处链接和本声明。2019-08-30,00:40:11。
作者By-----溺心与沉浮----博客园
溢出标志OF(Overflow Flag):溢出标志OF用于反映有符号数加减运算所得结果是否溢出。
如果运算结果超过当前运算位数所能表示的范围,则称为溢出,OF的值被置为1,否则,OF的值被清为0。
先来说说,计算机是如何判断有溢出的,比如0x80 - 0x40
1 MOV AL,0x80
2 SUB AL,0x40
这里需要说明一点,计算机它只会做加法
因此我们可以等同看待下面的代码
1 MOV AL,0x80
2 ADD AL,-40 //OD它会自动将这行代码转换成ADD AL,0xC0
因此也等同于下面这段代码,其实也就是这段
MOV AL,0x80
ADD AL,0xC0
1000 0000
1100 0000
-------------------
0100 0000
我们前面说过,计算机不管正数与负数,这个取决于使用者怎么定义(char, unsigned char),
(介绍两个概念,本想着全靠实验全部都已白话文形式描述的,结果还是不得不介绍术语了,汗)
符号位
我们这里把它当做有符号位看待,最高位就是符号位
最高有效数值位:紧挨着最高位的旁边那个位,从右往左数,也即第7位
如果符号位有进位,1,没有就是0(什么是符号位有进位?如果最高位相加,往前进位了,之前我们称溢出(针对无符号数),现在我们称有发生进位)
最高有效数值位向符号位产生进位,1,没有就是0。
然后计算机会拿这两个数进行异或(XOR),如果异或结果为1,OF位就为1,如果异或结果为0,OF位就为0
如果前面中的EFLAG博文,O位,C位发生进位的那几种情况有弄明白的话,其实这里都是多余的,尽管笔者自己自己也有时候犯懵,也不是说不懂这个,只是这一块的反应会慢一点,但多次举例,反复练习,写笔记,也比刚开始顺溜许多了,或许有一天我还是会懵圈,遗忘,但是我把自己踩过的坑一点不落的写了下来,日后回头看,也会避免将来再去踩坑,希望这些也能够帮助后来者学习。其实文章写到这,我也发现自己写啰嗦了,不过就是有符号,无符号两种情况的溢出与不溢出,但写清楚就是为了能更好的去理解本质,带来的问题就是过于啰嗦,适得其反。但这些的确也是曾经困扰过我的东西,我就是想把这些坑都写一遍,然后在自己脑海中过一遍,熟悉一遍。
最高位进位与溢出的区别:
进位标志表示无符号数运算结果是否超出范围.
溢出标志表示有符号数运算结果是否超出范围.
溢出主要是给有符号运算使用的,在有符号的运算中,有如下的规律:
正 + 正 = 正 如果结果是负数,则说明有溢出
负 + 负 = 负 如果结果是正数,则说明有溢出
正 + 负 永远都不会有溢出.
几种情况-------------------------------------------------
1、无符号、有符号都不溢出
2、无符号溢出、有符号不溢出
3、无符号不溢出、有符号溢出
4、无符号、有符号都溢出
这四种情况在前面EFLAG博文中有介绍举例
------------------------------------------------------------
不知不觉,又要凌晨一点了,就这么点东西,花了2个钟头去整理去复习,也真是够花时间的,呵呵,也没啥,算是对自己成长点点滴滴的记录吧,千里之行,始于足下,这些说对我有用吧,我写这些东西的时间都足够去学很多新知识了,说没用吧,又让我对这些旧知识重新拾了一遍而且有了更深刻的理解。不多说了,睡觉!毕竟还得要上班挣钱把小日子过下去。。。
版权声明:本文为博主原创文章,转载请附上原文出处链接和本声明。2019-08-30,00:40:11。
作者By-----溺心与沉浮----博客园



