| Name | Date | Rank | Solved | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020 Multi-University,Nowcoder Day 5 | 2020.07.25 | 86 / 1145 | 5/11 | Ø | O | Ø | O | O | O | × | Ø | O | × | × |
A.Portal(dp)
题目描述
有一个 \(n\) 个点 \(m\) 条边的带权图,你一开始在 \(1\) 号点,要按顺序完成 \(k\) 个任务,第 \(i\) 个任务是先去\(a[i]\) 再走到 \(b[i]\)。当你走到一个点上的时候,可以在这个点创建一个传送门。当同时存在两个传送门的时候,你可以在传送门之间不耗代价地传送。如果已经存在了两个传送门,想再创建一个,就必须选择之前的一个传送门关掉(关掉这个操作不耗时间,并且是远程操作,不需要走过去)。问完成所有任务的最短总行走距离。
数据范围:\(1\leq n,k\leq 300,1\leq m\leq 40000\)。
分析
用动态规划求解。
\(f(i,u,x,y)\) 表示已经完成了第 \(i\) 个任务,当前人在节点 \(u\),传送门在节点 \(x\) 和 \(y\) 时,行走的最短距离。状态过多,显然会 \(\text{MLE}\) 和 \(\text{TLE}\)。
贪心地思考,一直创建两个传送门是没有必要的:若要从 \(x\) 传送到 \(y\),当前节点为 \(u\),那么必须要从 \(u\) 走到 \(x\) 再传送到 \(y\);不妨只在 \(y\) 创建一个传送门,走到 \(x\) 后再设置传送门;也就是说,我们可以随时在当前节点创建传送门。因此,只需要在状态中记录一个传送门的位置即可。\(f(i,u,p)\) 表示已经完成了第 \(i\) 个任务,当前人在节点 \(u\),传送门在节点 \(p\) 时,行走的最短距离。需要继续精简状态。
不妨将 \(k\) 个任务看作一条路径:\(1\to a_1\to b_1\to\cdots\to a_n\to b_n\)。一共有 \(t=2k+1\) 个节点,\(c_i\) 表示第 \(i\) 个节点,其中 \(1\leqslant i\leqslant t\)。\(f(i,p)\) 表示当前人位于节点 \(c_i\),传送门位于节点 \(p\) 时,行走的最短距离。
可以证明,只需要三种转移,即可覆盖所有状态:① 直接从 \(c_{i-1}\)走到 \(c_i\),不更改传送门位置;② 枚举 \(q\),将传送门的位置更改到 \(q\),从 \(c_{i-1}\) 传送到 \(p\),再从 \(p\) 走到 \(q\),将传送门放在 \(q\),再从 \(q\) 走到 \(c_i\);③ 枚举 \(q\),将传送门的位置更改到 \(q\),从 \(c_{i-1}\) 走到 \(q\),将传送门放在 \(q\),再从 \(q\) 传送到 \(p\),从 \(p\) 走到 \(c_i\)。
代码
/*******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第五场) Problem A
Date: 8/24/2020
Description: Dynamic Programming
*******************************************************************/
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int N=705;
//====================
//f[i][j]表示:
// 当前在c[i],传送门在j时;
// 行走的最小路程。
ll f[N][N];
ll dis[N][N];
int c[N];
int n,m;
int t;
int main(){
int i,j,k;
cin>>n>>m>>k;
memset(f,inf,sizeof(f));
memset(dis,inf,sizeof(dis));
for(i=1;i<=n;i++) dis[i][i]=0;
for(i=1;i<=m;i++){
int u,v;
ll w;
scanf("%d%d%lld",&u,&v,&w);
dis[u][v]=min(dis[u][v],w);
dis[v][u]=min(dis[v][u],w);
}
c[++t]=1;
for(i=1;i<=k;i++){
int a,b;
scanf("%d%d",&a,&b);
c[++t]=a;
c[++t]=b;
}
//Floyed算法求(x,y)之间的最短路
for(k=1;k<=n;k++){
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
dis[i][j]=min(dis[i][k]+dis[k][j],dis[i][j]);
}
}
}
for(i=1;i<=n;i++){
//初始化
//当前在c[1]
//传送门设置在i
f[1][i]=dis[1][i];
}
int p,q;
for(i=2;i<=t;i++){
//当前在c[i-1],要走向c[i]
for(p=1;p<=n;p++){
//当前传送门在p
//不改变传送门位置,直接走到 c[i]
f[i][p]=min(f[i][p],f[i-1][p]+dis[c[i-1]][c[i]]);
for(q=1;q<=n;q++){
//从c[i-1]传送到p,路程0
//从p走到q,路程dis[p][q]
//从q走到a[i],路程dis[q][c[i]]
f[i][q]=min(f[i][q],f[i-1][p]+dis[p][q]+dis[q][c[i]]);
//从c[i-1]走到q,路程dis[c[i-1]][q]
//从q传送到p,路程为0
//从p走到c[i],路程dis[q][c[i]]
f[i][q]=min(f[i][q],f[i-1][p]+dis[c[i-1]][q]+dis[p][c[i]]);
}
}
}
ll ans=inf;
for(i=1;i<=n;i++){
ans=min(f[t][i],ans);
}
cout<<ans<<endl;
return 0;
}
B.Graph(异或最小生成树)
题目描述
给一棵 \(n\) 个节点的树,每条边都有一个权值,每次可以做一个操作:加入一条边或者删除一条边。最终使得所有边的权值和最小。
在加入或删除边的时候要满足以下两个条件:
\(1.\) 图始终保持联通。
\(2.\) 每个环上的边的异或和为 \(0\)。
数据范围:\(2\leq n\leq 10^5,0\leq x,y\leq n-1,0\leq z<2^{30}\)。
分析
可以发现,无论添加边的时间顺序,连接点 \(a\) 和点 \(b\) 的边的权值一定是固定的,值为点 \(a\) 到点 \(b\) 路径上的所有边权的异或值,所以题目可以简化成寻找完全图的最小生成树。
设 \(dist[x]\) 为点 \(0\) 到点 \(x\) 上所有边权的异或值,则在完全图中,连接点 \(a\) 和点 \(b\) 的边的权值为 \(dist[x]\oplus dist[y]\),这样就相当于每个点都有一个点权值 \(dist[i]\),用 \(dfs\) 处理即可。
参考 CF888G 的做法,时间复杂度为 \(O(n\log^2n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int trie[N*30][2],a[N],tot=0;
struct Edge
{
int to;
int dis;
int Next;
}edge[N<<1];
int head[N],num_edge;
void add_edge(int from,int to,int dis)
{
edge[++num_edge].to=to;
edge[num_edge].dis=dis;
edge[num_edge].Next=head[from];
head[from]=num_edge;
}
void insert(int x)
{
int p=0;
for(int i=30;i>=0;i--)
{
int ch=(x>>i)&1;
if(!trie[p][ch])
trie[p][ch]=++tot;
p=trie[p][ch];
}
}
int solve(int root1,int root2,int bit)
{
if(bit<0)
return 0;
int ans1=-1,ans2=-1;
if(trie[root1][0]&&trie[root2][0])
ans1=solve(trie[root1][0],trie[root2][0],bit-1);
if(trie[root1][1]&&trie[root2][1])
ans2=solve(trie[root1][1],trie[root2][1],bit-1);
if(ans1>=0&&ans2>=0)
return min(ans1,ans2);
if(ans1>=0)
return ans1;
if(ans2>=0)
return ans2;
if(trie[root1][0]&&trie[root2][1])
ans1=solve(trie[root1][0],trie[root2][1],bit-1)+(1<<bit);
if(trie[root1][1]&&trie[root2][0])
ans2=solve(trie[root1][1],trie[root2][0],bit-1)+(1<<bit);
if(ans1>=0&&ans2>=0)
return min(ans1,ans2);
if(ans1>=0)
return ans1;
if(ans2>=0)
return ans2;
}
long long ans=0;
void dfs(int start,int bit)
{
if(bit<0)
return ;
if(trie[start][0]&&trie[start][1])
ans=ans+1ll*solve(trie[start][0],trie[start][1],bit-1)+(1<<bit);
if(trie[start][0])
dfs(trie[start][0],bit-1);
if(trie[start][1])
dfs(trie[start][1],bit-1);
}
int dist[N];
void init(int x,int fa)
{
for(int i=head[x];i;i=edge[i].Next)
{
int y=edge[i].to,z=edge[i].dis;
if(y==fa)
continue;
dist[y]=dist[x]^z;
init(y,x);
}
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n-1;i++)
{
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
add_edge(x,y,z);
add_edge(y,x,z);
}
init(0,0);
for(int i=0;i<=n-1;i++)
insert(dist[i]);
dfs(0,30);
cout<<ans<<endl;
return 0;
}
C.Easy(生成函数)
题目描述
已知序列 \(a,b\) 满足 \(\displaystyle\sum_{i=1}^{k}a_i=n,\displaystyle\sum_{i=1}^{k}b_i=m\)(\(a_i,b_i\) 均为 正整数),对于所有满足条件的 \(a,b\) 序列,求 \(\displaystyle\prod_{i=1}^{k}\min(a_i,b_i)\) 的和。
数据范围:\(1\leq T\leq 100,1\leq n,m\leq 10^6,1\leq k\leq \min(n,m)\)。
分析
假设 \(N<M\),构造满足 $\displaystyle\sum_{i=1}{k}a_i=n,\displaystyle\sum_{i=1}b_i=m $ 的生成函数:
显然多项式展开后,\(x^ny^m\) 的系数即为不同序列 $a,b $ 的方案数。
由于每一组 \(a_i,b_i\) 对答案的贡献为 \(\min(a_i,b_i)\),因此构造本题答案的生成函数需在含 \(x,y\) 的项之前乘上 \(\min(a_i,b_i)\),构造生成函数 \(S=\displaystyle\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}\min(i,j)x^iy^j\),答案即为 \(S^k\) 的 $xnym $ 的系数。
求出 \(S\) 的封闭形式:
因此 \(S^k=x^ky^kG^k(x)G^k(y)G^k(xy)\),由于 \(G^k(x)=\displaystyle\sum_{i=0}^{\infty}\dbinom{k+i-1}{i}x^i\),答案为 $xnym $ 的系数,即:
时间复杂度 \(O(T\min(n,m))\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int mod=998244353,N=2e6+10;
long long fac[N+10],inv[N+10];
long long quick_pow(long long a,long long b)
{
long long ans=1;
while(b)
{
if(b&1)
ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
long long C(long long n,long long m)
{
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{
fac[0]=1;
for(int i=1;i<=N;i++)
fac[i]=fac[i-1]*i%mod;
inv[N]=quick_pow(fac[N],mod-2);
for(int i=N;i>=1;i--)
inv[i-1]=inv[i]*i%mod;
int T;
cin>>T;
while(T--)
{
long long n,m,k;
cin>>n>>m>>k;
int minn=min(n,m);
long long ans=0;
for(int i=0;i<=minn-k;i++)
{
ans=(ans+C(k+i-1,i)*C(n-i-1,k-1)%mod*C(m-i-1,k-1)%mod)%mod;
}
cout<<ans<<endl;
}
return 0;
}
D.Drop Voicing(断环成链+LIS)
题目描述
给定一个长为 \(n(2\leq n\leq 500)\) 的排列,有两种操作:
\(1.\) 将倒数第二个数放到开头。
\(2.\) 将第一个数放到最后。
连续的操作 \(1\)(包括 \(1\) 次)称为一段。现在要将排列变成 \(1\) ~ \(n\),要使得段数尽可能少,求最小值。
分析
对于操作 \(\text{Drop-2}\),可以将 \(p_1\) ~ \(p_{n-1}\) 看作一个环,环的长度为 \(n-1\),即进行 \(n-1\) 次操作 \(\text{Drop-2}\),排列还原;对于操作 \(\text{Invert}\),可以将 \(p_1\) ~ \(p_n\) 看作一个环,环的长度为 \(n\),即进行 \(n\) 次操作 \(\text{Invert}\),排列还原。形成的两个环如图所示,$\color{red}\surd $ 代表当前排列 \(p\) 的第一个数,\(\color{red}\times\) 代表位于大环(长度为 \(n\) 的环)上,而在小环(长度为 \(n-1\) 的环)外的数。
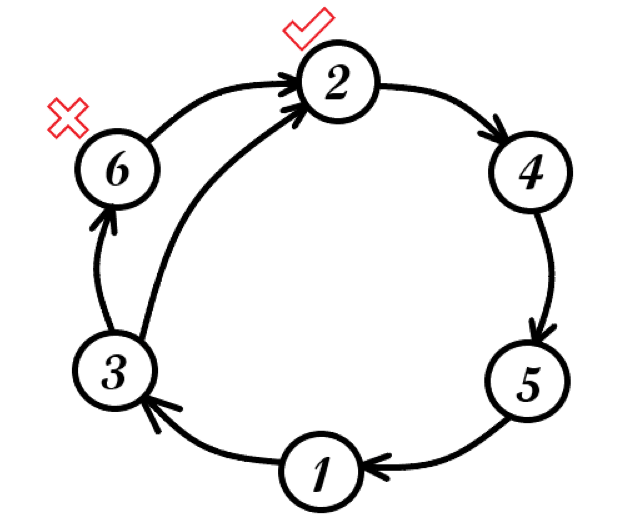
代码
/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第五场) Problem D
Date: 8/20/2020
Description: Circle, LIS
*******************************************************************/
#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;
const int N=504;
int n;
int p[N];
int a[N];
int dp[N];
int main(){
cin>>n;
int i,j;
for(i=1;i<=n;i++){
scanf("%d",p+i);
}
int ans=0x3f3f3f3f;
//枚举环的起点
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
//环确定了起点为i
//于是可以环拉成链
a[j]=p[i+j-1-n*(i+j-1>n)];
}
//求LIS
int len=1;
dp[1]=a[1];
for(j=2;j<=n;j++){
if(a[j]>dp[len]){
dp[++len]=a[j];
}else{
*lower_bound(dp+1,dp+1+len,a[j])=a[j];
}
}
ans=min(n-len,ans);//最小调整次数
}
cout<<ans<<endl;
return 0;
}
E.Bogo Sort(置换+LCM)
题目描述
给出一个置换 \(p\),问 \(1\) ~ \(n\) 这 \(n\) 个数有多少种排列,能经过若干次 \(p\) 的置换变为有序序列。答案对\(10^n\) 取模(\(1\leq n\leq 10^5\))。
分析
在 \(\text{Tonnnny Sort}\) 的 \(\text{shuffle function}\) 中,有操作 \(a_i=b_{p_i}\),实际上是用置换 \(p\) 将原序列 \(a\) 映射到当前的序列 \(a\)。如 \(p=[3,5,4,1,2]\),那么就有:\(a_1=b_3\),\(a_3=b_4\),\(a_4=b_1\),形成了 \(3\to 1\to4\to3\to\cdots\) 的闭环,即 \(a_1,a_3,a_4\) 三者的值进行了交换;同理,有 \(5\to2\to5\to\cdots\) 这样的闭环。
问题转化为:给定置换 \(p\),求多少种排列可以通过置换 \(p\) 完成排序。不妨考虑将排序后的序列 \(a\) 用置换 \(p\) 打乱会产生多少种不同序列。设排序后的序列为 \(a=[a_1,a_2,\cdots,a_n]\),\(p\) 有 \(m\) 个环,且各个环的长度为 \(c_1,c_2,\cdots,c_m\),显然,利用置换 \(p\) 进行 \(\mathrm{lcm}(c_1,c_2,\cdots,c_m)\) 次 \(\text{shuffle function}\),\(a\) 回到最初排完序的状态,而每次操作后得到的序列都是不同的。因此,只要找出置换 \(p\) 所有的环,所有环长的最小公倍数即为答案。
值得注意的是,数据范围较大,可以使用 \(\text{Java}\) 的 \(\text{BigInteger}\) 类。并且,所有环的长度总和为 \(n\),所以所有环的长度的最小公倍数不可能超过 \(10^n\),因此最后不必将答案对 \(10^n\) 取模。
代码
/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第五场) Problem E
Date: 8/20/2020
Description: Group Theory, BigInteger
*******************************************************************/
import java.math.BigInteger;
import java.util.Scanner;
public class Main{
public static void main(String[] args){
final int N=100005;
Scanner in=new Scanner(System.in);
int n=in.nextInt();
BigInteger[] cycle=new BigInteger[N];//环长度
boolean[] vis=new boolean[N];
int[] p=new int[N];
int m=0;
int i;
for(i=1;i<=n;i++){
p[i]=in.nextInt();
}
for(i=1;i<=n;i++){
int len=0;
int pos=i;
while(!vis[pos]){
//遍历环
//记录访问
len++;
vis[pos]=true;
pos=p[pos];
}
if(len>0) cycle[++m]=BigInteger.valueOf(len);
}
BigInteger ans=cycle[1];
//求环长度的最大公约数
for(i=2;i<=m;i++){
ans=cycle[i].multiply(ans).divide(cycle[i].gcd(ans));
}
System.out.println(ans);
}
}
F.DPS(模拟)
题目描述
给出 \(n(1\leq n\leq 100)\) 名玩家的伤害值 \(d_i(0\leq d_i\leq 43962200)\),绘制伤害的直方图(最大值要在图中作出标记),长度为 \(s_i=\lceil50\frac{d_i}{\max\{d_i\}} \rceil\)。
分析
按照题意模拟即可,注意计算 \(s_i\) 时会爆 int。
代码
#include<bits/stdc++.h>
using namespace std;
int a[1010];
int main()
{
int n,maxn=-1;
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
maxn=max(maxn,a[i]);
}
for(int i=1;i<=n;i++)
{
int temp=ceil(50.0*a[i]/maxn);
printf("+");
for(int j=1;j<=temp;j++)
printf("-");
printf("+\n");
if(a[i]!=maxn)
{
printf("|");
for(int j=1;j<=temp;j++)
printf(" ");
printf("|");
printf("%d",a[i]);
puts("");
} else{
printf("|");
for(int j=1;j<=temp-1;j++)
printf(" ");
printf("*|");
printf("%d",a[i]);
puts("");
}
printf("+");
for(int j=1;j<=temp;j++)
printf("-");
printf("+\n");
}
return 0;
}
H.Interval(主席树)
给定一个序列 \(A\),长度为 \(N\),定义函数\(F(l,r)=A_l \& A_{l+1}\&…\&A_r\),集合\(S(l,r)=\{F(a,b)|\min(l,r)\leqslant a\leqslant b\leqslant \max(l,r)\}\),即对 \([l,r]\) 的所有子区间求 \(F\) 的值并去重,有 \(Q\) 次询问,每次询问给出 \(l,r\),求 \(S(l,r)\) 的元素个数。
该题目强制在线,\(L=(L'\oplus lastans) \% N+1\),\(R=(R'\oplus lastans)\%N+1\)。
分析
考虑对于 \(1\) 到 \(N\) 的位置建立普通线段树,维护每个位置出现的不同数字个数。对于序列前 \(x\) 个元素,当查询的区间右界 \(R=x\) 的时候,若 \(F(y,x)=k\),那么对于任意 \(L\leqslant y\) 都满足 \(k\in S(L,x)\),因此对于每一个数字 \(F\) 的值,只要维护它最靠右的出现位置即可,而且对于每一个 \(F\),只能出现在一个位置,不可以重复计数。对于数字的去重,可以通过 unordered_map 来实现。
根据上述分析,查询 \(S(L,R)\) 的时候,需要在 \([1,R]\) 上建立的线段树中查询 \([L,R]\) 的区间,因此需要对每一个位置为区间右界构造线段树,为了更高效,采用主席树来实现。显然,当 \(R=1\) 的时候,整个线段树有且只有一个位置有 \(1\) 的权值,而对于任意 \(R'=R+1\),新的区间的所有 \(F\) 值必然包含原来的区间,因此对 \([1,R]\) 建树的时候所求得的 \(S(1,R)\) 需要进行记录,而对于 \(S(1,R')\),除了包含\(S(1,R)\) 的所有元素以外,还额外包含了\(A_{R'}\) 以及 \(S(1,R)\) 中的所有元素与 \(A_{R'}\) 按位与的结果,将这些新的元素加入 \(S(1,R)\) 去重后即可得到 \(S(1,R')\)。在去重的时候需要始终维护所有数字只保留出现位置最靠后的一个。在主席树创建一个新树的时候,添加的新元素与已经存在的元素发生重复,需要在新树上进行修改,在该元素之前出现的位置进行 update(-1) 的操作,在该元素更新后的位置进行update(1) 的操作,也就是修改其最后出现的位置。
建树完成之后,每次查询只要在 \(root[R]\) 的树上对区间 \([L,R]\) 进行查询即可。
代码
#include<bits/stdc++.h>
#include<unordered_map>
#define mid (l+r)>>1
using namespace std;
const int maxn = 30000005;
int ls[maxn], rs[maxn], val[maxn], root[100005];//左右儿子,权值,主席树的不同根
unordered_map<int, int>mp, la, tmp;//当前树去重得到的元素集合,上一棵树的元素集合,临时辅助集合
int tot;//中结点个数
int newnode(int rt, int v)//动态开点
{
val[++tot] = val[rt] + v;//直接在开点的时候修改权值
ls[tot] = ls[rt];
rs[tot] = rs[rt];
return tot;
}
void update(int& now, int la, int pos, int v, int l, int r)//更新,la代表上一棵树的同位置根节点
{
if (l > pos || r < pos)
return;
now = newnode(la, v);//动态开点
if (l == r)return;
int m = mid;
update(ls[now], ls[la], pos, v, l, m);
update(rs[now], rs[la], pos, v, m + 1, r);
}
int query(int now, int L, int R, int l, int r)//普通二叉树区间查询
{
if (l > R || r < L)return 0;
if (l >= L && r <= R)return val[now];
int m = mid;
return query(ls[now], L, R, l, m) + query(rs[now], L, R, m + 1, r);
}
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
int x;
scanf("%d", &x);
root[i] = root[i - 1];//复制新根
mp[x] = i;//插入新的数字x,位置为i
tmp.clear();
for (auto it : mp)
{
tmp[it.first & x] = max(tmp[it.first & x], it.second);//计算出所有新增F的值,存在tmp中
}
for (auto it : tmp)
{
if (la[it.first] == it.second)continue;//如果某元素已经存在过了,而且位置没有发生改变,就不进行更新
update(root[i], root[i], la[it.first], -1, 1, n);//删去原来的位置
la[it.first] = it.second;//在存放历史树信息的集合中更新数据
update(root[i], root[i], la[it.first], 1, 1, n);//插入在新的位置
}
mp.swap(tmp);//更新mp集合
}
int q;
int lastans = 0;
cin >> q;
while (q--)
{
int l, r;
scanf("%d%d", &l, &r);
l = (l ^ lastans) % n + 1;//强制在线
r = (r ^ lastans) % n + 1;
if (l > r)swap(l, r);
lastans = query(root[r], l, r, 1, n);//查询
printf("%d\n", lastans);
}
return 0;
}
I.Hard Math Problem(数学)
题目描述
有一个 \(n\times m\)的矩阵,以及三个角色:总部、金矿工和收藏家,在矩阵的每个点放置一名角色,要求总部 \(H\) 的旁边至少有一个金矿工 \(G\) 和收藏家 \(E\)。问如何排布能使这种总部数量最多。
分析
用 代表总部,
代表黄金矿工,
代表收藏家,如图的结构能够使总部的数量尽量多。
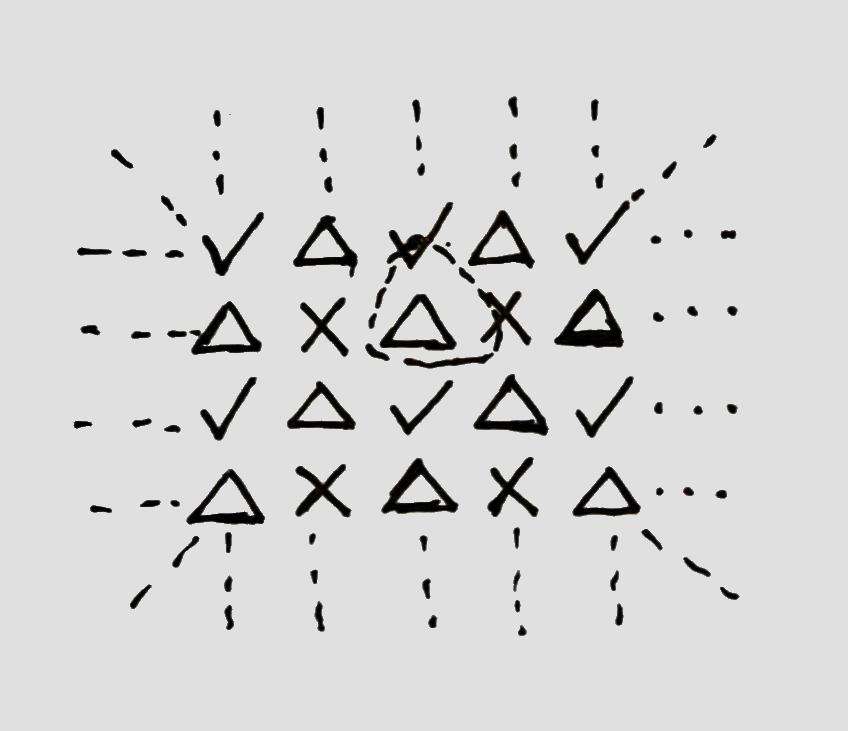
对于一个无穷网络,一个单元已经用虚线框出。一个总部分到 \(\frac{1}{2}\) 个黄金矿工和 \(\frac{1}{2}\) 个收藏家。一个单元所占格子数量为 \(\frac{3}{2}\),一个总部占整个单元的 \(\frac{2}{3}\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号