| Name | Date | Rank | Solved | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020 Multi-University,Nowcoder Day 2 | 2020.7.13 | 139/1162 | 4/11 | Ø | O | O | O | Ø | O | Ø | Ø | Ø | Ø | Ø |
A.All with Pairs(AC自动机/前缀函数+hash)
题目描述
给出 \(n\) 个字符串 \(s_1,s_2,\cdots,s_n\)。定义 \(f(s,t)\) 为串 \(s\) 的前缀与串 \(t\) 的后缀的最大匹配长度。求:
数据范围:\(1\leq n\leq 10^5,1\leq |s_i|,\sum|s_i|\leq 10^6\)。
分析
先把 \(n\) 个串插入AC自动机中,枚举每个字符串作为 \(t\) 串。由于 \(fail[i]\) 含义为所有模式串的前缀中匹配当前节点 \(i\) 的最长后缀,所以每枚举一个字符串 \(t\),\(s\) 串一定在 \(t\) 串结尾字符节点的 \(fail\) 链上,沿 \(fail\) 链统计贡献即可。
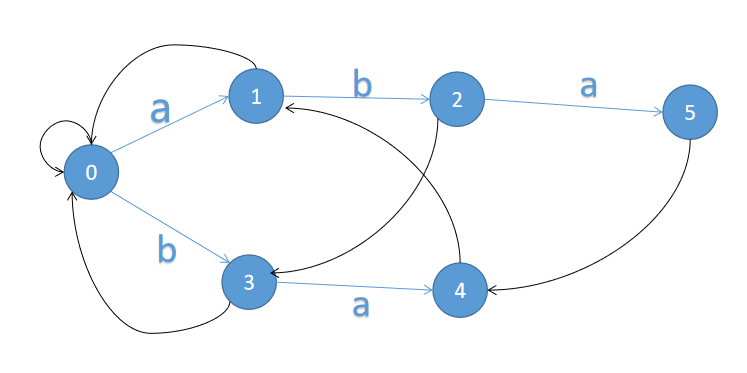
但是对于上图,当前枚举的 \(t\) 串为 \(aba\) 时,在节点 \(5\),贡献为 \(3\times 3\),在节点 \(4\),贡献为 \(2\times 2\),在节点 \(1\),贡献为 \(2\times 1\times 1\),可以发现这里多统计了 $aba $ 的前缀一次贡献,而这个 \(a\) 早在节点 \(5\) 就处理过了,会多算一次。
为了解决这个问题,我们记录每个节点属于哪个字符串。然后枚举 \(t\),匹配 \(s\) 时,每计算完一个字符串的贡献,就用 \(vis[G[j][i]]=1\) 标记上,表示当前位置是 \(s\) 后缀的最长匹配,后面再遇到这个串不进行计算。
代码
#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
const int N=1000100;
char s[N];
int n,trie[N][30],ed[N],fail[N],tot,L[N],vis[N],f[N];
vector<int> G[N];
void insert(char *s,int ID)
{
int p=0,len=strlen(s);
for(int i=0;i<len;i++)
{
int ch=s[i]-'a';
if(trie[p][ch]==0)
trie[p][ch]=++tot;
p=trie[p][ch];
L[p]=i+1;//记录当前节点是字符串的第几个节点
G[p].push_back(ID);//记录哪些字符串中含有当前节点
}
ed[ID]=p;
}
void build()
{
queue<int> Q;
for(int i=0;i<26;i++)
if(trie[0][i])
Q.push(trie[0][i]);
while(!Q.empty())
{
int u=Q.front();
Q.pop();
for(int i=0;i<26;i++)
{
if(trie[u][i]!=0)
{
fail[trie[u][i]]=trie[fail[u]][i];
Q.push(trie[u][i]);
}
else
trie[u][i]=trie[fail[u]][i];
}
}
}
long long dfs(int x)
{
vector<int> temp;
temp.clear();
long long ans=0;
for(int j=x;j;j=fail[j])
{
int sz=G[j].size();
for(int i=0;i<sz;i++)
{
if(!vis[G[j][i]])
{
vis[G[j][i]]=1;
ans=(ans+1ll*L[j]*L[j]%mod)%mod;
temp.push_back(G[j][i]);
}
}
}
for(int i=0;i<temp.size();i++)
vis[temp[i]]=0;
f[x]=ans;//记忆化
return ans;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%s",s);
insert(s,i);
}
build();
long long ans=0;
for(int i=1;i<=n;i++)
{
if(f[ed[i]])//记忆化
ans=(ans+f[ed[i]])%mod;
else
ans=(ans+dfs(ed[i]))%mod;
}
printf("%lld\n",ans);
return 0;
}
分析
计算 \(n\) 个字符串的所有后缀的哈希值,用 \(\text{unordered_map}\) 存不同后缀的个数,\(cnt_x\) 表示哈希值为 \(x\) 的后缀的个数。
然后对每个字符串的前缀求哈希值,若某个前缀的哈希值为 \(x\),那么就有 \(cnt_x\) 个后缀与之匹配,而实际上这样的计数方法会产生重复。就拿单个字符串 \(\mathrm{aba}\) 来说,会有两个后缀 \(\mathrm a\) 和 \(\mathrm{aba}\) 在位置 \(0\) 和 \(2\) 处匹配,而我们要的最长匹配显然是 \(aba\)。也就是说,某个位置 \(i\) 的匹配数多了与 \(i\) 为结尾的前缀与的后缀的最长匹配长度,这就是 \(\text{Next}\) 数组的定义,只需要将位置 \(i\) 的匹配后缀数量减去 \(\text{Next}\) 数组的值就是真正的贡献了。
代码
#include<iostream>
#include<unordered_map>
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
const ull base=131;
const int N=1000003;
const int mod=998244353;
int n;
string s[N];
int Next[N];
//统计不同后缀个数
unordered_map<ull,int>cnt;
int matched[N];
void get_next(string s)
{
int i=0,j=-1;
Next[0]=-1;
while(i<s.length())
{
if(j==-1||s[j]==s[i]) Next[++i]=++j;
else j=Next[j];
}
}
void suffix_countment(string s)
{
ull suffix_hash=0,power=1;
int i;
for(i=s.length()-1;i>=0;i--)
{
suffix_hash+=power*(s[i]-'a'+1);
power*=base;
cnt[suffix_hash]++;
}
}
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;i++)
{
cin>>s[i];
suffix_countment(s[i]);//后缀哈希值
}
ull ans=0;
for(i=1;i<=n;i++)
{
ull prefix_hash=0;
for(j=0;j<s[i].length();j++)//前缀哈希值
{
prefix_hash=prefix_hash*base+(s[i][j]-'a'+1);
matched[j]=cnt[prefix_hash];
}
get_next(s[i]);
//减去重复的
for(j=0;j<s[i].length();j++) matched[Next[j+1]-1]-=matched[j];
//匹配数乘长度的平方
for(j=0;j<s[i].length();j++) ans=(ans+1LL*matched[j]*(j+1)%mod*(j+1)%mod)%mod;
}
cout<<ans<<endl;
return 0;
}
B.Boundary(三角形外心坐标)
题目描述
给出二维平面上 \(n\) 个点的坐标, 求最多有多少个点可以在同一个圆上,原点 \((0,0)\) 也需要在这个圆上(\(1\leq n\leq 2000,|x|,|y|\leq 10000\))。
分析
三点确定三角形外接圆圆心,枚举两个点,求出圆心,统计哪个点作为圆心出现的次数最多。
\((x_0,y_0)\) 代表外接圆圆心坐标,\(r\) 代表外接圆圆心的半径。
代码
#include<iostream>
#include<map>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const double eps=1e-6;
const int N=2005;
int n;
struct CPoint
{
double x;
double y;
bool operator<(const CPoint& A)const
{
if(x==A.x) return A.y-y>eps;
else return A.x-x>eps;
}
}p[N];
map<CPoint,int>cnt;
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
int ans=1;//至少能覆盖一个点
for(i=1;i<=n;i++)
{
cnt.clear();
for(j=i+1;j<=n;j++)
{
//===========================================
//三点确定圆心模板
double x1=0,y1=0;
double x2=p[i].x,y2=p[i].y;
double x3=p[j].x,y3=p[j].y;
double a=x1-x2;
double b=y1-y2;
double c=x1-x3;
double d=y1-y3;
double e=((x1*x1-x2*x2)-(y2*y2-y1*y1))/2;
double f=((x1*x1-x3*x3)+(y1*y1-y3*y3))/2;
if(fabs(b*c-a*d)<eps) continue;
CPoint C;//圆心
C.x=(b*f-d*e)/(b*c-a*d);
C.y=(c*e-a*f)/(b*c-a*d);
//============================================
cnt[C]++;//j1,j2,...,jk
}
//+1 囊括第一层枚举的点
for(auto v:cnt) ans=max(ans,v.second+1);
}
cout<<ans<<endl;
return 0;
}
C.Cover the Tree(思维+dfs序)
题目描述
给一棵 \(n(1\leq n\leq 2\times 10^5)\) 个点的树,用最少的链覆盖每个节点,输出任意一种方案。
分析
每个叶节点都要被覆盖到,假设有 \(cnt\) 个叶节点,则至少需要 \(\lceil\frac{cnt}{2}\rceil\) 条链才能覆盖全部叶节点,同时覆盖其他边。
用 \(\text{dfs}\) 序给每个叶节点编号,以 \(num/2\) 为界,一一对应即可。
代码
#include <bits/stdc++.h>
using namespace std;
vector<int> G[2000010],ans;
int pos[2000010];
int dfs(int x,int fa)
{
for(auto y:G[x])
if(y!=fa)
dfs(y,x);
if(pos[x])
ans.push_back(x);
return 0;
}
int main()
{
int n,cnt=0;
cin>>n;
for(int i=1;i<=n-1;i++)
{
int x,y;
cin>>x>>y;
G[x].push_back(y);
G[y].push_back(x);
}
for(int i=1;i<=n;i++)
{
if(G[i].size()==1)
{
pos[i]=1;
cnt++;
}
}
cout<<(cnt+1)/2<<endl;
dfs(1,0);
int num=ans.size();
for(int i=0,j=num/2;j<num;i++,j++)
cout<<ans[i]<<" "<<ans[j]<<endl;
return 0;
}
D.Duration(模拟)
题目描述
给出两个形如 \(HH:MM:SS(0\leq HH\leq 23,00\leq MM,SS\leq 59)\) 格式的字符串,求时间间隔。
分析
签到。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
int main()
{
tm a, b;
string s1, s2;
cin >> s1 >> s2;
string tmp = s1.substr(0, 2);
a.tm_hour = atoi(tmp.c_str());
tmp = s1.substr(3, 2);
a.tm_min = atoi(tmp.c_str());
tmp = s1.substr(6, 2);
a.tm_sec = atoi(tmp.c_str());
tmp = s2.substr(0, 2);
b.tm_hour = atoi(tmp.c_str());
tmp = s2.substr(3, 2);
b.tm_min = atoi(tmp.c_str());
tmp = s2.substr(6, 2);
b.tm_sec = atoi(tmp.c_str());
a.tm_year = b.tm_year = 100;
a.tm_mon = b.tm_mon = 2;
a.tm_mday = b.tm_mday = 15;
time_t aa, bb;
aa = mktime(&a);
bb = mktime(&b);
ll aaa = aa;
ll bbb = bb;
cout << abs(aaa - bbb) << endl;
return 0;
}
E.Exclusive OR(FWT+线性基)
题目描述
给出 \(n\) 个数,可以重复选择,依次求出选择 \(1,2,\cdots n\) 个数字时的最大异或和(\(1\leq n\leq 2\times 10^5,0\leq A_i<2^{18}\))。
分析
因为所有可选择的数字都小于 \(2^{18}\),所以最大异或和必定小于\(2^{18}\)。那么就有结论,当 取的数字个数 \(i>19\) 时,必定有有 \(ans_{i}=ans_{i-2}\)。下面简单证明:首先,\(\forall\ i\in\mathbb N^\ast\),有 \(ans_{i+2}\geqslant ans_{i}\),只需要在 \(ans_i\) 的基础上随便挑两个相同的数字即可;若 \(i>19\) 且 \(ans_i>ans_{i-2}\),那么异或空间的秩至少为 \(i-1\),这与秩为 \(18\) 矛盾。方便表示,令 \(lim=2^{18}\)。
首先考虑选取两个数字时的答案。对于多项式 \(C=c_0+c_1x+c_2x^2+\cdots+c_{lim-1}x^{lim-1}\), \(c_i>1\) 表示异或和为 \(i\) 的方案存在,否则为 \(0\)。
首先考虑只取两个数字的情况。设多项式 \(A=a_0+a_1x+a_2x^2+\cdots+a_{lim-1}x^{lim-1}\),\(B=b_0+b_1x+b_2x^2+\cdots+b_{lim-1}x^{lim-1}\),初始时,令输入的 \(n\) 个数字的位置的系数为 \(1\)。那么令 \(C=A\oplus B\),即 \(c_i=\sum\limits_{j\oplus k=i}a_j\times b_k\),我们遍历所有 \(c_i\),即可得到能够获得的最大异或和。此时,若 \(c_i>0\),表示取两项能够获得异或和 \(i\),我们同时令 \(b_i=1\)。再算一次 \(A\oplus B\),就能得到取三个数字的最大异或和。迭代 \(19\) 次即可。
代码
/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第二场)Problem E
Date: 9/17/2020
Description: FWT
*******************************************************************/
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long ll;
const int N=(1<<18)+5;
const ll mod=998244353;
const ll inv2=499122177;
const int lim=1<<18;
ll ans[N];
ll A[N],B[N],C[N];
int n;
void FWT_XOR(ll *x,short opt){
for(register int i=1;i<lim;i<<=1){
int step=i<<1;
for(register int j=0;j<lim;j+=step){
for(register int k=0;k<i;k++){
const ll u=x[j+k],v=x[j+k+i];
x[j+k]=u+v;
x[j+k+i]=u-v;
x[j+k]=(x[j+k]%mod+mod)%mod;
x[j+k+i]=(x[j+k+i]%mod+mod)%mod;
if(opt==-1){
x[j+k]=x[j+k]*inv2%mod;
x[j+k+i]=x[j+k+i]*inv2%mod;
}
}
}
}
}
int main(){
cin>>n;
int i,j;
for(i=1;i<=n;i++){
int x;
scanf("%d",&x);
A[x]=B[x]=1;
ans[1]=max(ans[1],(ll)x);
}
FWT_XOR(A,1);
for(i=2;i<=min(19,n);i++){
FWT_XOR(B,1);
for(j=0;j<lim;j++){
C[j]=A[j]*B[j]%mod;
}
FWT_XOR(C,-1);
for(j=0;j<lim;j++){
if(C[j]){
ans[i]=j;
B[j]=1;
}else{
B[j]=0;//一定要初始化!
}
}
}
for(i=20;i<=n;i++){
ans[i]=ans[i-2];
}
for(i=1;i<=n;i++){
printf("%lld",ans[i]);
putchar(i==n?'\n':' ');
}
return 0;
}
F.Fake Maxpooling(单调队列)
题目描述
已知 \(n\times m\) 的矩阵 \(A[i][j]=\text{lcm}(i,j)\),求该矩阵 \(k\times k\) 的最大子矩阵(\(1\leq n,m\leq 5000,1\leq k\leq \min(n,m)\))。
分析
用类似埃式筛的方法在 \(O(nm)\) 的时间内求出每个 \(A[i][j]\)。一次单调队列求出每一行长为 \(k\) 的区间的最大值,另一次单调队列求出列的最大值,求和即为答案。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=5010;
int A[N][N],Q[N];
int main()
{
int n,m,k;
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(A[i][j]==0)
for(int k=1;i*k<=n&&j*k<=m;k++)
A[i*k][j*k]=i*j*k;
for(int i=1;i<=n;i++)
{
int head1=1,tail1=0;
for(int j=1;j<=m;j++)
{
while(head1<=tail1&&A[i][Q[tail1]]<=A[i][j])
tail1--;
Q[++tail1]=j;
if(Q[head1]<=j-k)
head1++;
A[i][j]=A[i][Q[head1]];
}
}
long long ans=0;
for(int j=1;j<=m;j++)
{
int head2=1,tail2=0;
for(int i=1;i<=n;i++)
{
while(head2<=tail2&&A[Q[tail2]][j]<=A[i][j])
tail2--;
Q[++tail2]=i;
if(Q[head2]<=i-k)
head2++;
A[i][j]=A[Q[head2]][j];
if(i>=k&&j>=k)
ans=ans+A[i][j];
}
}
cout<<ans<<endl;
return 0;
}
G.Greater and Greater(bitset)
题目描述
给定长度为 \(n\) 的序列 \(A\) 和长度为 \(m\) 的序列 \(B\),计算 \(A\) 中有多少大小为 \(m\) 的子区间 \(S\),满足 \(\forall i\in \{1,2,\cdots,m\},S_i\geq B_i\)。
数据范围:\(1\leq n\leq 150000,1\leq m\leq \min\{n,40000\},1\leq A_i\leq 10^9,1\leq B_i\leq 10^9\)。
分析
一道利用 \(\text{bitset}\) 的神题。
对每一个 \(b_i\) 求一个长度为 \(n\) 的二进制串 \(x\),\(x_j=1\) 当且仅当 \(a_j\geqslant b_i\)。
对于样例,可以构造三个二进制串:\(\begin{aligned}&a_1\ a_2\ a_3\ a_4\ a_5\ a_6\\b_1=2\ \ \ \ &\ 0\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\\b_2=3\ \ \ \ &\ 0\ \ \ 1\ \ \ 0\ \ \ 1\ \ \ 1\ \ \ 1\\b_3=3\ \ \ \ &\ 0\ \ \ 1\ \ \ 0\ \ \ 1\ \ \ 1\ \ \ 1\end{aligned}\)。设置一个 \(\text{bitset}\ cur\) 来代替二进制串,由于 \(\text{bitset}\) 由低位向高位存储,需要将上述二进制串镜像翻转,即 \(\begin{aligned}&a_6\ a_5\ a_4\ a_3\ a_2\ a_1\\b_1=2\ \ \ \ &\ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 0\\b_2=3\ \ \ \ &\ 1\ \ \ 1\ \ \ 1\ \ \ 0\ \ \ 1\ \ \ 0\\b_3=3\ \ \ \ &\ 1\ \ \ 1\ \ \ 1\ \ \ 0\ \ \ 1\ \ \ 0\end{aligned}\);比如,\(a_2\geqslant b_1\),\(cur_2=1\)。对于一个合法区间,设其起点为 \(k\),则 \(a_k\geqslant b_1,a_{k+1}\geqslant b_2,\cdots,a_{k+m-1}\geqslant b_m\);不妨将上述二进制串的向右平移,得到 \(\begin{aligned}b_1=2\ \ \ \ &\ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 0\\b_2=3\ \ \ \ &\ \ \ \ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 0\ \ \ 1\ \ \ 0\\b_3=3\ \ \ \ &\ \ \ \ \ \ \ \ \ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 0\ \ \ 1\ \ \ 0\end{aligned}\);对于同一列,为 \(a_k\) 与 \(b_1\) 至 \(a_{k+m-1}\) 与 \(b_m\) 的对应大小关系,当且仅当一列有 \(m\) 个 \(1\) 时,存在一个长度为 \(m\) 的合法区间。也就是说,将移动后的 \(m\) 个 \(\text{bitset}\) 进行与运算,最后得到的结果中 \(1\) 的个数即为答案;其中,第 \(i\) 个串右移 \(i-1\) 位。
最暴力枚举获得 \(m\) 个 \(\text{bitset}\) 的时间复杂度为 \(O(mn)\),显然是不可行的。不妨用 pair<int,int> 记录 \(a,b\),\(\text{first}\) 为数值,\(\text{second}\) 为元素在原序列中的位置,接着对 \(a,b\) 按数值降序排列。定义两个 \(\text{bitset}\),用 \(ans\) 记录与运算的最后结果(初始化为全 \(1\));用 \(cur\) 记录 a[j].first>=b[i].first 时,\(a_j\) 在原序列中的位置。接下来提到的 \(a,b\) 中的元素,都为排序后的序列中元素。枚举 \(b_i\),接着枚举 \(a_j\),若 a[j].first>=b[i].first,那么令 cur.set(a[j].second);得到 \(cur\) 后,将 \(cur\) 右移 b[i].second-1 位,同 \(ans\) 进行与运算;多次迭代后,ans.count()即为答案。事实上,经过排序后的序列,不必每次都从 \(1\) 开始枚举 \(a_j\);当枚举 \(b_i\) 时,\(b_{i-1}\) 的数值必然比 \(b_i\) 的数值大,若 a[j].first>=b[i-1].first,必定有 a[j].first>=b[i].first;也就是说,若满足a[j].first>=b[i-1].first的最大的 \(j\) 为 \(x\),考察 \(b_i\) 时,直接从 \(a_{x+1}\) 开始枚举即可,上一次得到的 \(cur\) 中的 \(1\),在此次的考察中一定是正确的,对于 \(a_1\sim a_x\),也是不遗漏的。
/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第二场) Problem G
Date: 8/5/2020
Description: To use bitset
*******************************************************************/
\#include<iostream>
\#include<bitset>
\#include<utility>
\#include<cstdio>
\#include<algorithm>
using namespace std;
const int N=150004;
pair<int,int>a[N],b[N];
int n,m;
bitset<N>ans,cur;
int main()
{
cin>>n>>m;
int i,j;
for(i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
a[i]=make_pair(x,i);
}
for(i=1;i<=m;i++)
{
int x;
scanf("%d",&x);
b[i]=make_pair(x,i);
}
//按数值降序
sort(a+1,a+1+n,[](const pair<int,int>& x,const pair<int,int>& y){return x.first>y.first;});
sort(b+1,b+1+m,[](const pair<int,int>& x,const pair<int,int>& y){return x.first>y.first;});
//初始化
ans.set();
cur.reset();
//枚举 b
for(i=1,j=1;i<=m;i++)
{
//枚举 a
//利用上次信息
while(j<=n&&b[i].first<=a[j].first)
{
cur.set(a[j].second);
j++;
}
//与运算
ans&=cur>>b[i].second-1;
}
cout<<ans.count()<<endl;
return 0;
}
H.Happy Triangle(动态开点线段树)
题目描述
给定一个空多重集,存在三种操作(操作数字均为\(x\)):
\(1.\) 插入一个数字 \(x\) 到多重集中。
$2. $ 在多重集中删除一个数字 \(x\)。
\(3.\) 询问在多重集中是否能找到两个数字 \(a,b\),使 \(a,b,x\) 作为三条边的长度可以构成一个合法的三角形。
一共\(2\times10^5\)次操作,操作数的值域在\([1,10^9]\)。
分析
首先分析三角形构成的条件,对于三角形的三条边\(a,b,c\),存在任意两条边之和大于第三边,令\(a\leqslant b \leqslant c\),可以分别考虑\(x=a\)、\(x=b\)、\(x=c\)三种情况。
\(1.\) 当 \(x=a\) 时,由于 \(c\) 是三条边中的最大值,因此 \(c\) 加上另外两条边中的任意一个,都会大于剩下的一条边,唯一需要满足的条件就是 \(a+b>c\),移项得 \(a>c-b\),由于 \(a\) 是已知量 \(x\),因此我们需要从多重集中寻找\(\min_{a\leqslant b,c}(c-b)_{[1]}\)。
\(2.\) 当 \(x=b\) 的时候,唯一需要满足的条件仍然是 \(a+b>c\),为了尽可能满足该条件,我们需要最大化大于号左侧的值同时最小化大于号右侧的值。显然,实现这一要求的方法就是让 \(a\) 为 \(b\) 也就是 \(x\) 在多重集中的前驱,让 \(c\) 为 \(x\) 在多重集中的后继。如果前驱和后继都存在,且满足不等式,则合法。需要寻找的东西是 \(\{max_{a\leqslant x}a,min_{x\leqslant c}c\}_{[2]}\)。
\(3.\) 当 \(x=c\) 的时候,要最大化不等式左侧的值,显然 \(a,b\) 分别为小于 \(x\) 的最大和次大数字\(_{[3]}\)。
总结上述需要寻找的三个东西,我们实际上需要维护的内容为某个区间的最大值,次大值,最小值,相邻且存在的两个元素的下标差值最小值。
要维护这些东西,很容易联想到线段树,但是值域有 \(10^9\),普通的线段树是开不下的,因此需要运用到动态开点线段树。
动态开点线段树与传统线段树的区别在于,对于每一个节点 \(n\),它的左右子节点并不是 \(n<<1\) 和 \(n<<1|1\),而是作为结点数据域中的一个变量存在的,有点类似于字典树的建树方式。对于某些区间,可能这些区间内并不存在值,因此这些区间的各种要维护的数据也可以认为是一个常量,我们可以规定 \(0\) 号结点作为这些无用结点的代表。在二叉树查询的时候,查询到 \(0\) 结点就可以直接返回了,因为搜索到 \(0\) 号结点已经说明了该子树是一个无用子树,不需要查询。
该题目使用了线段树的单点修改和区间查询,对于区间查询需要有两种,一种查询最大和次大的值,另一种查找相邻存在元素差值最小值,具体看代码:
代码
#include<bits/stdc++.h>
#define mid (l+r)>>1
using namespace std;
struct node//线段树的结点
{
int val;//对于叶节点,维护当前多重集中存在几个该元素
int m1, m2, h1, h2, min;//最小值,次小值,最大值,次大值,相邻差最小值,其中次小值不需要维护,懒得改了
int lson, rson;//存储左右子节点
};
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 200005;
node tree[maxn << 4];
int tot;//计数,已经使用的结点
bool pushup(int n)//向上传递
{
vector<int>vec;
vec.push_back(tree[tree[n].lson].h1);
vec.push_back(tree[tree[n].lson].h2);
vec.push_back(tree[tree[n].rson].h1);
vec.push_back(tree[tree[n].rson].h2);
sort(vec.begin(), vec.end(), greater<int>());
tree[n].h1 = vec[0];
tree[n].h2 = vec[1];//维护最大次大
vec.clear();
vec.push_back(tree[tree[n].lson].m1);
vec.push_back(tree[tree[n].lson].m2);
vec.push_back(tree[tree[n].rson].m1);
vec.push_back(tree[tree[n].rson].m2);
sort(vec.begin(), vec.end());
tree[n].m1 = vec[0];//维护最小次小
tree[n].m2 = vec[1];
tree[n].min = min(tree[tree[n].lson].min, tree[tree[n].rson].min);//维护相邻最小
if (tree[tree[n].rson].m1 != 0x3f3f3f3f && tree[tree[n].lson].h1 != -1)//注意区间合并
{
tree[n].min = min(tree[n].min, tree[tree[n].rson].m1 - tree[tree[n].lson].h1);
}
return vec[0] != inf;//如果左右结点都是空结点,那么该结点也可以进行删除
}
int newnode()//创建新的节点
{
tree[++tot].h1 = tree[tot].h2 = -1;//初始化最大值不存在
tree[tot].min = inf;//相邻差最小值不存在
tree[tot].m1 = tree[tot].m2 = inf;//最小值不存在
tree[tot].lson = tree[tot].rson = 0;//左右儿子均为空
tree[tot].val = 0;
return tot;
}
bool update(int n, int l, int r, int x, int val)
{
if (l == r)
{
tree[n].val += val;
if (tree[n].val != 0)//判断该结点更新数据后是否为空
{
tree[n].h1 = x;//不为空的时候根据个数是否大于1来修改当前结点的数据
tree[n].m1 = x;
if (tree[n].val > 1)tree[n].h2 = x, tree[n].m2 = x, tree[n].min = 0;
else tree[n].h2 = -1, tree[n].m2 = inf, tree[n].min = inf;
return true;
}
else//结点为空特殊处理数据
{
tree[n].min = inf;
tree[n].h1 = tree[n].h2 - 1;
tree[n].m1 = tree[n].m2 = inf;
return false;
}
}
int m = mid;
if (x <= m)
{
if (tree[n].lson == 0)
{
tree[n].lson = newnode();//动态开点
}
if (!update(tree[n].lson, l, m, x, val))tree[n].lson = 0;//如果该次递归返回false说明该子结点已经是空的,可以删除
}
else
{
if (tree[n].rson == 0)
{
tree[n].rson = newnode();
}
if (!update(tree[n].rson, m + 1, r, x, val))tree[n].rson = 0;
}
return pushup(n);
}
pii Max(pii a, pii b)//求最大次大
{
vector<int>vec;
vec.push_back(a.first);
vec.push_back(a.second);
vec.push_back(b.first);
vec.push_back(b.second);
sort(vec.begin(), vec.end(), greater<int>());
return pii(vec[0], vec[1]);
}
pii Min(pii a, pii b)//最小次小
{
vector<int>vec;
vec.push_back(a.first);
vec.push_back(a.second);
vec.push_back(b.first);
vec.push_back(b.second);
sort(vec.begin(), vec.end());
return pii(vec[0], vec[1]);
}
pii query1(int n, int l, int r, int L, int R)//在区间内查找最大和次大的值
{
if (n == 0)return pii(-1, -1);
if (l >= L && r <= R)
{
return pii(tree[n].h1, tree[n].h2);
}
int m = mid;
pii ans(-1, -1);
if (L <= m)
{
ans = Max(ans, query1(tree[n].lson, l, m, L, R));
}
if (R > m)
{
ans = Max(ans, query1(tree[n].rson, m + 1, r, L, R));
}
return ans;
}
pii query2(int n, int l, int r, int L, int R)//查找最小和次小值
{
if (n == 0)return pii(inf, inf);
if (l >= L && r <= R)
{
return pii(tree[n].m1, tree[n].m2);
}
int m = mid;
pii ans(inf, inf);
if (L <= m)
{
ans = Min(ans, query2(tree[n].lson, l, m, L, R));
}
if (R > m)
{
ans = Min(ans, query2(tree[n].rson, m + 1, r, L, R));
}
return ans;
}
int query3(int n, int l, int r, int L, int R)//查找相邻差最小值
{
if (n == 0)return inf;
if (l >= L && r <= R)
{
return tree[n].min;
}
int m = mid;
int ans = inf;
if (L <= m)
{
ans = min(ans, query3(tree[n].lson, l, m, L, R));
}
if (R > m)
{
ans = min(ans, query3(tree[n].rson, m + 1, r, L, R));
}
if (L <= m && R > m)//这里特别注意区间合并
{
if (tree[tree[n].rson].m1 != inf && tree[tree[n].lson].h1 != -1)
ans = min(ans, tree[tree[n].rson].m1 - tree[tree[n].lson].h1);
}
return ans;
}
int main()
{
//freopen("in.in", "r", stdin);
//freopen("ans.out", "w", stdout);
tree[0].h1 = tree[0].h2 = -1;
tree[0].m1 = tree[0].m2 = inf;
tree[0].min = inf;
newnode();
int q;
cin >> q;
while (q--)
{
int op, x;
scanf("%d%d", &op, &x);
if (op == 1)
{
update(1, 1, 1000000000, x, 1);
}
else if (op == 2)
{
update(1, 1, 1000000000, x, -1);
}
else
{
pii l = query1(1, 1, 1000000000, 1, x);
pii r = query2(1, 1, 1000000000, x + 1, 1000000000);
if ((ll)l.first + (ll)l.second > (ll)x)//条件【3】
{
puts("Yes");
continue;
}
int MIN = query3(1, 1, 1000000000, x + 1, 1000000000);
if (x > MIN)//条件【1】
{
puts("Yes");
continue;
}
if (l.first != -1 && r.first != inf)//条件【2】
{
if ((ll)l.first + (ll)x > (ll)r.first)
{
puts("Yes");
continue;
}
}
puts("No");
}
}
return 0;
}
I.Interval(平面图最小割转对偶图最短路)
题目描述
对于一个区间 \([l,r]\),可以进行两种操作:
\(1.\) 收缩,\([l,r]\) 变为 \([l,r-1]\) 或 \([l+1,r]\)。
\(2.\) 扩张,\([l,r]\) 变为 \([l-1,r]\) 或 \([l,r+1]\)。
你有 \(m\) 种四元组 \((l,r,dir,cost)\),可以禁止一些操作。
对于 \((l,r,dir,cost)\) 这个四元组,表示:
-
若 \(dir=L\) 可以花费 \(cost\) 禁止 \([l,r]\) 到 \([l+1,r]\)。
-
若 \(dir=R\) 可以花费 \(cost\) 禁止 \([l,r]\) 到 $[l,r+1] $。
对于区间 \([1,n]\),求出最小的花费,使得所有 \(l\neq r\),如果不可能,输出 \(-1\)。
数据范围:\(2\leq n\leq 500,0\leq m\leq n(n-1),1\leq cost\leq 10^6\)。
分析
把区间 \([l,r]\) 看作二维平面上的一个点 \((l,r)\),其中源点为 \((1,n)\),汇点为 \((n,1)\)。之后把所有 \((i,i)\) 的点与汇点连一条流量为 \(+\infty\) 的边,没有被限制的两点之间也连一条流量为 $ +\infty$ 的边(实际上由于转成对偶图最短路之后,两点间的距离为 $ +\infty $,所以在代码中通过不建边来体现两点之间无法直接到达)。
最后平面图最小割转对偶图最短路,时间复杂度 \(O(n^2\log n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=510*510;
const long long INF=0x3f3f3f3f3f3f3f3f;
int n,m,S,T;
int head[N],num_edge;
long long dist[N];
bool vis[N];
struct Edge
{
int to;
int dis;
int Next;
}edge[N<<2];
void add_edge(int from,int to,int dis)
{
edge[++num_edge].to=to;
edge[num_edge].dis=dis;
edge[num_edge].Next=head[from];
head[from]=num_edge;
edge[++num_edge].to=from;
edge[num_edge].dis=dis;
edge[num_edge].Next=head[to];
head[to]=num_edge;
}
priority_queue<pair<int,int> > Q;
void Dijkstra()
{
memset(dist,INF,sizeof(dist));
memset(vis,0,sizeof(vis));
dist[S]=0;
Q.push(make_pair(0,S));
while(!Q.empty())
{
int x=Q.top().second;
Q.pop();
if(vis[x])
continue;
vis[x]=1;
for(int i=head[x];i;i=edge[i].Next)
{
int y=edge[i].to,z=edge[i].dis;
if(dist[y]>dist[x]+z)
{
dist[y]=dist[x]+z;
Q.push(make_pair(-dist[y],y));
}
}
}
}
int main()
{
cin>>n>>m;
S=0;T=n*n+1;
for(int i=1;i<=m;i++)
{
int l,r,cost;
char dir[2];
scanf("%d %d %s %d",&l,&r,dir,&cost);
if(dir[0]=='L')
{
if(r==n)
add_edge((l-1)*(n-1)+r-1,T,cost);
else
add_edge((l-1)*(n-1)+r-1,(l-1)*(n-1)+r,cost);
}
else
{
if(l==1)
add_edge(S,(l-1)*(n-1)+r-1,cost);
else
add_edge((l-1)*(n-1)+r-1,(l-2)*(n-1)+r-1,cost);
}
}
Dijkstra();
if(dist[T]!=INF)
cout<<dist[T]<<endl;
else
puts("-1");
return 0;
}
J.Just Shuffle(置换群的幂)
题目描述
已知单位置换 \(e=\pmatrix{1&2&3&\cdots&n\\1&2&3&\cdots&n}\) 变换 \(k\) 次后可以得到置换 \(A=\pmatrix{1&2&3&\cdots&n\\A_1&A_2&A_3&\cdots&A_n}\),求 \(e\) 变换一次后得到的置换 \(B\)(\(1\leq n\leq 10^5,10^8\leq k\leq 10^9\),\(k\) 是质数)。
分析
\(k\) 是大质数,即 \(\gcd(n,k)=1\),这个条件保证循环不会分裂。
已知 \(B^k=A\),等式两边同时置换 \(z\) 次,变为 \(B^{k\times z}=A^z\),当 \(k\times z\mod len=1\) (\(len\) 为置换循环节的长度)时,有 \(B=A^z\),把 \(A\) 置换 \(z\) 次即可。
把 \(A\) 所有环都求出来,设这些环长的大小分别为 \(r_1,r_2,\cdots\),对每一个 \(r_i\) 求一个逆元 \(inv_i=k^{-1}\pmod {r_i}\),把 \(A\) 中的每个环都转 \(inv_i\) 次,即可得到 \(B\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int vis[N],A[N],B[N];
vector<int> vec;
int main()
{
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++)
scanf("%d",&A[i]);
for(int i=1;i<=n;i++)
{
if(!vis[i])
{
vec.clear();
int x=A[i];
while(!vis[x])
{
vis[x]=1;
vec.push_back(x);
x=A[x];
}
int len=vec.size(),inv;
for(int i=0;i<=len-1;i++)
if(1ll*k*i%len==1)
inv=i;
for(int i=0;i<=len-1;i++)
B[vec[i]]=vec[(i+inv)%len];
}
}
for(int i=1;i<=n;i++)
printf("%d ",B[i]);
puts("");
return 0;
}
K.Keyboard Free(积分)
题目描述
给定三个同心圆,半径分别为 \(r_1,r_2,r_3(1\leq r_1,r_2,r_3\leq 100)\),在三个圆上分别选择一点,求这三点组成的三角形的面积的期望值。
分析
由于 \(S_{\triangle ABC}\) 只与 \(A,B,C\) 三点的相对位置有关,可以将 \(A\) 视作顶点,\(B,C\) 为动点。不妨以同心圆的圆心作为原点建立平面直角坐标系,令 \(A(r_1,0)\),\(B(r_2\cos\alpha,r_2\sin\alpha)\),\(C(r_3\cos\beta,r_3\sin\beta)\);\(\alpha,\beta\in\mathbb R\),且 \(0\leqslant\alpha,\beta\leqslant 2\pi\)。
利用向量的叉积计算面积
设出现极角 \(\alpha,\beta\) 的概率为 \(f(\alpha,\beta)\),则 \(S_{\triangle ABC}\) 的期望为
此题精度要求较低,不妨将 \(2\pi\) 分成 \(t\) 份,每份的角度为 \(\frac{2\pi}{t}\),那么 \(f(\alpha,\beta)=\frac{1}{t^2}\)。可直接用矩形法求积分的近似数值解,设置步长为 \(\frac{2\pi}{t}\),枚举 \([0,2\pi]\) 内的所有角度即可。
代码
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第二场) Problem K
Date: 8/4/2020
Description: Expectation and Integral
*******************************************************************/
\#include<iostream>
\#include<cstdio>
\#include<algorithm>
\#include<cmath>
using namespace std;
const int t=400;
const double pi=acos(-1);
double _sin[t+1],_cos[t+1];
int main()
{
int i,j,_;
const double step=2*pi/t;
double theta=0;
for(i=1;i<=t;i++)
{
_sin[i]=sin(theta);
_cos[i]=cos(theta);
theta+=step;
}
for(cin>>_;_;_--)
{
double r1,r2,r3;
scanf("%lf%lf%lf",&r1,&r2,&r3);
//=====================
//排序
if(r1>r2) swap(r1,r2);
if(r2>r3) swap(r2,r3);
if(r1>r3) swap(r1,r3);
//=====================
//矩形法
//枚举 t*t 个角度组合
double ans=0;
for(i=1;i<=t;i++)
{
for(j=1;j<=t;j++)
{
ans+=fabs((r2*_cos[i]-r1)*r3*_sin[j]-(r3*_cos[j]-r1)*r2*_sin[i]);
}
}
printf("%.1lf\n",ans/2/t/t);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号