| Name | Date | Rank | Solved | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020 Multi-University,Nowcoder Day 1 | 2020.7.12 | 101/1216 | 3/10 | Ø | Ø | × | Ø | × | O | × | Ø | O | O |
A.B-Suffix Array(后缀数组+结论)
题目描述
给出一个长为 \(n\) 字符串 \(s\),定义字符串 \(s_1\) ~ \(s_n\) 对应的 \(B_1\) ~ \(B_n\) 满足 \(B_i=\min\limits_{1\leq j < i,s_j=s_i}\{i-j\}\),如果不存在这样的 \(j\),那么 \(B_i=0\),将 \(s\) 的所有后缀按照其对应的 \(B\) 序列的字典序排列并输出。
多组输入,字符集只包括 \(a,b\),\(1\leq n\leq 10^5\)。
分析
定义 \(C_i=\min\limits_{i<j\leq n,s_j=s_i}\{j-i\}\)。对于不存在 \(j\) 的 \(C_i\),使它比其他 \(C_i\) 都大,即设 \(C_i=n\),最后再把 \(n+1\) 这个数字放在 \(C\) 序列的结尾,求出 \(C\) 的后缀数组,去掉最后一位倒着输出就是答案。
证明
\(B_i\) 相当于当前位置 \(i\) 前面最近的一个与 \(s_i\) 相同的字符到 \(i\) 的距离,而 \(C_i\) 相当于当前位置 \(i\) 后面的最近的与 \(s_i\) 相同的字符到 \(i\) 的距离。
\(1.\) 首先考虑一种特殊情况。
对于后缀 \(aaaab\cdots\),其 \(B\) 数组开头的一段为 \([0,1,1,1,0,\cdots]\),两个 \(0\) 代表第一次出现的 \(a\) 字符和 \(b\) 字符。
考虑两个 \(0\) 中间连续 \(1\) 子序列的长度,它的长度越长,字典序就越大,比如对于后缀 \(X=aaab\) 和 \(Y=aaaab\) ,其 \(B\) 数组分别为 \([0,1,1,0]\),\([0,1,1,1,0]\),显然后者的字典序更大。
考虑这两个后缀的 \(C\) 数组,分别为 \([1,1,4,4,5]\) 和 \([1,1,1,5,5,6]\),可以发现前者的字典序更大。
也就是说,对于开头的 \(1\) 长度不同的两个后缀,如果后缀 \(X\) 的 \(B\) 数组比后缀 \(Y\) 的 \(B\) 数组字典序小,则后缀 \(X\) 的 \(C\) 数组一定比后缀 \(Y\) 的 \(C\) 数组的字典序大。
\(2.\) 接下来考虑一般情况。
假设两个后缀 \(X,Y\) 的 \(B\) 数组有一段前缀是相同的,那么 \(X,Y\) 的这一段前缀一定也是相同的,假设这段公共前缀是若干个 \(a\),那么肯定满足 \(X=\cdots aaab\cdots,Y=\cdots aaaab\cdots\)。
他们的 \(B\) 数组分别为:\([z,1,1,x,\cdots]\),\([z,1,1,1,y,\cdots]\)。所以后缀 \(X\) 的 \(B\) 数组的字典序比后缀 \(Y\) 的 \(B\) 数组的字典序大。
考虑它们的 \(C\) 数组,相当于把 \(B\) 数组的每个字符与其前面第一个相同的字符对齐,\(C\) 数组分别为 \([z,1,1,x,\cdots],[z,1,1,y,\cdots]\)。
可以发现,\(x,y\) 之前的位都是相同的,也就是说,\(x,y\) 之间的大小关系决定了这两个后缀的字典序。对于一开始 \(x,y\) 的位置,可以发现 \(x\) 那个位置离上一个 \(b\) 更近一些,即满足 \(x<y\),所以后缀 \(X\) 的 \(C\) 数组的字典序比后缀 \(Y\) 的 \(C\) 数组的字典序要小。
综合上述两种情况,可以知道,对于两个后缀 \(X,Y\),假如 \(X\) 的 \(B\) 数组的字典序比 \(Y\) 的 \(B\) 数组的字典序要小,那么总有 \(X\) 的 \(C\) 数组的字典序比 \(Y\) 的 \(C\) 的字典序要大。
由数学归纳法可知,求出 \(C\) 数组的后缀数组再反过来就是答案。
证毕。
仔细思考可以发现,\(C\) 数组相对于 \(B\) 数组的优越性在于:字符串某个后缀的 \(C\) 数组一定是这个字符串的 \(C\) 数组的某个后缀,所以求出 \(C\) 的后缀数组,就相当于将原字符串的后缀进行排序了。而 \(B\) 数组不满足这个性质,对于字符串的某个后缀,它的 \(B\) 数组不一定是原字符串的 \(B\) 数组的后缀,所以不能直接后缀排序。
为什么末尾要放一个 \(n+1\)?
假如末位是 \(ab\),对应两个后缀 \(ab,b\),它们的 \(B\) 数组分别为 \([0,0],[0]\),所以 \(b\) 的 \(B\) 数组字典序比 \(ab\) 的 \(B\) 数组字典序小,那么 \(b\) 的字典序比 \(ab\) 小;而我们最后要将 \(C\) 数组的 \(sa\) 数组倒序输出,也就是说,在倒序之前,\(b\) 的 \(C\) 数组的字典序比 \(ab\) 的 \(C\) 数组的字典序要大。
但是事实上 \(b\) 的 \(C\) 数组为 \([2]\),\(ab\) 的 \(C\) 数组为 \([2,2]\),即 \(b\) 的 \(C\) 数组字典序比 \(ab\) 小,在 \(C\) 数组末尾加一个 \(n+1\) 就可以解决这个问题。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1000010;
char s[N];
int n,m,w,C[N];
int sa[N],rk[N<<1],oldrk[N<<1],ID[N],px[N],cnt[N];
bool cmp(int x,int y,int w)
{
return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w];
}
void SA(int n,int m,int *s)
{
m=n;
for(int i=1;i<=n;i++)
{
rk[i]=s[i];
cnt[rk[i]]++;
}
for(int i=2;i<=m;i++)
cnt[i]=cnt[i]+cnt[i-1];
for(int i=n;i>=1;i--)
{
sa[cnt[rk[i]]]=i;
cnt[rk[i]]--;
}
int p;
for(w=1;w<n;w<<=1,m=p)
{
p=0;
for(int i=n;i>n-w;i--)
ID[++p]=i;
for(int i=1;i<=n;i++)
if(sa[i]>w)
ID[++p]=sa[i]-w;
for(int i=1;i<=m;i++)
cnt[i]=0;
//memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;i++)
{
px[i]=rk[ID[i]];
cnt[px[i]]++;
}
for(int i=1;i<=m;++i)
cnt[i]=cnt[i]+cnt[i-1];
for(int i=n;i>=1;--i)
{
sa[cnt[px[i]]]=ID[i];
cnt[px[i]]--;
}
for(int i=1;i<=n;i++)
swap(rk[i],oldrk[i]);
//memcpy(oldrk,rk,sizeof(rk));
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)
{
if(cmp(sa[i],sa[i-1],w))
rk[sa[i]]=p;
else
rk[sa[i]]=++p;
}
if(p==n)
break;
}
}
int main()
{
while(~scanf("%d",&n))
{
scanf("%s",s+1);
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(s[i]==s[j])
{
C[i]=j-i;
break;
}
}
if(C[i]==0)
C[i]=n;
}
C[n+1]=n+1;
SA(n+1,m,C);
for(int i=n;i>=1;i--)
printf("%d ",sa[i]);
puts("");
for(int i=1;i<=n+1;i++)
C[i]=sa[i]=rk[i]=oldrk[i]=ID[i]=px[i]=cnt[i]=0;
}
return 0;
}
B.Infinite Tree(虚树+换根dp求重心)
题目描述
给定一棵无向无边权的无限结点的树,其结点编号从 \(1\) 到正无穷,对于 \(i(i>1)\) 号结点,存在一条边连向\(\displaystyle{\frac{i}{mindiv(i)}}\) 号结点(\(mindiv(i)\) 代表 \(i\) 的最小质因子 ),第 \(i!\) 号结点存在权值 \(w_i\)。选取任意结点作为根,给定m,求 \(1\) ~ \(m\) 中的所有整数 \(i\),\(i!\) 结点到根结点的简单路径距离与 $ w_i$ 的乘积和的最小值。
换句话说,定义\(\delta(u,v)\) 为结点 \(u,v\) 之间简单路径的距离,求 \(\displaystyle{\min_u\sum^{m}_{i=1}w_i\delta(u,i!)}\)。
数据范围:\(1\leqslant m\leqslant 10^5, 0\leqslant w_i \leqslant 10^4 ,\sum_{m}\leqslant10^6\)。
分析
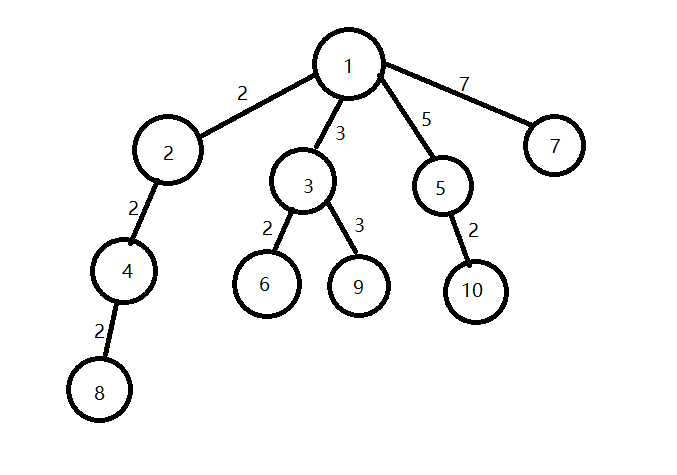
这是 \(1\) 到 \(10\) 号结点的图的构成,每条边上的数字是它连接的两个结点相除的结果,注意这里边上的数字并非边权,该题中所有边都认为是 \(1\) 的长度。
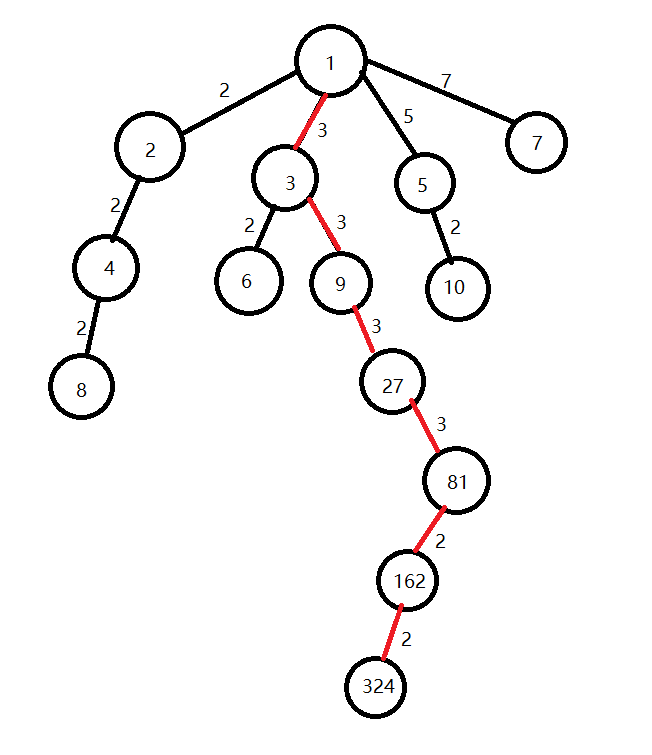
上图中红色的路径为 \(3\rightarrow 2\rightarrow 4\) 号结点到 \(1\) 号结点的简单路径,可以看到:
\(1.\) 假设 \(1\) 为树的根的时候,任何数字到根结点的简单路径中,每一条边连接两点相除的结果就是这个数字进行质因子分解所得到的字典序最小的质因子序列。
\(2.\) 假设 \(1\) 为根,每一个结点的子结点都是自身乘以一个小于等于自身的质数。
\(3.\) 结点的深度为自身的质因子个数。
两个结点的LCA可以认为是两个结点编号的质因子序列的后缀乘积。
首先剔除掉题目中选择 \(i!\) 结点这个条件,题意变为,每个结点都有其权值,求该树的带权重心。这里带权中心的定义就是选取一个根,使所有结点到根的简单路径的距离与该结点的权值乘积的和最小,符合这个条件的根就是该树的重心。
在求带权重心的时候,可以使用两次 \(\text{dfs}\) 进行换根求解,首先以 \(1\) 号结点为根,求出每个结点的子树大小,由于该题目中,树的结点是存在权值的,因此在计算子树大小的时候,每一个结点的贡献应该为其权值。第一次\(\text{dfs}\) 的时候还需要求出所有点到根节点的简单路径与权值的乘积(之后写作 \(ans\))。
在第二次 \(\text{dfs}\) 的时候,每走一步都假设将根从前一个结点转移到了下一个结点,而 \(ans\) 的值也会变化。由于之前以 \(1\) 为根处理过整棵树的 \(size\),而 \(dfs\) 也是以 \(1\) 为根的前序遍历,因此每一次的换根都是从父亲结点转移到孩子结点的,相当于新的根中所有的结点都顺着这条边往回走了一步,而除了该子树以外的所有结点都顺着这条边往新的结点走了一步,假设这一条边是从 \(u\) 走到了 \(v\),则 \(ans\) 的变化值也就可以用 \(dp[u]+(size[1]-size[v])-size[v]\),其中 \(dp\) 用于换根过程中每一个结点为根计算得的 \(ans\)。
换根代码:
void dfs(int x)
{
dp[x] = 0;
siz[x] = Val[x];
for (auto it : vec[x])
{
dfs(it.to);
dp[x] += dp[it.to] + siz[it.to] * it.val;
siz[x] += siz[it.to];
}
}
ll ans = 0x7fffffffffffffff;
void ddfs(int x, ll change)
{
dp[x] = change;
ans = min(ans, dp[x]);
for (auto it : vec[x])
{
ddfs(it.to, (dp[x] + it.val * (siz[1] - siz[it.to] - siz[it.to])));
}
}
对于该题目,只有编号为某个整数的阶乘的时候才会有权值,那么我们就可以把其他点的权值设置为 \(0\) 即可。考虑如下情况:
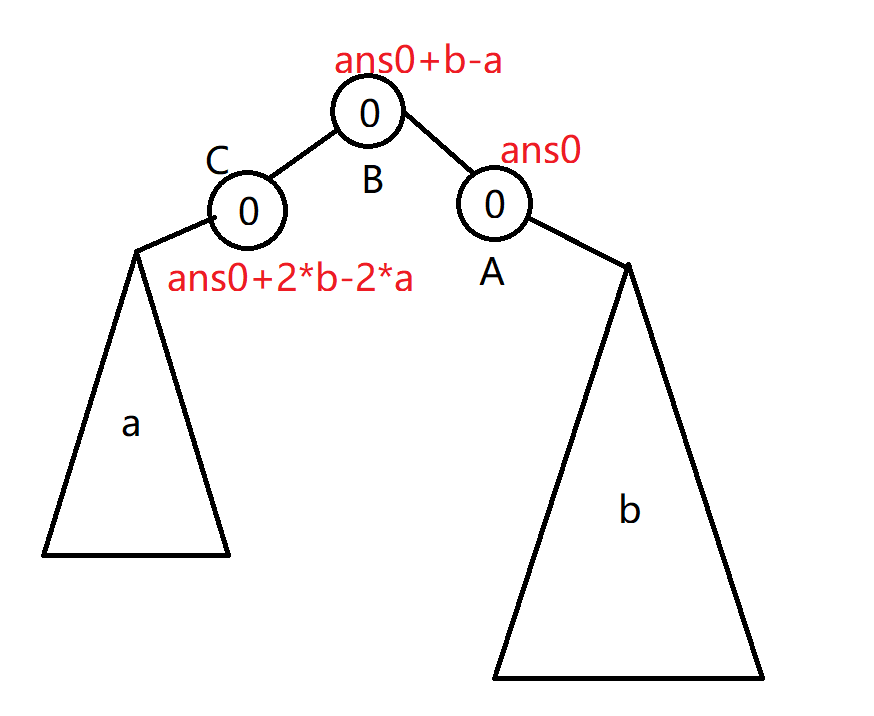
\(size\) 分别为 \(a\) 和 \(b\) 的两棵子树由 \(A,B,C\) 三个权值为 \(0\) 的结点所连接,那么以 \(A\) 结点为 \(ans0\) 的话,那么\(B,C\) 两个结点的权值可以推为 \(ans0 + b - a\) 和 \(ans0 + 2 * b - 2 * a\) ,可以得出权值在 \(A\) 到 \(C\) 这条路径上是单调的,或者全部为相同的值,那么最终,这个重心必然会位于 \(a\) 或 \(b\) 这两棵子树中(或者子树中以及 \(A,B,C\) 三个点全部都是重心)。
由此,我们可以认为这棵树的重心可能由很多个,而这些重心可能存在与权值为 \(0\) 的结点,其中至少有一个必然存在于权值不为 \(0\) 的结点。这也就符合了构建虚树的条件:选择原树上的一些点为关键点,其他的点不会影响到问题的答案。
该题目中,可能存在的最大结点编号为\(10^5!\),属于天文级别的数字,但是如果构建虚树,只会有至多 \(2\times 10^5\) 个点。
构造虚树的核心在于预处理 \(\text{LCA}\) 和 \(\text{dfs}\) 序,但是由于这棵原树的体积庞大,这两个东西都无法使用正常方法进行求解,因此需要该题进行特殊处理。
首先对于 \(\text{dfs}\) 序,该题目中给出来的关键点编号分别为 \(1!,2!,3!,\cdots\) ,那么后一个数字的质因子必然包含前一个数字的所有质因子。对于原树的结构进行分析,如果对每个结点的子节点按照其需要乘的数字大小为关键字排序的话,得到的 \(\text{dfs}\) 序即路径上每个边代表的数字的字典序,对于某一个质因子,后一个数字所包含的该质因子的个数只可能大于或者等于前一个数字的,因此其质因子序列必然是字典序递增的,回归到树上也就是本身就保证了\(\text{dfs}\) 序。
\(\text{LCA}\) 的求解需要使用到之前所推出来的一个结论:
两个结点的 \(\text{LCA}\) 可以认为是两个结点编号的质因子序列的后缀乘积,那么这个 \(\text{LCA}\) 的深度也就是两个结点的质因子序列后缀长度。
两个核心问题都解决之后,继续讨论虚树构建中存在的问题:
由于原先的树体积非常大,无法正常存储,只能单纯以数学方法求其数据,而不会在程序中真实存在,因此要在构建虚树的时候动态创建树的结点。
在虚树中,大量的非重要结点都被删除掉了,但是实际上在这些非重要结点上,\(ans\) 也是在变化的。由于这些结点权值为 \(0\),变化可以认为是与 经过的边数线性相关 的,因此,这些非关键点在删除的时候,应该保留它们的边,也就是将虚树中的边变成带有权值的边,用以代表之前被删除掉的非重要结点。
之前得到,以 \(1\) 为根的时候,每个结点的深度可以认为是其分解质因子的个数,那么可以根据这个规则求出每个边的长度。考虑连接边的情况:从一号结点连接到任何结点,边权为该结点深度。连接两个非根节点,边权为两个结点的深度差值。我们可以首先用筛法加速,对前 \(m\) 个数字进行质因子分解,紧接着通过前缀和求出每一个关键结点的质因子个数,并记录为其深度。由于建立虚树需要使用相邻两两之间的 \(\text{LCA}\),因此对每一对相邻关键节点求其 \(\text{LCA}\) 的深度。之前说到 \(\text{LCA}\) 的深度是两个结点编号的质因子序列后缀长度,而后一个结点的质因子序列相当于在前一个结点的质因子序列中插入一些数字,设插入的数字中最大的数字是 \(max\),那么插入前后的序列最长公共后缀就是原序列中以第一个 \(max\) 为起点的后缀。
例如: 2 2 2 2 3 3 3 3 5 中插入2 2 3,则 \(max\) 值为3,插入前后的序列比较为:
很显然,最长公共后缀为第二个序列中红色数字之后的部分,也就是原序列中以第一个 \(max\) 为开头的后缀。
得到这个结论后,就可以数据结构维护每个数字出现的次数,求得要插入数字的 \(max\) 后,\(deep[LCA(i,i-1)]=sum[10^5]-sum[max-1]\),其中 \(sum\) 数组代表前 \(i\) 个质因子出现次数的前缀和。为了优化时间,这里使用树状数组对前缀和进行维护。
在顺序递推关键结点的深度同时,也要递推第 \(i\) 个结点和 \(i-1\) 结点的 \(\text{LCA}\) 的深度,以便随后使用。在构建虚树的时候,不再使用 \(\text{dfs}\) 序作为出栈的判断,而是以深度作为出栈的判断。
至此,虚树建立完成。在虚树上求一下带权重心即可。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node//邻接数组中存的边
{
int to;
int val;
};
const int maxn = 100005;
vector<node>vec[maxn << 1];//存放图
int LCA[maxn];//存放LCA下标
int dep[maxn << 1];//存放关键点深度,前1e5个位置存放关键点深度,后面的是LCA的深度
ll w[maxn];//输入
ll dp[maxn << 1];//换根时存放ans
ll siz[maxn << 1];//子树大小
ll Val[maxn << 1];//点权
//////////////////////////////欧拉筛//////////////////////////////////////////
int prime[maxn];//筛法加速分解质因子
int visit[maxn];
int m;
void Prime()
{
for (int i = 2; i <= maxn; i++)
{
if (!visit[i]) {
prime[++prime[0]] = i; //纪录素数, 这个prime[0] 相当于 cnt,用来计数
}
for (int j = 1; j <= prime[0] && i * prime[j] <= maxn; j++) {
visit[i * prime[j]] = 1;
if (i % prime[j] == 0) {
break;
}
}
}
}
void init()
{
Prime();
int tityz = 0;
}
//////////////////////////////树状数组//////////////////////////////////////////
int a[maxn], c[maxn]; //对应原数组和树状数组
int lowbit(int x)
{
return x & (-x);
}
void updata(int i, int k)
{ //在i位置加上k
while (i <= maxn)
{
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i)
{ //求A[1 - i]的和
int res = 0;
while (i > 0)
{
res += c[i];
i -= lowbit(i);
}
return res;
}
//////////////////////////////预处理LCA和深度//////////////////////////////////////////
int zyz[1005];//存放质因子
int num[1005];//质因子出现次数
void getdep()
{
dep[2] = 1;
LCA[2] = 0;
updata(1, 1);
for (int i = 3; i < maxn; i++)//分解质因子并在树状数组中更新
{
int tmp = i;
int cnt = 0;
int MAX = 0;//维护出现的最大的质因子在zyz数组中的下标
if (!visit[i])
{
for (int j = 1;; j++)
{
if (prime[j] == i)
{
MAX = j;
zyz[cnt] = j;
num[cnt++] = 1;
break;
}
}
}
else
{
for (int j = 1; prime[j] * prime[j] <= i; j++)
{
int tt = prime[j];
if (tmp % tt == 0)
{
zyz[cnt] = j;
num[cnt] = 0;
while (tmp % tt == 0)
{
tmp /= tt;
num[cnt]++;
}
cnt++;
MAX = j;
}
}
if (tmp != 1)
{
for (int j = 1;; j++)
{
if (prime[j] == tmp)
{
MAX = j;
zyz[cnt] = j;
num[cnt++] = 1;
break;
}
}
}
}
LCA[i] = getsum(maxn) - getsum(MAX - 1);//求LCA深度
for (int j = 0; j < cnt; j++)//更新树状数组
{
updata(zyz[j], num[j]);
}
dep[i] = getsum(maxn);
}
for (int i = 1; i < maxn; i++)//更新所有点的深度和LCA的对应位置
{
dep[maxn + i] = LCA[i];
LCA[i] = maxn + i;
}
}
//////////////////////////////换根求解//////////////////////////////////////////
void add(int u, int v, int val)//加边
{
vec[u].push_back(node{ v ,val });
}
int st[maxn];//手写栈
void dfs(int x)//预处理子树大小,起点的ans值
{
dp[x] = 0;
siz[x] = Val[x];
for (auto it : vec[x])
{
dfs(it.to);
dp[x] += dp[it.to] + siz[it.to] * it.val;
siz[x] += siz[it.to];
}
}
ll ans = 0x7fffffffffffffff;
void ddfs(int x, ll change)//换根求解
{
dp[x] = change;
ans = min(ans, dp[x]);
for (auto it : vec[x])
{
ddfs(it.to, (dp[x] + it.val * (siz[1] - siz[it.to] - siz[it.to])));
}
}
int main()
{
//预处理
Prime();
getdep();
while (scanf("%d", &m) != EOF)
{
for (int i = 1; i <= m; i++)
scanf("%lld", &w[i]);
//建树
int tot = 0;
vec[1].clear();
Val[1] = w[1];
int top = 0;
st[++top] = 1;
for (int i = 2; i <= m; i++)
{
int lca = LCA[i];
if (dep[lca] != dep[st[top]])//使用深度代替dfs序来维护单调栈
{
while (dep[st[top - 1]] > dep[lca])
{
add(st[top - 1], st[top], dep[st[top]] - dep[st[top - 1]]);
top--;
}
if (dep[lca] != dep[st[top - 1]])
{
vec[lca].clear();
add(lca, st[top], dep[st[top]] - dep[lca]);
st[top] = lca;
}
else
{
add(st[top - 1], st[top], dep[st[top]] - dep[lca]);
top--;
}
}
vec[i].clear();//每次加入某个点时进行清空
Val[i] = w[i];
st[++top] = i;
}
for (int i = 1; i < top; i++)
{
add(st[i], st[i + 1], dep[st[i + 1]] - dep[st[i]]);
}
//////////////////////////////////////
//求解
dfs(1);
ans = 0x7fffffffffffffff;
ddfs(1, 1, dp[1]);
printf("%lld\n", ans);
/*for (int i = 1; i < maxn * 2; i++)
{
if (!vec[i].empty())
{
printf("%d: ", i);
for (auto it : vec[i])
{
printf("%d ", it);
}
putchar('\n');
}
}*/
//////////////////////////////////////
}
return 0;
}
/*
1
2
6
24
120 60 30 15 5
720 360 180 90 45 15 5
5040 2520 1260 630 315 105 35 7
40320 20160 10080 5040 2520 1260 630 315 105 35 7
362880 181440 90720 45360 22680 11340 5670 2835 945 315 105 35 7
3628880 1814400 907200 453600 226800 113400 56700 28350 14175 4725 1575 525 175 35 7
*/
D. Quadratic Form(线性代数+矩阵求逆)
题目描述
给定 $ n\times n$ 的实正定二次型矩阵 \(A\) 和 \(n\) 维向量 \(b\),求当 \(\displaystyle\sum\limits_{i = 1}^n \sum\limits_{j = 1}^n A_{ij} x_i x_j \leq 1\),即 \(x^TAx\leq 1\) 时,\(\displaystyle\sum\limits_{i = 1}^n b_i x_i\) 的最大值。
数据范围:\(1\leq n\leq 200,0\leq |A_{ij}|,|b_i|\leq 10^9,A_{ij}=A_{ji}\),\(n\) 的总和不超过 \(10^4\)。
分析
将题目转化为约束条件下的最值问题。此处只讨论极值,不讨论边界可能存在的最值。
考虑到约束条件 \(\sum\limits_{i = 1}^n \sum\limits_{j = 1}^n a_{ij} x_i x_j \leqslant 1\) 为不等式约束,可以添加 \(\mathrm{KKT}\) 条件,利用拉格朗日乘数法求解。
首先需要讨论矩阵 \(A\) 的一些性质。由于 \(\mathrm{det}(A) \not\equiv 0 \pmod {998244353}\),故 \(A\) 可逆。根据 \(a_{ij}\in\mathbb Z\) 且 \(a_{ij}=a_{ji}\),得 \(A\) 为实对称矩阵,继而 \(A^{-1}\) 也为实对称矩阵。又有 \(\sum\limits_{i = 1}^n \sum\limits_{j = 1}^n a_{i j} x_i x_j > 0\),故 \(A\) 为正定矩阵,继而 \(A^{-1}\) 也为正定矩阵。上述性质都会在接下来的推导中涉及。
定义:\(x=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}\),\(b=\begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}\)。 则有约束条件 \(x^TAx\leqslant1\),要求最大值的表达式为 \(x^Tb\) 或 \(b^Tx\)。
令 \(L(x_1,x_2,\cdots,x_n,\lambda)=\sum\limits_{i=1}^n b_ix_i+\lambda\left(\sum\limits_{i=1}^n\sum\limits_{j=1}^{n}a_{ij}x_ix_j-1\right)\);有 \(\mathrm{KKT}\) 方程组如下。
将 \(\mathrm{KKT}\) 方程组的第一式展开,得到如下方程组。
将上述方程组写成矩阵形式,有 \(b+2\lambda Ax=0\)。即 \(\lambda x=-\frac{1}{2}A^{-1}b\ (1)\),等式两边取转置,得 \(\lambda x^T=-\frac{1}{2}b^TA^{-1}\ (2)\);\((2)\times A\times(1)\),得 \(\lambda^2x^TAx=\frac{1}{4}b^TA^{-1}b\)。代入约束条件,移项后有 \(x^TAx\le 1\), \(\lambda^2\ge\frac{1}{4}b^TA^{-1}b\);由于 \(A^{-1}\) 为正定矩阵,故 \(\lambda\ge\frac{1}{2}\sqrt{b^TA^{-1}b}>0\);所以约束条件是有效的,即 \(x^TAx=1\ (3)\)。根据式 \((1),(2)\),可得到最优解为 \(x=-\frac{1}{2\lambda}A^{-1}b,x^T=-\frac{1}{2\lambda}b^TA^{-1}\);将其带入式 \((3)\),有 \(\frac{1}{4\lambda^2}b^TA^{-1}b=1\ (*)\)。
由于 \(\sum\limits_{i=1}^nb_ix_i=b^Tx\),代入最优解 \(x=-\frac{1}{2\lambda}A^{-1}b\),得 \(\sum\limits_{i=1}^nb_ix_i\) 的最大值为 \(-\frac{1}{2\lambda}b^TA^{-1}b\)。于是,\(\left(\sum\limits_{i=1}^nb_ix_i\right)^2\) 最大值为 \(\frac{1}{4\lambda^2}\left(b^TA^{-1}b\right)^2\);将式 \((*)\) 代入,有 \(\frac{1}{4\lambda^2}\left(b^TA^{-1}b\right)^2=b^TA^{-1}b\)。
综上所述,最终答案为 \(b^TA^{-1}b\bmod 998244353\)。套用矩阵求逆模板和矩阵乘法公式即可。
代码
/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第一场) Problem D
Date: 7/22/2020
Description:
Use lagrange multiplier method
Compute the inverse matrix
*******************************************************************/
#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const int N=202;
const ll mod=998244353;
ll a[N][N<<1],b[N],c[N];
int n;
void inverse();
ll qpow_mod(ll a,int b);
int main()
{
while(~scanf("%d",&n))
{
int i,j,k;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
scanf("%lld",&a[i][j]);
a[i][n+j]=0;//初始化
a[i][j]%=mod;
}
}
for(i=1;i<=n;i++)
{
scanf("%lld",b+i);
b[i]%=mod;
}
inverse();
//=========================================
//a[1][1+n]*b[1]+a[2][1+n]*b[2]...
//a[2][1+n]*b[1]+a[2][1+n]*b[2]...
//...
for(j=1;j<=n;j++)
{
ll res=0;
for(i=1;i<=n;i++)
{
res+=a[i][j+n]*b[i];
res%=mod;
}
c[j]=res%mod;
}
//c存b的转置由乘A的结果
//==========================================
//计算c右乘B
ll ans=0;
for(i=1;i<=n;i++)
{
ans+=b[i]*c[i];
ans%=mod;
}
//==========================================
printf("%lld\n",ans);
}
return 0;
}
void inverse()//矩阵求逆模板
{
int m=n+n;
int i,j,k;
for(i=1;i<=n;i++) a[i][i+n]=1;
for(i=1;i<=n;i++)
{
for(j=i;j<=n;j++)
{
if(a[j][i])
{
for(k=1;k<=m;k++)
{
swap(a[i][k],a[j][k]);
}
}
}
ll r=qpow_mod(a[i][i],mod-2);
for(j=i;j<=m;j++) a[i][j]=r*a[i][j]%mod;
for(j=1;j<=n;j++)
{
if(i==j) continue;
ll rate=a[j][i]*a[i][i]%mod;
for(k=i;k<=m;k++)
{
a[j][k]=a[j][k]-rate*a[i][k]%mod;
a[j][k]=(a[j][k]%mod+mod)%mod;
}
}
}
}
ll qpow_mod(ll a,int b)
{
ll res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
F.Infinite String Comparision(模拟)
题目描述
对于字符串 \(x\),定义 \(x^{\infty}\) 为 \(xxx\cdots\)。给出两个字符串 \(a,b\),判断 \(a^{\infty}\) 和 \(b^{\infty}\) 的字典序大小关系(\(1\leq |a|,|b|\leq 2\times 10^5\))。
分析
把两个串都复制一遍,逐字符比较字典序大小即可。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s1, s2;
while (cin >> s1 >> s2)
{
int ans = 0;
int len1 = s1.size(), len2 = s2.size();
int len = max(s1.size(), s2.size());
for (int i = 0; i < 2 * len; i++)
{
char ch1 = s1[i % len1], ch2 = s2[i % len2];
if (ch1 < ch2)
{
ans = -1;
break;
}
if (ch1 > ch2)
{
ans = 1;
break;
}
}
switch (ans)
{
case -1:puts("<"); break;
case 0:puts("="); break;
case 1:puts(">"); break;
default:
break;
}
}
return 0;
}
H.Minimum-cost Flow(费用流)
题目描述
给定一张 \(n\) 个点 \(m\) 条边的网络,每条边都有一个费用 \(c_i\)。\(q\) 次询问,每次询问给出 \(u_i\) 和 \(v_i\),表示每条边的容量都为 \(u_i/v_i\)(保证 \(\leq 1\)),当图中的流量为 \(1\) 时,求此时的最小费用。
数据范围:多组输入,\(2\leq n\leq 50\),\(1\leq m\leq 100\),\(1\leq a_i,b_i\leq n\),\(1\leq c_i\leq 10^5\),\(1\leq q\leq 10^5\),\(0\leq u_i\leq v_i\leq 10^9\),\(v_i\geq 0\),\(m\) 的总和不超过 \(10^4\),\(q\) 的总和不超过 \(10^6\)。
分析
由于边的容量为一个分数 \(\frac{u}{v}\),总流量为 \(1\)。先扩大 \(\frac{v}{u}\) 倍,将每条边的容量固定为 \(1\),此时即求流量为 \(\frac{v}{u}\) 时的最小费用。用 \(\text{SPFA}\) 寻找增广路,找到一条路径时,此路径的流量一定为 \(1\),且得到的路径的费用为当前网络中的最低费用。每次找到增广路并计算费用时,将每次得到的路径的费用用 \(\text{map}\) 记录下来。
对于每次询问,将流量分解,从 \(\text{map}\) 中取值,每次取出一条路径来提供一个单位的流量,直到流量满足要求。
由于 \(1\leq u,v\leq 10^9\),看似最坏情况需要遍历 \(10^9\) 次才能得到答案。但是由于图中每条边的容量都是 \(1\),所以对于每一条路径,它只有满流和零流两种情况;而且边数最多 \(100\) 条,即最大流不超过 \(100\) 个单位,最多遍历 \(100\) 次,时间复杂度为 \(100\times 10^5=10^7\)。当 \(maxflow\ast u<v\) 时无解,输出 \(NaN\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=200010,M=10010;
struct Edge
{
int to;
long long dis;
long long cost;
int Next;
}edge[M];
int head[N],num_edge=1,n,m,s,t;
long long maxflow,mincost;
map<long long,long long> mp;
void add_edge(int from,int to,int dis,int cost)
{
edge[++num_edge].to=to;
edge[num_edge].dis=dis;
edge[num_edge].cost=cost;
edge[num_edge].Next=head[from];
head[from]=num_edge;
}
bool vis[N];
long long dis[N],incf[N];
int pre[N];
bool SPFA()
{
queue<int> Q;
for(int i=1;i<=n;i++)
dis[i]=INF;
memset(vis,0,sizeof vis);
Q.push(s);
vis[s]=1;
dis[s]=0;
incf[s]=1<<30;
while(!Q.empty())
{
int x=Q.front();
Q.pop();
vis[x]=0;
for(int i=head[x];i;i=edge[i].Next)
{
if(!edge[i].dis)
continue;
int y=edge[i].to;
if(dis[y]>dis[x]+edge[i].cost&&edge[i].dis)
{
dis[y]=dis[x]+edge[i].cost;
pre[y]=i;
incf[y]=min(incf[x],edge[i].dis);
if(!vis[y])
{
Q.push(y);
vis[y]=1;
}
}
}
}
if(dis[t]==INF)
return false;
return true;
}
void update()
{
int x=t;
while(x!=s)
{
int i=pre[x];
edge[i].dis-=incf[t];
edge[i^1].dis+=incf[t];
x=edge[i^1].to;
}
maxflow+=incf[t];
mincost+=dis[t]*incf[t];
mp[dis[t]*incf[t]]+=incf[t];
}
int main()
{
while(cin>>n>>m)
{
memset(head,0,sizeof head);
memset(pre,0,sizeof(pre));
num_edge=1;
maxflow=0,mincost=0;
mp.clear();
for(int i=1;i<=m;i++)
{
int a,b;long long c;
scanf("%d %d %lld",&a,&b,&c);
add_edge(a,b,1,c);
add_edge(b,a,0,-c);
}
s=1,t=n;
while(SPFA())
update();
int q;
cin>>q;
while(q--)
{
long long u,v;
scanf("%lld %lld",&u,&v);
long long x=0,y=v;
if(maxflow*u<v)
puts("NaN");
else
{
map<long long,long long>::iterator it;
for(it=mp.begin();it!=mp.end();it++)
{
if(v>it->second*u)
{
v=v-it->second*u;
x=x+it->first*u;
}
else
{
x=x+it->first*v/it->second;
break;
}
}
long long gcd=__gcd(x,y);
printf("%lld/%lld\n",x/gcd,y/gcd);
}
}
}
return 0;
}
I.1 or 2(一般图最大匹配)
题目描述
给一张 \(n\) 个点 \(m\) 条边(\(1\leq n\leq 50,1\leq m\leq 200\))以及每个点的度 \(d_i\) 的无向图,选择一些边满足点的度要求,若能满足输出 \(Yes\),反之输出 \(No\)。
分析
拆度+拆边建图,举例说明,对于下图,\(d_i=[1,2,1,0]\)。
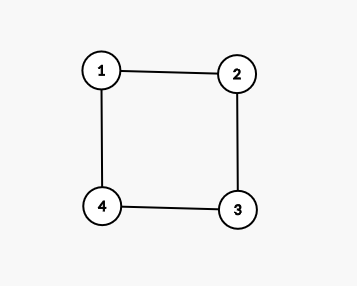
按照度数将原图中的点 \(1\) 拆成 \(1\),点 \(2\) 拆成 \(2,3\),点 \(3\) 拆成 \(4\)。
再将原图的每条边都拆成两个点并连接,即:
对于原图中的边,将 每个度的拆点与其对应边的拆点相连,在新图中的连接情况如下:
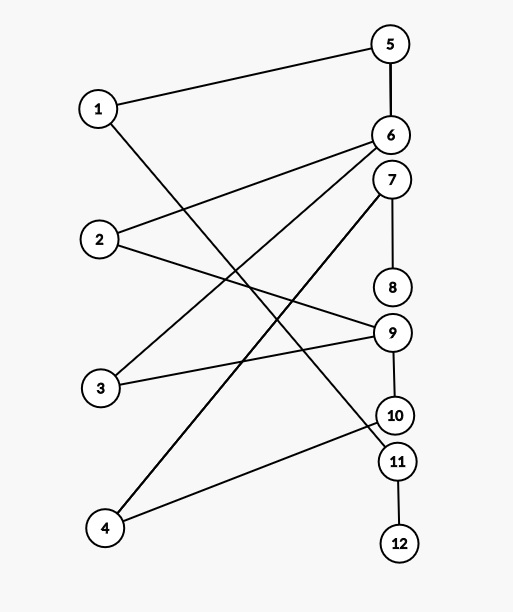
建完图后求一般图最大匹配数,如果是 完备匹配,代表可以满足度的要求。
比如上图,最大匹配为 \((1,5),(2,6),(3,9),(4,10),(7,8),(11,12)\)。
如果达到完备匹配,某条边的另一端必定匹配着另一个点的一个度,表示拆点与原点相连,这样一条边的匹配是合乎要求的。
例如上图中 \((1,5),(2,6)\) 就是原图中点 \(1\) 的一个度连接原图点 \(2\) 的一个度,\((3,9),(4,10)\) 就是原图点 \(2\) 的一个度连接原图点 \(3\) 的一个度。
而 \((7,8),(11,12)\) 代表删除原图中的边 \((3,4),(1,4)\),保留原图的边 \((1,2),(2,3)\)。
对于每条边而言,其匹配只有两种情况,第一种是,一条边两端的度拆出来的两个点分别和原图中的边拆出来的两个点匹配,这样代表了这条边需要留在原图中;另一种情况是,原图中的边拆出来的两个点相互匹配,代表着这条边在原图中应该被删除。
#include<bits/stdc++.h>
using namespace std;
struct Edge
{
int to;
int Next;
}edge[250010];
int head[5010],num_edge;
void add_edge(int from,int to)
{
edge[++num_edge].to=to;
edge[num_edge].Next=head[from];
head[from]=num_edge;
}
int ID[1010][1010];
int x[5010],y[5010],d[5010];
int match[5010];//match[i]代表点i的匹配点
int pre[5010];//pre[i]代表点i的前驱节点
int fa[5010];//代表点i的祖先节点
int vis[5010];//vis[i]=0代表点i未被染色,vis[i]=1代表点i为黑色,vis[i]=2代表点i为白色
int dfn[5010];//dfn[x]=cnt代表点x向上跳时的标记
int cnt;
int n,m,ans;
int get(int x)
{
if(x==fa[x])
return x;
return fa[x]=get(fa[x]);
}
int LCA(int x,int y)//寻找两个节点的花根
{
cnt++;//每次LCA选用不同的cnt作为判断条件
x=get(x);y=get(y);//用并查集找祖先,只处理祖先节点
while(dfn[x]!=cnt)//若某一个点被标记两次,即为花根LCA
{
dfn[x]=cnt;//给点x标记
x=get(pre[match[x]]);//沿着match和pre向上
if(y!=0)
swap(x,y);//x,y交替向上
}
return x;
}
queue<int> Q;
void blossom(int x,int y,int w)//以点w为花根,将花缩成花根一点,并建立内部的反向pre
{
while(get(x)!=w)//已经到达花根,说明开花完成
{
pre[x]=y;//增广路取反
y=match[x];
if(vis[y]==2)//如果y点是白点,但花中所有点都是黑点
{
vis[y]=1;//把白点染黑
Q.push(y);//加入队列中
}
if(get(x)==x)//跳的过程中,暴力把所有访问到的节点和花的并查集全部合并到w(LCA)上,表示它们的花根是w(LCA)
fa[x]=w;
if(get(y)==y)
fa[y]=w;
x=pre[y];//增广路取反
}
}
int bfs(int S)
{
for(int i=1;i<=n;i++)//初始化
{
fa[i]=i;
vis[i]=0;
pre[i]=0;
}
while(!Q.empty())
Q.pop();
Q.push(S);//起点S加入对列
vis[S]=1;//S染黑
while(!Q.empty())
{
int x=Q.front();
Q.pop();
for(int i=head[x];i;i=edge[i].Next)
{
int y=edge[i].to;
if(get(x)==get(y)||vis[y]==2)//如果x和y已经在同一个花中或者y是白点(这意味着y已经有匹配点),这种情况不会增加匹配数,直接跳过
continue;
if(!vis[y])//如果点y没有被染色
{
vis[y]=2;//先把y染成白色
pre[y]=x;//然后将y的前驱点记为x
if(!match[y])//如果点y没有被匹配过,直接匹配成功
{
for(int p=y,last;p;p=last)//增广路取反
{
last=match[pre[p]];
match[p]=pre[p];
match[pre[p]]=p;
}
return 1;
}
vis[match[y]]=1;//如果点y已经被匹配过,则把与y匹配的点染成黑色,并加入队列中
Q.push(match[y]);
}
else//vis[y]=1,代表点y是黑色,形成奇环,需要将环缩成一点(开花)
{
int w=LCA(x,y);
blossom(x,y,w);
blossom(y,x,w);
}
}
}
return 0;
}
int main()
{
//int T,kase=0;
//cin>>T;
while(cin>>n>>m)
{
num_edge=0;
cnt=0;
memset(ID,0,sizeof(ID));
memset(match,0,sizeof(match));
memset(head,0,sizeof(head));
memset(dfn,0,sizeof(dfn));
//cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d",&d[i]);
for(int i=1;i<=m;i++)
scanf("%d %d",&x[i],&y[i]);
int tot=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=d[i];j++)
ID[i][j]=++tot;
for(int i=1;i<=m;i++)
{
add_edge(tot+1,tot+2);
add_edge(tot+2,tot+1);
for(int j=1;j<=d[x[i]];j++)
{
add_edge(ID[x[i]][j],tot+1);
add_edge(tot+1,ID[x[i]][j]);
}
for(int j=1;j<=d[y[i]];j++)
{
add_edge(tot+2,ID[y[i]][j]);
add_edge(ID[y[i]][j],tot+2);
}
tot=tot+2;
}
n=tot;
ans=0;
for(int i=1;i<=n;i++)
if(!match[i])
ans=ans+bfs(i);
if(ans*2==n)
puts("Yes");
else
puts("No");
}
return 0;
}
J.Easy Integration(积分/规律)
题目描述
给定数字 \(n(1\leq n\leq 10^6)\),求 \(\displaystyle\int_0^1(x−x^2)^n\text{ d}x\)。
分析
令 \(I=\displaystyle\int_0^1(x−x^2)^n\text{ d}x=\displaystyle\int_0^1 x^n(1−x)^n\text{ d}x\),利用分部积分法求解。
预处理阶乘后,只需要计算逆元即可得到答案。
或者处理还原样例输出的逆元,发现分别是 \(\frac{1}{6},\frac{1}{30},\frac{1}{140}\),查询 \(\text{OEIS}\):A002457。
代码
#include <bits/stdc++.h>
using namespace std;
long long fac[2000010];
const long long mod=998244353;
long long quick_pow(long long a,long long b)
{
long long ans=1;
while(b)
{
if(b&1)
ans=ans*a%mod;
a=a*a%mod;
b=b>>1;
}
return ans;
}
long long C(long long n,long long m)
{
if(m>n)
return 0;
return fac[n]*quick_pow(fac[m],mod-2)%mod*quick_pow(fac[n-m],mod-2)%mod;
}
int main()
{
fac[0]=1;
for(int i=1;i<=2000005;i++)
fac[i]=fac[i-1]*i%mod;
long long n;
while(scanf("%lld",&n)!=EOF)
{
printf("%lld\n",quick_pow(C(2*n+1,n+1)*(n+1)%mod,mod-2));
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号