2020/03/04 协方差、特征向量的统计意义理解与图像分布的理解

理解协方差

方差
首先，我们设\(X\)表示随机变量，它的观测样本是\((x_{1}, x_{2}, ..., x_{i}, ...)\)。有了观测样本，我们可以计算出观测样本的平均值\(\bar{x}\)。进一步，我们可以利用公式：
\(\sigma_{x}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\)
求出该随机变量\(X\)的方差。由公式我们可以看出，方差是用来度量随机变量和其数学期望（即均值）之间的偏离程度。

协方差
现在我们增加一个随机变量\(Y\)，它的观测样本是\((y_{1}, y_{2}, ..., y_{i}, ...)\)。随机变量\(Y\)的观测样本均值为\(\bar{y}\)。这个时候我们可以定义两个随机变量的__协方差__为：
\(\sigma(x, y)=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)\)
协方差是用来衡量两个随机变量之间的变化方向关系。例：

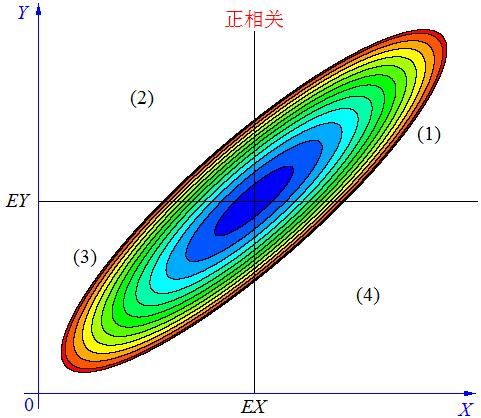
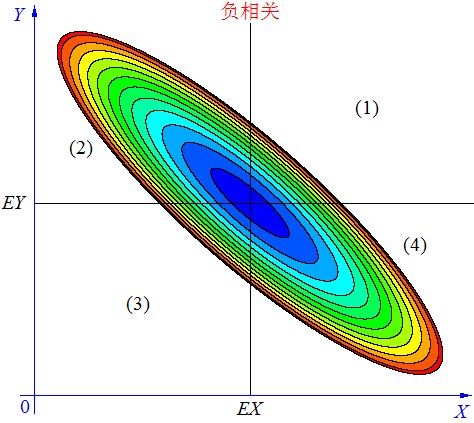
以上图转载自：CSDN-GoodShot

特征向量统计意义

想象一下我们有一个数量为\(N\)的苹果图片数据集，我们用特征提取器得到能对每张图片提取一个长度为d维的特征向量 （d维： □□□□...□）。我们可以认为每个维度都是一个随机变量\(x_{k}, 其中k\in(1,2,...,d)\)。
对于第\(i\)张图片，特征向量每个维度都有相应的值，对应到统计里可以认为是第\(i\)个观测样本值。
□   □   □   ... □   ... □   ...   □  第1个样本
□   □   □   ... □   ... □   ...   □  第2个样本
......
□   □   □   ... □   ... □   ...   □  第i个样本
\(x_{1,i}\) \(x_{2,i}\) \(x_{3,i}\) ... \(x_{k,i}\) ... \(x_{m,i}\) ... \(x_{d,i}\)
......
□   □   □   ... □   ... □   ...   □  第\(N\)个样本

这样，各个维度之间的协方差：
\(\sigma\left(x_{m}, x_{k}\right)=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{m i}-\bar{x}_{m}\right)\left(x_{k i}-\bar{x}_{k}\right)\)

反映在batch的矩阵操作上是这样的：

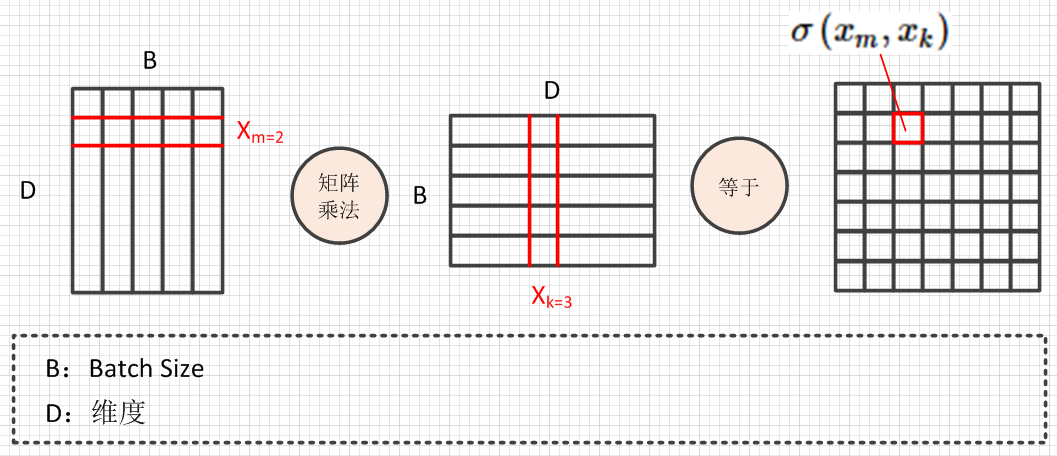
vsd_file

参考文章：| 如何直观地理解「协方差矩阵」 |

计算机视觉中，图像分布的理解

图片的每个像素位置我们也能够认为是随机变量，它们分别服从一定的分布。

我们假设某个像素位置为随机变量\(Z\)，它服从高斯分布
\(p(z)=\frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-(z-\bar{z})^{2} / 2 \sigma^{2}}\)，
它的概率密度分布如图所示

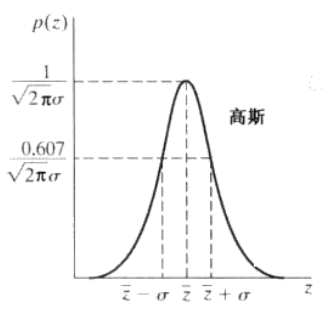
这就表示该像素的值有70%的概率落在\([(\bar{z}-\sigma),(\bar{z}+\sigma)]\)
参考:mysee1989

多元高斯分布例子：吴恩达斯坦福笔记
多元高斯分布的由来： 知乎-清雅的机器学习笔记
主要证明思路：1. 从一元标准正态分布（均值0，方差1）推广到 n 个独立标准正态分布。2.进而用\(\vec x\)的线性变换推广到一般。