2019/12/30 贝叶斯估计、最大似然估计、最大后验概率估计
问题:这些估计都是干嘛用的?它们存在的意义的是什么?
有一个受损的骰子,看起来它和正常的骰子一样,但实际上因为受损导致各个结果出现的概率不再是均匀的 \(\frac{1}{6}\) 了。我们想知道这个受损的骰子各个结果出现的实际概率。准确的实际概率我们可能永远无法精确的表示出了,但是我们可以通过做大量实验来尽可能地近似它。我们可以掷很多次骰子,然后统计一下 \(\frac{各个结果出现的次数}{总掷骰子的次数}\) 这个比例作为各个结果的概率,这个概率就作为我们对这个骰子各个结果概率的估计值。
上面其实就是一个 概率分布估计 的例子。现实中很多规律是我们很难预先了解的,但我们可以观测到在这个规律下产生的数据(样本),我们希望能够通过这些已经观测到的样本来推测或者估计出这个规律以达到帮助我们掌握规律的目的。
我们可以数学化一下上面的例子。我们可以掷骰子的结果看成是一个随机变量\(X\)。我们假设观测的数据 \(\{x_{1}, ..., x_{N}\}\) 是由 \(P(X|\theta)\) 这个分布产生,其中 \(\theta\) 是某个分布的参数,它是一个变量,是我们要估计的量。最大似然估计、最大后验概率估计以及贝叶斯估计就是帮助我们估计这个参数 \(\theta\) 的方法。
给定一组观测样本 \(X=\{x_{1}, ..., x_{N}\}\),最大似然估计、最大后验概率估计以及贝叶斯估计就是要估计产生这组样本的分布模型。
做个说明
- \(P(X)\):样本先验。比如投硬币,直觉经验告诉我们正反面概率应该各为0.5
- \(P(X|\theta)\):参数似然。就是实验观测结果,比如通过分别统计实际样本中正反面出现的频率发现 正面概率0.7,反面概率0.3(与直觉不同)。
估计方法pipline
所有估计方法的 第一步 就是要先对样本的联合概率分布 \(P(x_{1}, ..., x_{N}|\theta)\) 做出假设。比如我们假设 \(P(x_{1}, ..., x_{N}|\theta)=f(\theta, \{x_{1}, ..., x_{N}\})\),其中 \(f\) 是分布函数(比如高斯函数, \(f=Gauss()\) ),\(f\) 的输入是 \(\theta\) 和 \(\{x_{1}, ..., x_{N}\}\);\(\theta\) 是分布 \(f\) 的参数,它是我们实际要估计的东西。
最大似然估计
- \(\theta\) 是一个定值
- 通过 \(\arg \max _{\Theta} P(x_{1}, ..., x_{N}|\theta)\) 实现求\(\theta\)。
由于\(x_{1}, ..., x_{N}\)独立同分布。 \(\arg \max _{\theta} P(x_{1}, ..., x_{N}|\theta) = \arg \max _{\theta} P(x_{1}|\theta) \cdot P(x_{2}|\theta) \cdot ... \cdot P(x_{N}|\theta)\)
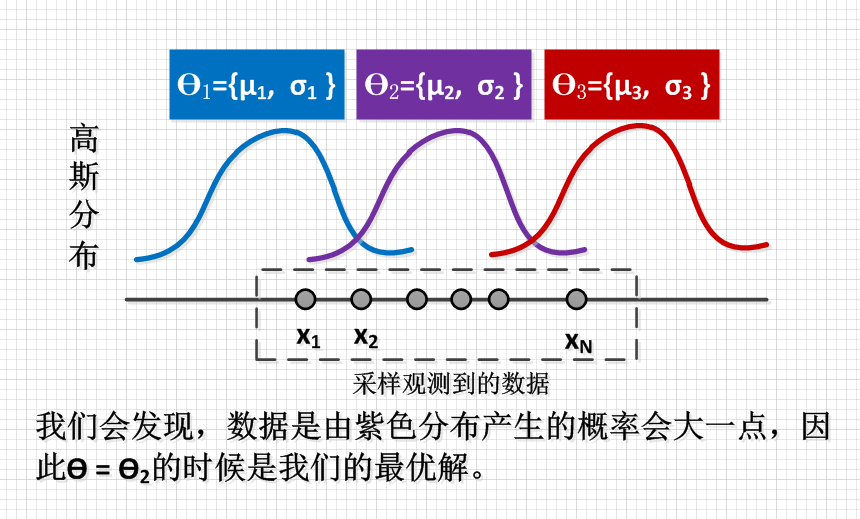
直观的解释就是,找到最合适的 \(\theta\),使得现在观测到的样本出现的概率最大。
vsd文件
\(P(x_{N}|\theta)\)是参数的 似然,表示观测样本是由 \(\theta\)确定的分布 生成的情况下,看到样本x_{N}的概率。一般情况下,\(P(x_{N}|\theta)=某个分布函数(x_{N}, \theta)\)
最大后验概率
- \(\theta\) 是一个随机变量,它有取值范围 \(\theta \subset (\theta_{1}, \theta_{2}, \theta_{3},...)\)
- 通过 \(\arg \max _{\theta} P(\theta|x_{1}, ..., x_{N})\) 实现求\(\theta\)。
根据贝叶斯准则\(P\left(B_{i} \mid A\right)=\frac{P\left(B_{i}\right) P\left(A \mid B_{i}\right)}{P(A)}\)
由于\(x_{1}, ..., x_{N}\)独立同分布。 \(\arg \max _{\theta} P(\theta|x_{1}, ..., x_{N})=\arg \max _{\theta} P(x_{1}, ..., x_{N}|\theta) \cdot P(\theta)=\arg \max _{\theta} P(\theta) \cdot \prod_{n=1}^{N} P(x_{n}|\theta)\)
直观的解释现在还不能理解,等以后理解了再补充。
\(P(\theta=\theta_{1}|x_{N})\)是参数的 后验概率,表示观测样本是\(x_{N}\)的情况下,\(\theta=\theta_{1}\)的概率。
贝叶斯估计
- \(\theta\) 是一个随机变量,它有取值范围 \(\theta \subset (\theta_{1}, \theta_{2}, \theta_{3},...)\)
- 通过求后验分布的期望\(\theta = E[P(\theta|x_{1}, ..., x_{N}]\) 实现求\(\theta\)。即求在观测样本是\((x_{1}, ..., x_{N})\)的情况下,\(\theta\)取值的期望。
直观的解释现在还不能理解,等以后理解了再补充。
一些说明:
- 实际上,随机变量\(X\)的分布用\(P(X)\)来表示是不严谨的,通常,对于离散型随机变量,我们通常用 分布律函数 来表示随机变量取值的分布情况;对于连续型随机变量,我们通常用 概率密度函数 来表示随机变量取值的分布情况。
- 注意:朴素贝叶斯与贝叶斯估计是不同的概念(李航《统计学习方法》p47最底下注释)



