P3373 【模板】线段树 2
P3373 【模板】线段树 2
相对于线段树模板1有了区间乘的操作，所以增加了一个乘的延迟标记，当加和乘的次序不同的时候，我们要好好考虑这两个延迟标记对孩子的影响。所以这里我们是采取的是先乘后加。
线段树里面也要分清楚是延迟标记依赖就更新自己的值还是把延迟标记传递给孩子的时候才更新自己的值。
题目描述
如题，已知一个数列，你需要进行下面三种操作：
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
输入输出格式
输入格式：
第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数，表示一个操作，具体如下：
操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k
操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k
操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果
输出格式：
输出包含若干行整数，即为所有操作3的结果。
输入输出样例
说明
时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=8，M<=10
对于70%的数据：N<=1000，M<=10000
对于100%的数据：N<=100000，M<=100000
（数据已经过加强^_^）
样例说明：
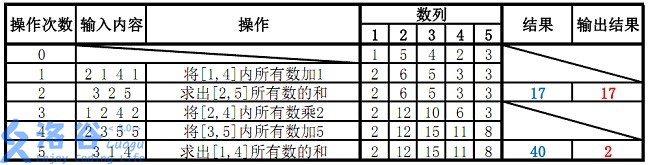
故输出应为17、2（40 mod 38=2）
首先先说明本题的思路。题目要求有三种操作，两种是不同的在线修改，还有一种是在查询取模后的结果。而这两种操作又是区间乘法和区间加法，我们可以惊喜的发现这两种操作对于取模运算来说都是自由的！但是面对非常大的数据，我们必须思考怎么样用线段树优雅的跑过这道题目。
面对这两种操作，可以联想到线段树的一个非常好的功能就是lazytag，只计算出确实需要访问的区间的真实值，其他的保存在lazytag里面，这样可以近似O(NlogN)的运行起来。在尝试着写了只有一个lazetag的程序之后我们发现一个lazytag是不能够解决问题的，那就上两个，分别表示乘法意义上的lazytag和加法意义上的lazytag。紧接着想到pushdown操作之后我们又发现必须在向下传递lazytag的时候人为地为这两个lazytag规定一个先后顺序，排列组合一下只有两种情况：
①加法优先，即规定好segtree[root*2].value=((segtree[root*2].value+segtree[root].add)*segtree[root].mul)%p，问题是这样的话非常不容易进行更新操作，假如改变一下add的数值，mul也要联动变成奇奇怪怪的分数小数损失精度，我们内心是很拒绝的；
②乘法优先，即规定好segtree[root*2].value=(segtree[root*2].value*segtree[root].mul+segtree[root].add*(本区间长度))%p，这样的话假如改变add的数值就只改变add，改变mul的时候把add也对应的乘一下就可以了，没有精度损失，看起来很不错。
讲解的时候举实例就好
比如3-3位置是5
操作 1-5 *2
然后 1-3 +4
然后 1-3 *3
此时位置3-3的值应该为（5*2+4）*3=42
1-5 乘标签2 加标签0
1-3 乘标签2 加标签0
1-5 乘标签0 加标签0
1-3 乘标签2 加标签4
1-3 乘标签6 加标签12
1-3 乘标签6 加标签12
5*6+12
就是父亲在获得标签之后会立马往下传一次，然后自己就没有了，所以能保证标签的顺序
接着贴上详细注释版代码：
1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 //题目中给的p 5 int p; 6 //暂存数列的数组 7 long long a[100007]; 8 //线段树结构体，v表示此时的答案，mul表示乘法意义上的lazytag，add是加法意义上的 9 struct node{ 10 long long v, mul, add; 11 }st[400007]; 12 //buildtree 13 void bt(int root, int l, int r){ 14 //初始化lazytag 15 st[root].mul=1; 16 st[root].add=0; 17 if(l==r){ 18 st[root].v=a[l]; 19 } 20 else{ 21 int m=(l+r)/2; 22 bt(root*2, l, m); 23 bt(root*2+1, m+1, r); 24 st[root].v=st[root*2].v+st[root*2+1].v; 25 } 26 st[root].v%=p; 27 return ; 28 } 29 //核心代码，维护lazytag 30 void pushdown(int root, int l, int r){ 31 int m=(l+r)/2; 32 //根据我们规定的优先度，儿子的值=此刻儿子的值*爸爸的乘法lazytag+儿子的区间长度*爸爸的加法lazytag 33 st[root*2].v=(st[root*2].v*st[root].mul+st[root].add*(m-l+1))%p; 34 st[root*2+1].v=(st[root*2+1].v*st[root].mul+st[root].add*(r-m))%p; 35 //很好维护的lazytag 36 st[root*2].mul=(st[root*2].mul*st[root].mul)%p; 37 st[root*2+1].mul=(st[root*2+1].mul*st[root].mul)%p; 38 st[root*2].add=(st[root*2].add*st[root].mul+st[root].add)%p; 39 st[root*2+1].add=(st[root*2+1].add*st[root].mul+st[root].add)%p; 40 //把父节点的值初始化 41 st[root].mul=1; 42 st[root].add=0; 43 return ; 44 } 45 //update1，乘法，stdl此刻区间的左边，stdr此刻区间的右边，l给出的左边，r给出的右边 46 void ud1(int root, int stdl, int stdr, int l, int r, long long k){ 47 //假如本区间和给出的区间没有交集 48 if(r<stdl || stdr<l){ 49 return ; 50 } 51 //假如给出的区间包含本区间 52 if(l<=stdl && stdr<=r){ 53 st[root].v=(st[root].v*k)%p; 54 st[root].mul=(st[root].mul*k)%p; 55 st[root].add=(st[root].add*k)%p; 56 return ; 57 } 58 //假如给出的区间和本区间有交集，但是也有不交叉的部分 59 //先传递lazytag 60 pushdown(root, stdl, stdr); 61 int m=(stdl+stdr)/2; 62 ud1(root*2, stdl, m, l, r, k); 63 ud1(root*2+1, m+1, stdr, l, r, k); 64 st[root].v=(st[root*2].v+st[root*2+1].v)%p; 65 return ; 66 } 67 //update2，加法，和乘法同理 68 void ud2(int root, int stdl, int stdr, int l, int r, long long k){ 69 if(r<stdl || stdr<l){ 70 return ; 71 } 72 if(l<=stdl && stdr<=r){ 73 st[root].add=(st[root].add+k)%p; 74 st[root].v=(st[root].v+k*(stdr-stdl+1))%p; 75 return ; 76 } 77 pushdown(root, stdl, stdr); 78 int m=(stdl+stdr)/2; 79 ud2(root*2, stdl, m, l, r, k); 80 ud2(root*2+1, m+1, stdr, l, r, k); 81 st[root].v=(st[root*2].v+st[root*2+1].v)%p; 82 return ; 83 } 84 //访问，和update一样 85 long long query(int root, int stdl, int stdr, int l, int r){ 86 if(r<stdl || stdr<l){ 87 return 0; 88 } 89 if(l<=stdl && stdr<=r){ 90 return st[root].v; 91 } 92 pushdown(root, stdl, stdr); 93 int m=(stdl+stdr)/2; 94 return (query(root*2, stdl, m, l, r)+query(root*2+1, m+1, stdr, l, r))%p; 95 } 96 int main(){ 97 int n, m; 98 scanf("%d%d%d", &n, &m, &p); 99 for(int i=1; i<=n; i++){ 100 scanf("%lld", &a[i]); 101 } 102 bt(1, 1, n); 103 while(m--){ 104 int chk; 105 scanf("%d", &chk); 106 int x, y; 107 long long k; 108 if(chk==1){ 109 scanf("%d%d%lld", &x, &y, &k); 110 ud1(1, 1, n, x, y, k); 111 } 112 else if(chk==2){ 113 scanf("%d%d%lld", &x, &y, &k); 114 ud2(1, 1, n, x, y, k); 115 } 116 else{ 117 scanf("%d%d", &x, &y); 118 printf("%lld\n", query(1, 1, n, x, y)); 119 } 120 } 121 return 0; 122 }
