P1364 医院设置
P1364 医院设置
题目描述
设有一棵二叉树,如图:
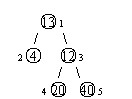
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为l。如上图中,
若医院建在1 处,则距离和=4+12+2*20+2*40=136;若医院建在3 处,则距离和=4*2+13+20+40=81……
输入输出格式
输入格式:
第一行一个整数n,表示树的结点数。(n≤100)
接下来的n行每行描述了一个结点的状况,包含三个整数,整数之间用空格(一个或多个)分隔,其中:第一个数为居民人口数;第二个数为左链接,为0表示无链接;第三个数为右链接。
输出格式:
一个整数,表示最小距离和。
输入输出样例
输入样例#1:
5 13 2 3 4 0 0 12 4 5 20 0 0 40 0 0
输出样例#1:
81
分析和解答:
1、暴力
医院建的位置就是root点
数据结构是一个双向图
代价=步长*人数
时间复杂度:O(n*n)

1 #include <bits/stdc++.h> 2 const int N=1e2+10; 3 const int INFINITE=1<<30; 4 using namespace std; 5 vector<int> vct[N]; 6 int val[N],n,ans=INFINITE; 7 bool vis[N]; 8 9 void init(){ 10 cin>>n; 11 int w,l,r; 12 for(int i=1;i<=n;i++){ 13 cin>>w>>l>>r; 14 val[i]=w; 15 if(l){ 16 vct[i].push_back(l); 17 vct[l].push_back(i); 18 } 19 if(r){ 20 vct[i].push_back(r); 21 vct[r].push_back(i); 22 } 23 } 24 } 25 26 int find(int r,int step){ 27 if(vis[r]) return 0; 28 vis[r]=true; 29 int ans=val[r]*step; 30 for(int i=0;i<vct[r].size();i++){ 31 int v=vct[r][i]; 32 ans+=find(v,step+1); 33 } 34 return ans; 35 } 36 37 void search(){ 38 for(int i=1;i<=n;i++){ 39 memset(vis,false,sizeof(vis)); 40 int tmp=find(i,0); 41 if(tmp<ans) ans=tmp; 42 } 43 } 44 45 46 int main(){ 47 //freopen("in.txt","r",stdin); 48 init(); 49 search(); 50 cout<<ans<<endl; 51 return 0; 52 }
2、最短路解法
spfa解法
求出医院的那个点到其它点的距离
时间复杂度:O(n*2e+n*n) e大概等于2n

只列出了最短路里面的一种解法,当然也可以用其它最短路来做
1 #include <bits/stdc++.h> 2 const int N=1e2+10; 3 const int INFINITE=1<<30; 4 using namespace std; 5 vector<int> vct[N]; 6 int val[N],n,ans=INFINITE,dis[N]; 7 bool vis[N]; 8 queue<int> q; 9 10 void init(){ 11 cin>>n; 12 int w,l,r; 13 for(int i=1;i<=n;i++){ 14 cin>>w>>l>>r; 15 val[i]=w; 16 if(l){ 17 vct[i].push_back(l); 18 vct[l].push_back(i); 19 } 20 if(r){ 21 vct[i].push_back(r); 22 vct[r].push_back(i); 23 } 24 } 25 } 26 27 void spfa(int s){ 28 dis[s]=0; 29 q.push(s); 30 vis[s]=true; 31 while(!q.empty()){ 32 int u=q.front();q.pop(); 33 vis[u]=false; 34 for(int i=0;i<vct[u].size();i++){ 35 int v=vct[u][i]; 36 if(dis[v]>dis[u]+1){ 37 dis[v]=dis[u]+1; 38 if(!vis[v]){ 39 q.push(v); 40 vis[v]=true; 41 } 42 } 43 } 44 } 45 } 46 47 void search(){ 48 for(int i=1;i<=n;i++){ 49 memset(vis,false,sizeof(vis)); 50 memset(dis,0x3f,sizeof(dis)); 51 spfa(i); 52 int tmp=0; 53 for(int i=1;i<=n;i++){ 54 tmp+=dis[i]*val[i]; 55 } 56 if(tmp<ans) ans=tmp; 57 } 58 } 59 60 61 int main(){ 62 //freopen("in.txt","r",stdin); 63 init(); 64 search(); 65 cout<<ans<<endl; 66 return 0; 67 }
3、树形dp解法
dp[i]表示以i为根的子树的最优值。
v是i的孩子
dp[i] =dp[v]+i的孩子和
时间复杂度:O(n*n)

1 #include <bits/stdc++.h> 2 const int N=1e2+10; 3 const int INFINITE=1<<30; 4 using namespace std; 5 vector<int> vct[N]; 6 int val[N],n,ans=INFINITE,dp[N]; 7 bool vis[N]; 8 9 void init(){ 10 cin>>n; 11 int w,l,r; 12 for(int i=1;i<=n;i++){ 13 cin>>w>>l>>r; 14 val[i]=w; 15 if(l){ 16 vct[i].push_back(l); 17 vct[l].push_back(i); 18 } 19 if(r){ 20 vct[i].push_back(r); 21 vct[r].push_back(i); 22 } 23 } 24 } 25 26 int dfs(int r){ 27 if(vis[r]) return 0; 28 vis[r]=true; 29 int sum=0; 30 for(int i=0;i<vct[r].size();i++){ 31 int v=vct[r][i]; 32 if(!vis[v]){ 33 sum+=(val[v]+dfs(v)); 34 dp[r]+=dp[v]; 35 } 36 } 37 dp[r]+=sum; 38 return sum; 39 } 40 41 void search(){ 42 for(int i=1;i<=n;i++){ 43 memset(vis,false,sizeof(vis)); 44 memset(dp,0,sizeof(dp)); 45 dfs(i); 46 if(dp[i]<ans) ans=dp[i]; 47 } 48 } 49 50 51 int main(){ 52 //freopen("in.txt","r",stdin); 53 init(); 54 search(); 55 cout<<ans<<endl; 56 return 0; 57 }



