单调队列
单调队列
单调队列和单调栈两者功能相同,只是维护的时候不同。
我们从最简单的问题开始:
给定一个长度为N的整数数列a(i),i=0,1,...,N-1和窗长度k.
要求:
f(i) = max{a(i-k+1),a(i-k+2),..., a(i)},i = 0,1,...,N-1
问题的另一种描述就是用一个长度为k的窗在整数数列上移动,求窗里面所包含的数的最大值。
解法一:
很直观的一种解法,那就是从数列的开头,将窗放上去,然后找到这最开始的k个数的最大值,然后窗最后移一个单元,继续找到k个数中的最大值。
这种方法每求一个f(i),都要进行k-1次的比较,复杂度为O(N*k)。
那么有没有更快一点的算法呢?
解法二:
我们知道,上一种算法有一个地方是重复比较了,就是在找当前的f(i)的时候,i的前面k-1个数其它在算f(i-1)的时候我们就比较过了。那么我们能不能保存上一次的结果呢?当然主要是i的前k-1个数中的最大值了。答案是可以,这就要用到单调递减队列。
单调递减队列是这么一个队列,它的头元素一直是队列当中的最大值,而且队列中的值是按照递减的顺序排列的。我们可以从队列的末尾插入一个元素,可以从队列的两端删除元素。
1.首先看插入元素:为了保证队列的递减性,我们在插入元素v的时候,要将队尾的元素和v比较,如果队尾的元素不大于v,则删除队尾的元素,然后继续将新的队尾的元素与v比较,直到队尾的元素大于v,这个时候我们才将v插入到队尾。
2.队尾的删除刚刚已经说了,那么队首的元素什么时候删除呢?由于我们只需要保存i的前k-1个元素中的最大值,所以当队首的元素的索引或下标小于i-k+1的时候,就说明队首的元素对于求f(i)已经没有意义了,因为它已经不在窗里面了。所以当index[队首元素]<i-k+1时,将队首元素删除。
从上面的介绍当中,我们知道,单调队列与队列唯一的不同就在于它不仅要保存元素的值,而且要保存元素的索引(当然在实际应用中我们可以只需要保存索引,而通过索引间接找到当前索引的值)。
为了让读者更明白一点,我举个简单的例子。
假设数列为:8,7,12,5,16,9,17,2,4,6.N=10,k=3.
那么我们构造一个长度为3的单调递减队列:
首先,那8和它的索引0放入队列中,我们用(8,0)表示,每一步插入元素时队列中的元素如下:
0:插入8,队列为:(8,0)
1:插入7,队列为:(8,0),(7,1)
2:插入12,队列为:(12,2)
3:插入5,队列为:(12,2),(5,3)
4:插入16,队列为:(16,4)
5:插入9,队列为:(16,4),(9,5)
。。。。依此类推
那么f(i)就是第i步时队列当中的首元素:8,8,12,12,16,16,。。。
1 #include<iostream> 2 #include<queue> 3 4 using namespace std; 5 6 struct Node 7 { 8 int val; 9 int index; 10 }; 11 12 //数组序列 13 void GetMax(int *numSequence,int len, int *result,int k) 14 { 15 Node *que = new Node[len]; 16 //头尾指针 17 int head = 0; 18 int end = 0; 19 20 for(int i=0;i<len;i++) 21 { 22 Node tmp; 23 //填节点 24 tmp.val = numSequence[i]; 25 tmp.index = i; 26 27 //要插入的数大的情况 28 while(end!=0 && que[end].val<=numSequence[i]) 29 --end; 30 //要插入的数小于队尾元素 31 ++end; 32 que[end] = tmp; 33 34 //找ans 35 while(end!=0 && que[head].index<i-k+1) 36 ++head; 37 result[i] = que[head].val; 38 } 39 delete []que; 40 } 41 42 int main() 43 { 44 int len, k; 45 cin>>len>>k; 46 47 int *numSequence = new int[len]; 48 int *maxResult = new int[len]; 49 50 for(int i=0;i<len;i++) 51 cin>>numSequence[i]; 52 53 GetMax(numSequence,len,maxResult,k); 54 55 for(int i=k-1;i<len;i++) 56 cout<<i<<": "<<maxResult[i]<<endl; 57 58 delete[]numSequence; 59 delete[]maxResult; 60 numSequence = NULL; 61 maxResult = NULL; 62 63 return 0; 64 }
根据实例来敲代码,变量之间的关系很好 掌握
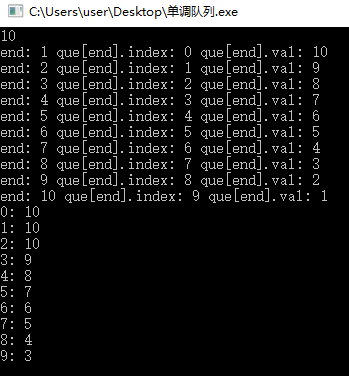
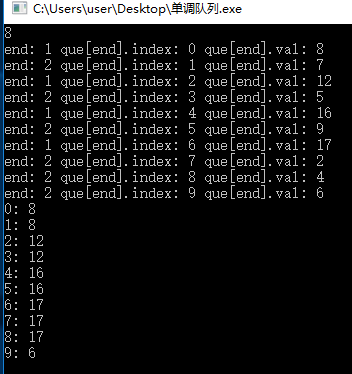
输入数据:
10 3
10 9 8 7 6 5 4 3 2 1
10 3
8 7 12 5 16 9 17 2 4 6
1 #include<iostream> 2 #include<queue> 3 4 using namespace std; 5 6 struct Node 7 { 8 int val; 9 int index; 10 }; 11 12 //数组序列 13 void GetMax(int *numSequence,int len, int *result,int k) 14 { 15 Node *que = new Node[len]; 16 //头尾指针 17 int head = 0; 18 int end = 0; 19 20 for(int i=0;i<len;i++) 21 { 22 Node tmp; 23 //填节点 24 tmp.val = numSequence[i]; 25 tmp.index = i; 26 27 //要插入的数大的情况 28 while(end!=0 && que[end].val<=numSequence[i]) 29 --end; 30 //要插入的数小于队尾元素 31 ++end; 32 que[end] = tmp; 33 cout<<"end: "<<end<<" que[end].index: "<<que[end].index<<" que[end].val: "<<que[end].val<<endl; 34 //找ans 35 //如果里面还有元素 end!=0 36 //并且 37 if(i<k) result[i]=que[head+1].val; 38 else{ 39 int index=que[head+1].index; 40 int indexNow=que[end].index; 41 //队头的元素如果和当前元素的距离只差大于3了 42 while(indexNow-index>=3) head++,index=que[head+1].index;; 43 } 44 result[i]=que[head+1].val; 45 46 } 47 delete []que; 48 } 49 50 51 52 //直接根据实例来写代码,这样下标不容易弄混 53 //取得实例 10 3 {10,9,8.。。1} 54 //取得实例 10 3 {10,1,2,3,9,8,。。。} 55 int main() 56 { 57 freopen("in.txt","r",stdin); 58 //freopen("in2.txt","r",stdin); 59 int len, k; 60 cin>>len>>k; 61 62 //数组 63 int *numSequence = new int[len]; 64 //窗的终点 位置 65 int *maxResult = new int[len]; 66 67 for(int i=0;i<len;i++) 68 cin>>numSequence[i]; 69 70 cout<<numSequence[0]<<endl; 71 72 GetMax(numSequence,len,maxResult,k); 73 74 for(int i=0;i<len;i++) 75 cout<<i<<": "<<maxResult[i]<<endl; 76 77 delete[]numSequence; 78 delete[]maxResult; 79 numSequence = NULL; 80 maxResult = NULL; 81 82 return 0; 83 }
写完代码反复检查然后再提交,这样会省掉超级多的检查时间。
1 #include <bits/stdc++.h> 2 using namespace std; 3 struct node{ 4 int index; 5 int val; 6 }; 7 int n,k; 8 void getMax(int *a,int *ans,int n,int k){ 9 node *q=new node[100]; 10 int h=0,r=0; 11 for(int i=1;i<=n;i++){ 12 node tmp;tmp.val=a[i];tmp.index=i; 13 while(h<r&&q[r-1].val<=tmp.val) r--; 14 q[r++]=tmp; 15 if(i<=k) ans[i]=q[h].val; 16 else while(q[r-1].index-q[h].index>=k) h++; 17 ans[i]=q[h].val; 18 } 19 delete[] q; 20 } 21 22 23 int main(){ 24 freopen("in.txt","r",stdin); 25 int *a=new int[100]; 26 int *ans=new int[100]; 27 cin>>n>>k; 28 for(int i=1;i<=n;i++) cin>>a[i]; 29 getMax(a,ans,n,k); 30 for(int i=1;i<=n;i++) cout<<ans[i]<<" ";cout<<endl; 31 delete[] a; 32 delete[] ans; 33 a=NULL; 34 ans=NULL; 35 return 0; 36 }

数组传引用
#include <bits/stdc++.h> using namespace std; struct node{ int index; int val; }; int n,k; void getMax(int (&a)[100],int (&ans)[100],int n,int k){ node q[100]; int h=0,r=0; for(int i=1;i<=n;i++){ node tmp;tmp.val=a[i];tmp.index=i; while(h<r&&q[r-1].val<=tmp.val) r--; q[r++]=tmp; if(i<=k) ans[i]=q[h].val; else while(q[r-1].index-q[h].index>=k) h++; ans[i]=q[h].val; } } int main(){ freopen("in.txt","r",stdin); int a[100],ans[100]; cin>>n>>k; for(int i=1;i<=n;i++) cin>>a[i]; getMax(a,ans,n,k); for(int i=1;i<=n;i++) cout<<ans[i]<<" ";cout<<endl; return 0; }



