微信扫一扫打赏支持

深入理解dijkstra+堆优化

深入理解dijkstra+堆优化

其实就这几种代码几种结构，记住了完全就可以举一反三，所以多记多练多优化多思考。

Dijkstra
 
      对于一个有向图或无向图，所有边权为正（边用邻接矩阵的形式给出），给定a和b，求a到b的最短路，保证a一定能够到达b。这条最短路是否一定存在呢？答案是肯定的。相反，最长路就不一定了，由于边权为正，如果遇到有环的时候，可以一直在这个环上走，因为要找最长的，这样就使得路径越变越长，永无止境，所以对于正权图，在可达的情况下最短路一定存在，最长路则不一定存在。这里先讨论正权图的最短路问题。
      最短路满足最优子结构性质，所以是一个动态规划问题。最短路的最优子结构可以描述为：
      D(s, t) = {Vs ... Vi ... Vj ... Vt}表示s到t的最短路，其中i和j是这条路径上的两个中间结点，那么D(i, j)必定是i到j的最短路，这个性质是显然的，可以用反证法证明。
      基于上面的最优子结构性质，如果存在这样一条最短路D(s, t) = {Vs ... Vi Vt}，其中i和t是最短路上相邻的点，那么D(s, i) = {Vs ... Vi} 必定是s到i的最短路。Dijkstra算法就是基于这样一个性质，通过最短路径长度递增，逐渐生成最短路。
      Dijkstra算法是最经典的最短路算法，用于计算正权图的单源最短路（Single Source Shortest Path，源点给定，通过该算法可以求出起点到所有点的最短路），它是基于这样一个事实：如果源点到x点的最短路已经求出，并且保存在d[x] ( 可以将它理解为D(s, x) )上，那么可以利用x去更新 x能够直接到达的点 的最短路。即：
      d[y] = min{ d[y], d[x] + w(x, y) }           y为x能够直接到达的点，w(x, y) 则表示x->y这条有向边的边权
      具体算法描述如下：对于图G = <V, E>，源点为s，d[i]表示s到i的最短路，visit[i]表示d[i]是否已经确定(布尔值)。
      1) 初始化 所有顶点 d[i] = INF, visit[i] = false，令d[s] = 0；
      2) 从所有visit[i]为false的顶点中找到一个d[i]值最小的，令x = i; 如果找不到，算法结束；
      3) 标记visit[x] = true, 更新和x直接相邻的所有顶点y的最短路： d[y] = min{ d[y], d[x] + w(x, y) }
     （第三步中如果y和x并不是直接相邻，则令w(x, y) = INF）
 
实例：

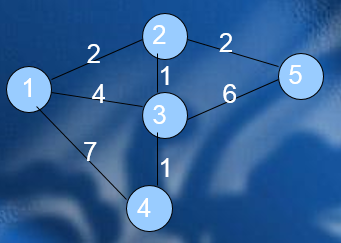
输入：

5 7
1 2 2
2 5 2
1 3 4
1 4 7
3 4 1
2 3 1
3 5 6

 

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 int n,m;
 4 struct node{
 5     int to;
 6     int w;
 7 };
 8 int edgeNum[100];
 9 vector<node> vec[100];
10 int dis[100];
11 bool vis[100];
12 
13 void addEdge(int a,int b,int w){
14     edgeNum[a]++;
15     node *p=new node();
16     p->to=b;
17     p->w=w;
18     vec[a].push_back(*p); 
19 }
20 
21 void init(){
22     cin>>n>>m;
23     for(int i=1;i<=m;i++){
24         int a,b,w;
25         cin>>a>>b>>w;
26         addEdge(a,b,w);
27         addEdge(b,a,w);
28     }
29 }
30 
31 void dijkstra(int start){
32     memset(dis,0x3f,sizeof(dis));
33     dis[start]=0;
34     for(int i=0;i<edgeNum[start];i++) {
35         int b=vec[start][i].to;
36         int w=vec[start][i].w;
37         dis[b]=w;
38     }
39     vis[start]=1;
40     for(int k=1;k<=n-1;k++){
41         int minV=0x7fffffff,min_i;
42         for(int i=1;i<=n;i++){
43             if(!vis[i]&&dis[i]<minV){
44                 minV=dis[i];
45                 min_i=i;
46             }
47         }
48         vis[min_i]=true;
49         for(int i=0;i<edgeNum[min_i];i++){
50             int b=vec[min_i][i].to;
51             int w=vec[min_i][i].w;
52             if(!vis[b]&&dis[b]>dis[min_i]+w){
53                 dis[b]=dis[min_i]+w;
54             } 
55         } 
56         
57     }
58     
59     
60     
61 }
62 
63 void print(){
64     for(int i=1;i<=n;i++)
65         cout<<dis[i]<<" ";
66     cout<<endl;    
67 }
68 
69 int main(){
70     freopen("in.txt","r",stdin);
71     init();
72     dijkstra(2);
73     print();
74     return 0;
75 }

上面的代码说几点：

1、13行到19行的代码可以通过给结构体添加构造函数来优化。

2、dijkstra中的节点如果改成u，v的话更清晰

3、朴素的dijkstra分为如下几步：初始化dis数组，n-1轮（找最优节点，更新）

求节点1到其它节点的距离：

 

堆优化：

  1 #include <bits/stdc++.h>
  2 using namespace std;
  3 int n,m;
  4 struct node{
  5     int to;
  6     int w;
  7 };
  8 int edgeNum[100];
  9 vector<node> vec[100];
 10 int dis[100];
 11 bool vis[100];
 12 
 13 void addEdge(int a,int b,int w){
 14     edgeNum[a]++;
 15     node *p=new node();
 16     p->to=b;
 17     p->w=w;
 18     vec[a].push_back(*p); 
 19 }
 20 
 21 void init(){
 22     cin>>n>>m;
 23     for(int i=1;i<=m;i++){
 24         int a,b,w;
 25         cin>>a>>b>>w;
 26         addEdge(a,b,w);
 27         addEdge(b,a,w);
 28     }
 29 }
 30 
 31 void dijkstra(int start){
 32     memset(dis,0x3f,sizeof(dis));
 33     dis[start]=0;
 34     for(int i=0;i<edgeNum[start];i++) {
 35         int b=vec[start][i].to;
 36         int w=vec[start][i].w;
 37         dis[b]=w;
 38     }
 39     vis[start]=1;
 40     for(int k=1;k<=n-1;k++){
 41         int minV=0x7fffffff,min_i;
 42         for(int i=1;i<=n;i++){
 43             if(!vis[i]&&dis[i]<minV){
 44                 minV=dis[i];
 45                 min_i=i;
 46             }
 47         }
 48         vis[min_i]=true;
 49         for(int i=0;i<edgeNum[min_i];i++){
 50             int b=vec[min_i][i].to;
 51             int w=vec[min_i][i].w;
 52             if(!vis[b]&&dis[b]>dis[min_i]+w){
 53                 dis[b]=dis[min_i]+w;
 54             } 
 55         } 
 56         
 57     }    
 58 }
 59 
 60 
 61 //dijkstra的堆优化
 62 struct qnode{
 63     int i_i;
 64     int dis_i;
 65     qnode(int i,int dis_i){
 66         this->i_i=i;
 67         this->dis_i=dis_i;
 68     }
 69 }; 
 70 struct myCmp{
 71     bool operator ()(const qnode &p1,const qnode &p2){
 72         return p1.dis_i>p2.dis_i;
 73     }
 74 };
 75 priority_queue<qnode,vector<qnode>,myCmp> q;
 76 void dijkstra_2(int start){
 77     memset(dis,0x3f,sizeof(dis));//和SPFA一样，这里最开始全都是无穷大 
 78     dis[start]=0;
 79     q.push(qnode(start,dis[start]));
 80     while(!q.empty()){
 81         qnode p=q.top();
 82         q.pop();
 83         int min_i= p.i_i;
 84         int minV=p.dis_i;
 85         if(vis[min_i]) continue;
 86         vis[min_i]=true;
 87         for(int i=0;i<edgeNum[min_i];i++){
 88             int b=vec[min_i][i].to;
 89             int w=vec[min_i][i].w;
 90             if(!vis[b]&&dis[b]>dis[min_i]+w){
 91                 dis[b]=dis[min_i]+w;
 92                 q.push(qnode(b,dis[b]));
 93             }
 94         }
 95         
 96     }
 97 } 
 98 
 99 void print(){
100     for(int i=1;i<=n;i++)
101         cout<<dis[i]<<" ";
102     cout<<endl;    
103 }
104 
105 int main(){
106     freopen("in.txt","r",stdin);
107     init();
108     //dijkstra(2);
109     dijkstra_2(1);
110     print();
111     return 0;
112 }

关于上面的代码说几点：

1、堆优化的话priority_queue得非常熟悉

2、这里堆优化的时候使用了结构体，里面的成员是i和dis[i]，其实这个dis[i]可以直接写在外面，但是比较规则还是得自己定义

3、用队列做的所有的题核心代码一定是while(!queue.empty()){}

4、还是要多写多练，要熟悉，基础打好

5、和SPFA一样，如果点更新成功就加进队列

求节点1到其它节点的距离：

 

堆优化2

  1 #include <bits/stdc++.h>
  2 using namespace std;
  3 int n,m;
  4 struct node{
  5     int to;
  6     int w;
  7 };
  8 int edgeNum[100];
  9 vector<node> vec[100];
 10 int dis[100];
 11 bool vis[100];
 12 
 13 void addEdge(int a,int b,int w){
 14     edgeNum[a]++;
 15     node *p=new node();
 16     p->to=b;
 17     p->w=w;
 18     vec[a].push_back(*p); 
 19 }
 20 
 21 void init(){
 22     cin>>n>>m;
 23     for(int i=1;i<=m;i++){
 24         int a,b,w;
 25         cin>>a>>b>>w;
 26         addEdge(a,b,w);
 27         addEdge(b,a,w);
 28     }
 29 }
 30 
 31 void dijkstra(int start){
 32     memset(dis,0x3f,sizeof(dis));
 33     dis[start]=0;
 34     for(int i=0;i<edgeNum[start];i++) {
 35         int b=vec[start][i].to;
 36         int w=vec[start][i].w;
 37         dis[b]=w;
 38     }
 39     vis[start]=1;
 40     for(int k=1;k<=n-1;k++){
 41         int minV=0x7fffffff,min_i;
 42         for(int i=1;i<=n;i++){
 43             if(!vis[i]&&dis[i]<minV){
 44                 minV=dis[i];
 45                 min_i=i;
 46             }
 47         }
 48         vis[min_i]=true;
 49         for(int i=0;i<edgeNum[min_i];i++){
 50             int b=vec[min_i][i].to;
 51             int w=vec[min_i][i].w;
 52             if(!vis[b]&&dis[b]>dis[min_i]+w){
 53                 dis[b]=dis[min_i]+w;
 54             } 
 55         } 
 56         
 57     }    
 58 }
 59 
 60 
 61 //dijkstra的堆优化
 62 struct myCmp{
 63     bool operator ()(int a,int b){
 64         return dis[a]>dis[b];
 65     }
 66 };
 67 priority_queue<int,vector<int>,myCmp> q;
 68 void dijkstra_2(int start){
 69     memset(dis,0x3f,sizeof(dis));//和SPFA一样，这里最开始全都是无穷大 
 70     dis[start]=0;
 71     q.push(start);
 72     while(!q.empty()){
 73         int u=q.top();
 74         q.pop();
 75         if(vis[u]) continue;
 76         vis[u]=true;
 77         for(int i=0;i<edgeNum[u];i++){
 78             int b=vec[u][i].to;
 79             int w=vec[u][i].w;
 80             if(!vis[b]&&dis[b]>dis[u]+w){
 81                 dis[b]=dis[u]+w;
 82                 q.push(b);
 83             }
 84         }
 85         
 86     }
 87 } 
 88 
 89 void print(){
 90     for(int i=1;i<=n;i++)
 91         cout<<dis[i]<<" ";
 92     cout<<endl;    
 93 }
 94 
 95 int main(){
 96     freopen("in.txt","r",stdin);
 97     init();
 98     //dijkstra(2);
 99     dijkstra_2(1);
100     print();
101     return 0;
102 }
堆优化2

关于上面的代码说几点：

1、dijkstra的优先队列优化写法和spfa非常像，只不过spfa多加了一个是否在队列里面的标志

2、这里储存图用的是vector数组

3、优先队列里面的元素是int，然而我们还是重写了优先队列的比较函数，因为队列里面是节点编号，但是我们要比较的是dis[i]

4、和SPFA一样，dis[i]最开始全都是无穷大 ,并且最开始只更新dis[start]=0

求节点1到其它节点的距离：

 

 

其它代码：

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int n,m,S,tot,Next[500010],head[20000],tree[500010],val[500010];
bool visit[20000];
long long dis[20000];
struct cmp
{
    bool operator()(int a,int b)
    {
        return dis[a]>dis[b];
    }
};
priority_queue<int,vector<int>,cmp> Q;
void add(int x,int y,int z)
{
    tot++;
    Next[tot]=head[x];
    head[x]=tot;
    tree[tot]=y;
    val[tot]=z;
}
int main()
{
    scanf("%d%d%d",&n,&m,&S);
    tot=0;
    for (int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        if (x==y) continue;
        add(x,y,z);
    }
    for (int i=1;i<=n;i++) 
    {
        visit[i]=false;
        dis[i]=2147483647;
    }
    Q.push(S);
    dis[S]=0;
    while (!Q.empty())
    {
        int u=Q.top();
        Q.pop();
        if (visit[u]) continue;
        visit[u]=true;
        for (int i=head[u];i;i=Next[i])
        {
            int v=tree[i];
            if (!visit[v]&&dis[v]>dis[u]+(long long)val[i])
            {   
                dis[v]=dis[u]+val[i];
                Q.push(v);
            }
        }
    }
    for (int i=1;i<=n-1;i++) printf("%lld ",dis[i]);
    printf("%lld\n",dis[n]);
    return 0;
}

 

vector数组版

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 struct node{
 4     int v;
 5     int w;
 6     node(int v,int w){
 7         this->v=v;
 8         this->w=w;
 9     }
10 };
11 vector<node> vec[100];
12 int edgeNum[100];
13 int n,m;
14 int dis[100];
15 bool vis[100];
16 
17 void addEdge(int u,int v,int w){
18     edgeNum[u]++;
19     vec[u].push_back(node(v,w));
20 }
21 
22 void init(){
23     cin>>n>>m;
24     for(int i=1;i<=m;i++){
25         int u,v,w;
26         cin>>u>>v>>w;
27         addEdge(u,v,w);
28         addEdge(v,u,w);
29     }
30 }
31 
32 struct myCmp{
33     bool operator ()(const int &u,const int &v){
34         return dis[u]>dis[v];
35     }
36 };
37 priority_queue<int,vector<int>,myCmp> q;
38 void dijkstra(int start){
39     memset(dis,0x3f,sizeof(dis));
40     q.push(start);
41     dis[start]=0;
42     while(!q.empty()){
43         int u=q.top();
44         q.pop();
45         if(vis[u]) continue;
46         vis[u]=true;
47         for(int i=0;i<edgeNum[u];i++){
48             int v=vec[u][i].v;
49             int w=vec[u][i].w;
50             if(!vis[v]&&dis[v]>dis[u]+w){
51                 dis[v]=dis[u]+w;
52                 q.push(v);
53             }
54         }
55     }
56 }
57 
58 void print(){
59     for(int i=1;i<=n;i++){
60         cout<<dis[i]<<" ";
61     }
62     cout<<endl;
63 }
64  
65 int main(){
66     freopen("in.txt","r",stdin); 
67     init();
68     dijkstra(2);
69     print();
70     return 0;
71 }

 

posted @ 2017-09-12 00:51  范仁义  阅读(12987)  评论(0)  编辑  收藏  举报