微信扫一扫打赏支持

线段树2 求区间最小值

线段树2 求区间最小值

 

递归，DFS，尤其是二叉树，我只要知道我的返回节点就好，因为DFS的顺序一定是一样的，不同的题目和数据范围也是一样的，只是返回节点让DFS的深度不同。

递归的内容只有两部分：1、不停的递归查找      2、到了叶子节点我返回

所以写递归的时候明确这两块就好。

只是这里在DFS里面还多了一个后序遍历。

 

从数组arr[0...n-1]中查找某个数组某个区间内的最小值，其中数组大小固定，但是数组中的元素的值可以随时更新。

数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树（背景为白色表示叶子节点，非叶子节点的值是其对应数组区间内的最小值，例如根节点表示数组区间arr[0...5]内的最小值是1）：

 

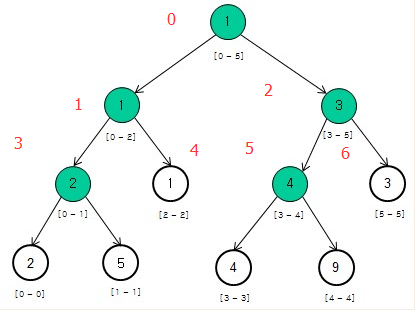
线段树的四种操作：

1、线段树的创建

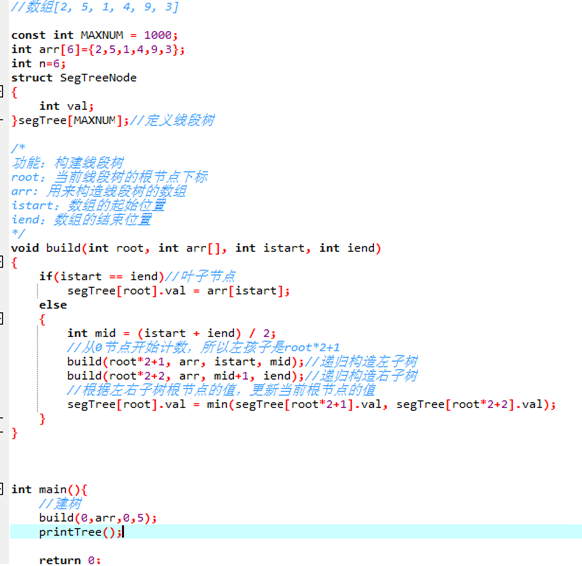
代码是后序遍历，也就是访问完了两个孩子再来访问自己。

DFS就是那样一条路走到底的方式。

DFS的终止条件就是叶子节点。

 

2、线段树的查询

 

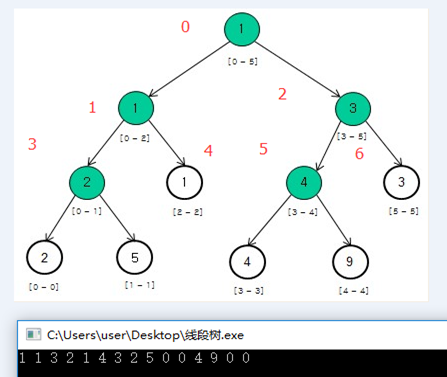
1、当前找的区间小于我们查询区间的话，肯定是查询区间之前被分了，因为我最开始的查询区间是0-5，所以我并不用担心这个时候返回了,

 　　而且被分出去的另外一边肯定会给你返回一个值让你来取两者之间的最小值的。

2、其实还是后序遍历。

3、后序遍历肯定就是用子节点去更新父节点。

4、所以找到最后肯定要去更新0-5区间的值，也就是根节点的值，然后将0-5区间的值返回给查询区间0-3，所以真的完全不用担心当前区间小于查找区间的情况。

5、思想：就是0-3区间能找到的值就返回最小值，其它区间例如4-5就返回INFINITE.

6、思想懂了，理解透彻了，代码还不好写么

 

 

3、线段树的更新单节点

 

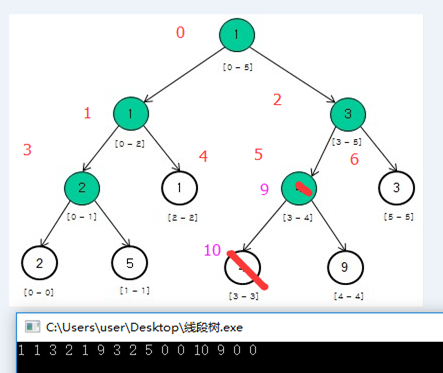
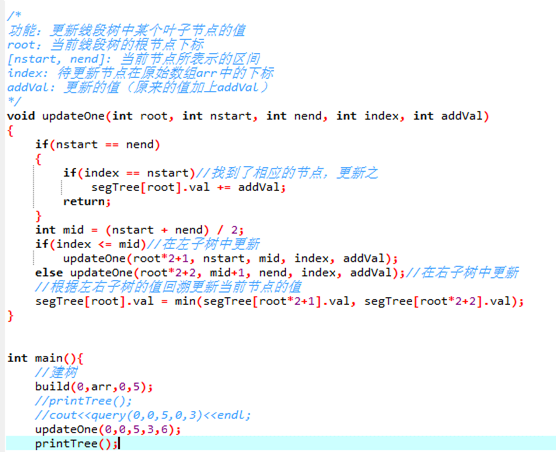
1、找到那个点，并且从那个点开始后序遍历更新父亲节点

2、因为是DFS的终点，肯定就是DFS的终止条件

 

 

4、线段树的更新区间

 

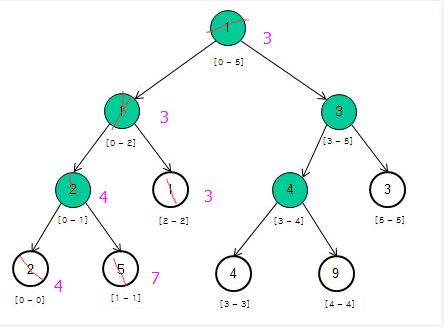
 直接上完整代码吧

  1 #include <bits/stdc++.h>
  2 #define INFINITE 0x3fffffff
  3 using namespace std;
  4 void printTree();
  5 //数组[2, 5, 1, 4, 9, 3]
  6 
  7 const int MAXNUM = 1000;
  8 int arr[6]={2,5,1,4,9,3}; 
  9 int n=6;
 10 struct SegTreeNode
 11 {
 12     int val;
 13     int addMark; 
 14 }segTree[MAXNUM];//定义线段树
 15 
 16 /*
 17 功能：当前节点的标志域向孩子节点传递
 18 root: 当前线段树的根节点下标
 19 */
 20 void pushDown(int root)
 21 {
 22     if(segTree[root].addMark != 0)
 23     {
 24         //设置左右孩子节点的标志域，因为孩子节点可能被多次延迟标记又没有向下传递
 25         //所以是 “+=”
 26         segTree[root*2+1].addMark += segTree[root].addMark;
 27         segTree[root*2+2].addMark += segTree[root].addMark;
 28         //根据标志域设置孩子节点的值。因为我们是求区间最小值，因此当区间内每个元
 29         //素加上一个值时，区间的最小值也加上这个值
 30         segTree[root*2+1].val += segTree[root].addMark;
 31         segTree[root*2+2].val += segTree[root].addMark;
 32         //传递后，当前节点标记域清空
 33         segTree[root].addMark = 0;
 34     }
 35 }
 36 
 37 
 38 /*
 39 功能：构建线段树
 40 root：当前线段树的根节点下标
 41 arr: 用来构造线段树的数组
 42 istart：数组的起始位置
 43 iend：数组的结束位置
 44 */
 45 void build(int root, int arr[], int istart, int iend)
 46 {
 47     segTree[root].addMark = 0;//----设置标延迟记域
 48     if(istart == iend)//叶子节点
 49         segTree[root].val = arr[istart];
 50     else
 51     {
 52         int mid = (istart + iend) / 2;
 53         //从0节点开始计数，所以左孩子是root*2+1 
 54         build(root*2+1, arr, istart, mid);//递归构造左子树
 55         build(root*2+2, arr, mid+1, iend);//递归构造右子树
 56         //根据左右子树根节点的值，更新当前根节点的值
 57         segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val);
 58     }
 59 }
 60 
 61 
 62 /*
 63 功能：线段树的区间查询
 64 root：当前线段树的根节点下标
 65 [nstart, nend]: 当前节点所表示的区间
 66 [qstart, qend]: 此次查询的区间
 67 */
 68 int query(int root, int nstart, int nend, int qstart, int qend)
 69 {
 70     //查询区间和当前节点区间没有交集
 71     if(qstart > nend || qend < nstart)
 72         return INFINITE;
 73     //当前节点区间包含在查询区间内
 74     if(qstart <= nstart && qend >= nend)
 75         return segTree[root].val;
 76     //分别从左右子树查询，返回两者查询结果的较小值
 77     pushDown(root); //延迟标记向下传递
 78     int mid = (nstart + nend) / 2;
 79     return min(query(root*2+1, nstart, mid, qstart, qend),
 80                query(root*2+2, mid + 1, nend, qstart, qend));
 81 
 82 }
 83 
 84 
 85 /*
 86 功能：更新线段树中某个叶子节点的值
 87 root：当前线段树的根节点下标
 88 [nstart, nend]: 当前节点所表示的区间
 89 index: 待更新节点在原始数组arr中的下标
 90 addVal: 更新的值（原来的值加上addVal）
 91 */
 92 void updateOne(int root, int nstart, int nend, int index, int addVal)
 93 {
 94     if(nstart == nend)
 95     {
 96         if(index == nstart)//找到了相应的节点，更新之
 97             segTree[root].val += addVal;
 98         return;
 99     }
100     int mid = (nstart + nend) / 2;
101     if(index <= mid)//在左子树中更新
102         updateOne(root*2+1, nstart, mid, index, addVal);
103     else updateOne(root*2+2, mid+1, nend, index, addVal);//在右子树中更新
104     //根据左右子树的值回溯更新当前节点的值
105     segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val);
106 }
107 
108 
109 
110 /*
111 功能：更新线段树中某个区间内叶子节点的值
112 root：当前线段树的根节点下标
113 [nstart, nend]: 当前节点所表示的区间
114 [ustart, uend]: 待更新的区间
115 addVal: 更新的值（原来的值加上addVal）
116 */
117 void update(int root, int nstart, int nend, int ustart, int uend, int addVal)
118 {
119     //更新区间和当前节点区间没有交集
120     if(ustart > nend || uend < nstart)
121         return ;
122     //当前节点区间包含在更新区间内
123     if(ustart <= nstart && uend >= nend)
124     {
125         segTree[root].addMark += addVal;
126         segTree[root].val += addVal;
127         return ;
128     }
129     pushDown(root); //延迟标记向下传递
130     //更新左右孩子节点
131     int mid = (nstart + nend) / 2;
132     update(root*2+1, nstart, mid, ustart, uend, addVal);
133     update(root*2+2, mid+1, nend, ustart, uend, addVal);
134     //根据左右子树的值回溯更新当前节点的值
135     segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val);
136 }
137 
138 
139 int main(){
140     //建树
141     build(0,arr,0,5); 
142     //printTree();
143     //cout<<query(0,0,5,0,3)<<endl; 
144     //updateOne(0,0,5,3,6);//将第3+1哥元素的值增加6 
145     //printTree();
146     update(0,0,5,0,2,2);//0-2区间的值都增加2 
147     //segTree[1].addMark=2;
148     printTree();
149     cout<<query(0,0,5,0,1)<<endl; 
150     printTree();
151     
152     return 0;
153 } 
154 
155 void printTree(){
156     for(int i=0;i<15;i++){
157         cout<<segTree[i].val<<" ";
158     }    
159     cout<<endl;
160 }

 

 

自己代码：

  1 #include <bits/stdc++.h>
  2 #define INFINITE 0x3fffffff
  3 using namespace std;
  4 struct node{
  5     int val;
  6     int addMark;
  7 }tree[100];
  8 int a[6]={2, 5, 1, 4, 9, 3};
  9 
 10 struct node2{
 11     int val;
 12     int start;
 13     int end;
 14 }tree2[100]; 
 15 
 16 //我建树的时候选择让根节点相等作为退出环境，退出的就是叶子节点
 17 //并且我相当于是个二分查找
 18 //其实DFS建树树从左向右，而左边又是小的
 19 //所以可以保证叶子节点按从左到右排下来就是数组a
 20 //并且都是叶子节点 
 21 //所以叶子节点在数组中的索引就是它的范围 
 22 int build(int root,int nstart,int nend){
 23     if(nstart==nend)  return tree[root].val=a[nstart];    
 24     else{
 25         int mid=(nstart+nend)/2;
 26         int left=build(2*root+1,nstart,mid);
 27         int right=build(2*root+2,mid+1,nend);//mid忘记+1了，二分查找有问题 
 28         return tree[root].val=min(left,right);
 29     }
 30 }
 31 
 32 void build2(int root,int nstart,int nend){
 33     cout<<root<<" "<<nstart<<" "<<nend<<" "<<endl;
 34     if(nstart==nend)  tree[root].val=a[nstart];    
 35     else{
 36         int mid=(nstart+nend)/2;
 37         build2(2*root+1,nstart,mid);//写成build 
 38         build2(2*root+2,mid+1,nend);
 39         tree[root].val=min(tree[2*root+1].val,tree[2*root+2].val);
 40     }
 41 }
 42 
 43 void build3(int root,int nstart,int nend){
 44     tree2[root].start=nstart;
 45     tree2[root].end=nend;
 46     if(nstart==nend)  tree[root].val=a[nstart];    
 47     else{
 48         int mid=(nstart+nend)/2;
 49         build3(2*root+1,nstart,mid);//写成build 
 50         build3(2*root+2,mid+1,nend);
 51         tree[root].val=min(tree[2*root+1].val,tree[2*root+2].val);
 52     }
 53 } 
 54 
 55 
 56 
 57 void updateOne(int root,int nstart,int nend,int index,int addVal){
 58     //先找到节点
 59     if(nstart==nend){
 60         if(nstart==index){
 61             tree[root].val+=addVal;
 62             return;
 63         } 
 64     } else{
 65         int mid=(nstart+nend)/2;
 66         updateOne(2*root+1,nstart,mid,index,addVal);//这里写成了search 
 67         updateOne(2*root+2,mid+1,nend,index,addVal);
 68         tree[root].val=min(tree[2*root+1].val,tree[2*root+2].val);//root写成tree,写代码的时候完全没有注意力 
 69     }
 70 } 
 71 
 72 void pushDown(int root){
 73     if(tree[root].addMark!=0){
 74         tree[root*2+1].addMark += tree[root].addMark;
 75         tree[root*2+2].addMark += tree[root].addMark;    
 76         tree[root*2+1].val += tree[root].addMark;    
 77         tree[root*2+2].val += tree[root].addMark;
 78         tree[root].addMark=0;    
 79     }
 80 }
 81 
 82 void update(int root,int nstart,int nend,int qstart,int qend,int addVal){
 83     if(qend<nstart||nend<qstart){
 84         return;
 85     }else if(qstart<=nstart&&nend<=qend){
 86         tree[root].val+=addVal;
 87         tree[root].addMark+=addVal;
 88         return;
 89     }
 90     pushDown(root);
 91     int mid=(nstart+nend)/2;
 92     update(2*root+1,nstart,mid,qstart,qend,addVal);
 93     update(2*root+2,mid+1,nend,qstart,qend,addVal);    
 94     tree[root].val=min(tree[2*root+1].val,tree[2*root+2].val);
 95 }
 96 
 97 
 98 int search(int root,int nstart,int nend,int qstart,int qend){
 99     //cout<<root<<" "<<nstart<<" "<<nend<<" "<<endl;
100     if(qend<nstart||nend<qstart){//这里的小于号写成大于号，画图，画图都看错 
101         return INFINITE;
102     }else if(qstart<=nstart&&nend<=qend){
103         return tree[root].val;
104     }
105     pushDown(root);
106     //把这部分加进else了 
107     int mid=(nstart+nend)/2;
108     int left=search(2*root+1,nstart,mid,qstart,qend);
109     int right=search(2*root+2,mid+1,nend,qstart,qend);
110     return min(left,right);
111     
112 }
113 
114 void print(){
115     for(int i=0;i<=16;i++){
116         cout<<tree[i].val<<" ";
117     } 
118     cout<<endl; 
119 }
120 
121 int main(){
122     //build(0,0,5);
123     build(0,0,5);
124     cout<<search(0,0,5,3,5)<<endl;
125     //updateOne(0,0,5,3,2);
126     update(0,0,5,0,2,2);
127     print();
128     cout<<search(0,0,5,0,0)<<endl;
129     print();
130     return 0;
131 }

自己注意点：

1、所以可以保证叶子节点按从左到右排下来就是数组a，所以叶子节点在数组中的索引就是它的范围 

我建树的时候选择让根节点相等作为退出环境，退出的就是叶子节点
并且我相当于是个二分查找
其实DFS建树树从左向右，而左边又是小的
所以可以保证叶子节点按从左到右排下来就是数组a
并且都是叶子节点
所以叶子节点在数组中的索引就是它的范围

 

2、建树时，二分查找忘记写mid+1

int right=build(2*root+2,mid+1,nend);//mid忘记+1了，二分查找有问题 

 

3、递归函数写错，这个错误在上面代码出现5+次，把update写错成search

build2(2*root+1,nstart,mid);//写成build 

在build2的递归中把build2写成build

 

4、root写成tree,写代码的时候完全没有注意力 

tree[root].val=min(tree[2*root+1].val,tree[2*root+2].val);//root写成tree,写代码的时候完全没有注意力 

 

5、

if(qend<nstart||nend<qstart){//这里的小于号写成大于号，画图，画图都看错 

 

6、延迟标记的search更新还是需要看

 

posted @ 2017-09-11 23:36  范仁义  阅读(2233)  评论(0)  编辑  收藏  举报