区间覆盖(线段树)
区间覆盖(线段树)
打赏
X轴上方有若干条平行于X轴的线段,求这些线段能够覆盖X轴的总长度?
输入格式
第一行一个数n(n<=100000),表示线段个数;
接下来n行,每行两个整数a[i],b[i](-10^8<=a[i],b[i]<=10^8),代表一个线段的两个端点输出覆盖X轴的长度
输入样例
2
10 12
2 4
输出样例
4

1 /* 2 样例: 3 有两段线 4 1 2 5 2 3 6 */ 7 8 #include <bits/stdc++.h> 9 using namespace std; 10 void print(); 11 struct node{ 12 int start,end; 13 int cover; 14 }segTree[100]; 15 16 //创建线段树 17 void build(int root,int start,int end){ 18 segTree[root].start=start; 19 segTree[root].end=end; 20 segTree[root].cover=0; 21 if(start+1<end){ 22 int mid=(start+end)/2; 23 build(2*root,start,mid); 24 build(2*root+1,mid,end); 25 } 26 } 27 28 //1-4怎么办 29 //插入线段,线段的左右端点分别为left和right 30 void insert(int root,int left,int right){ 31 //这里还是空的才需要插入 32 if(segTree[root].cover==0){ 33 int mid=(segTree[root].start+segTree[root].end)/2; 34 if(left==segTree[root].start&&right==segTree[root].end){ 35 segTree[root].cover=1; 36 } 37 else if(right<mid){//去左子树中找 38 insert(2*root,left,right); 39 } 40 else if(left>mid){//去右子树中找 41 insert(2*root+1,left,right); 42 } 43 else{//如果没有正好合适的,就把区间给拆了 44 insert(2*root,left,mid); 45 insert(2*root+1,mid,right); 46 } 47 } 48 } 49 50 51 int count(int root){ 52 if(segTree[root].cover==1){ 53 return segTree[root].end-segTree[root].start; 54 } 55 //又不等于1,又是叶子节点,肯定给你退出 56 else if(segTree[root].end-segTree[root].start==1){ 57 return 0; 58 } 59 else{ 60 return count(2*root)+count(2*root+1); 61 } 62 } 63 64 int main(){ 65 build(1,1,5); 66 print(); 67 insert(1,1,4); 68 //insert(1,2,3); 69 print(); 70 //cout<<count(1)<<endl; 71 return 0; 72 } 73 74 void print(){ 75 for(int i=1;i<=7;i++){ 76 cout<<segTree[i].start<<" "<<segTree[i].end<<" "<<segTree[i].cover<<endl; 77 } 78 cout<<"-------------------------------------------------------------------------"<<endl; 79 }
再贴一份代码,上面那段代码insert位置有问题
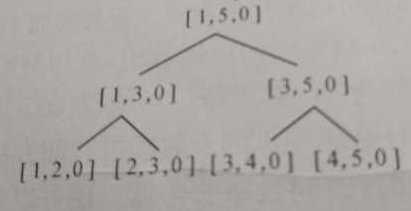
1 #include <bits/stdc++.h> 2 using namespace std; 3 struct node{ 4 int val; 5 int start; 6 int end; 7 }tree[100]; 8 9 void print(); 10 11 void build(int root,int start,int end){ 12 //这里是线段有没有覆盖,所以叶子节点是线段而不是点 13 tree[root].start=start; 14 tree[root].end=end; 15 tree[root].val=0; 16 if(start+1<end){ 17 int mid=(start+end)/2; 18 build(2*root,start,mid); 19 build(2*root+1,mid,end); 20 } 21 } 22 23 void insert(int root,int left,int right){ 24 if(tree[root].val==0){ 25 int start=tree[root].start; 26 int end=tree[root].end; 27 int mid=(start+end)/2; 28 cout<<start<<" "<<end<<endl; 29 if(start==left&&end==right){ 30 tree[root].val=1; 31 } 32 else if(start+1==end){ 33 return ; 34 } 35 else if(mid<left){ 36 insert(2*root+1,left,right); 37 } 38 else if(right<mid){ 39 insert(2*root,left,right); 40 } 41 else{ 42 insert(2*root,left,mid); 43 insert(2*root+1,mid,right); 44 } 45 } 46 } 47 48 int count(int root){ 49 int start=tree[root].start; 50 int end=tree[root].end; 51 int val=tree[root].val; 52 if(val==1){ 53 return end-start; 54 } 55 else if(end-start==1){ 56 return 0; 57 } 58 else{ 59 return count(root*2)+count(root*2+1); 60 } 61 } 62 63 int main(){ 64 build(1,1,5); 65 print(); 66 insert(1,1,4); 67 print(); 68 cout<<count(1)<<endl; 69 return 0; 70 71 } 72 73 void print(){ 74 for(int i=1;i<=7;i++){ 75 cout<<tree[i].start<<" "<<tree[i].end<<" "<<tree[i].val<<endl; 76 } 77 cout<<endl; 78 }
版权申明:欢迎转载,但请注明出处
一些博文中有一些参考内容因时间久远找不到来源了没有注明,如果侵权请联系我删除。
在校每年国奖、每年专业第一,加拿大留学,先后工作于华东师范大学和香港教育大学。
2025-01-31:宅加太忙,特此在网上找女朋友,坐标上海,非诚勿扰,vx:fan404006308
AI交流资料群:753014672






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具