P1270 “访问”美术馆

P1270 “访问”美术馆

题目描述

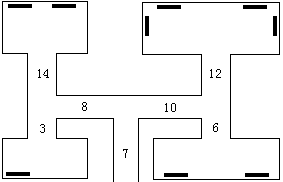
经过数月的精心准备，Peer Brelstet，一个出了名的盗画者，准备开始他的下一个行动。艺术馆的结构，每条走廊要么分叉为两条走廊，要么通向一个展览室。Peer知道每个展室里藏画的数量，并且他精确测量了通过每条走廊的时间。由于经验老到，他拿下一幅画需要5秒的时间。你的任务是编一个程序，计算在警察赶来之前，他最多能偷到多少幅画。

输入输出格式

输入格式：

 

第1行是警察赶到的时间，以s为单位。第2行描述了艺术馆的结构，是一串非负整数，成对地出现：每一对的第一个数是走过一条走廊的时间，第2个数是它末端的藏画数量；如果第2个数是0，那么说明这条走廊分叉为两条另外的走廊。数据按照深度优先的次序给出，请看样例。

一个展室最多有20幅画。通过每个走廊的时间不超过20s。艺术馆最多有100个展室。警察赶到的时间在10min以内。

 

输出格式：

 

输出偷到的画的数量

 

输入输出样例

输入样例#1：

60
7 0 8 0 3 1 14 2 10 0 12 4 6 2

输出样例#1：

2

 

 

分析：

首先，审题是关键。只有读懂了题意，才可能写出正确的程序。可以说，这一道题目的输入是一个亮点。因为它不同于平常的读入，而是用深度优先搜索的方式读入。所以，编程人需要非常熟悉深搜，才可能正确地导入数据。

就算读入了数据，许多同学还是不能把握好。因为这道题目的数据量看似不大，所以有些同学可能会陷入搜索的死胡同。其实本题的数据量还是很大的，因为每条路的走廊也需要时间。所以，会让人没有头绪。

 

其实，题目已经把条件给的很清楚了，艺术馆的结构，每条走廊要么分叉为两条走廊，要么通向一个展览室。显然，美术馆就是一颗树，而且是一颗二叉树。那么，说到二叉树，又说到最优解，那么思路就很明显了——树形动规。

 

f[node][time]表示node点花time时间最多拿的画的数量

转移的时候 如果当前节点是子节点，就判断能取多少

如果不是就枚举当前节点所分配给左树的时间，由左右子树的和转移来。

f[root][time]=max(f[root][time],f[left][lctime]+f[right][time-limit-lctime]);

 

 

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1001
using namespace std;
int n,cnt,tot;
int f[maxn][maxn];
void dfs()
{
    //root默认为1号节点 
    int root=++cnt,limit,time;
    scanf("%d%d",&limit,&tot);
    limit<<=1;
    //转移的时候 如果当前节点是子节点，就判断能取多少
    if(tot)//子节点 
    {
        for(int time=limit;time<=n;time++)//取一幅画要5秒 
          f[root][time]=min((time-limit)/5,tot);//判断取多少 
    }
    //如果不是就枚举当前节点所分配给左树的时间，由左右子树的和转移来。 
    else
    {
        int left=cnt+1,right;dfs();//左节点是cnt+1 
        //而且count本身没有加，并且我们没有把left传过去，我们用的还是count
        //所以左节点是父亲节点的后一个 
        right=cnt+1;dfs();//left和right中间有个dfs，会读入很多数据，所以left和right会相差很大 
        for(int time=limit;time<=n;time++)
          for(int lctime=0;lctime<=time-limit;lctime++)//分配给左树的时间 
          {
              f[root][time]=max(f[root][time],f[left][lctime]+f[right][time-limit-lctime]);//左右子树的和 
          }
    }
}
int main()
{
    //因为是警察到来之前，所以-1 
    scanf("%d",&n);n--;
    dfs();
    printf("%d\n",f[1][n]);
    return 0;
}