P1043 数字游戏

P1043 数字游戏

题目描述

丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的，在你面前有一圈整数（一共n个），你要按顺序将其分为m个部分，各部分内的数字相加，相加所得的m个结果对10取模后再相乘，最终得到一个数k。游戏的要求是使你所得的k最大或者最小。

例如，对于下面这圈数字（n=4，m=2）：

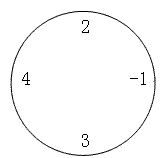
要求最小值时，((2-1) mod 10)×((4+3) mod 10)=1×7=7，要求最大值时，为((2+4+3) mod 10)×(-1 mod 10)=9×9=81。特别值得注意的是，无论是负数还是正数，对10取模的结果均为非负值。

丁丁请你编写程序帮他赢得这个游戏。

输入输出格式

输入格式：

 

输入文件第一行有两个整数，n（1≤n≤50）和m（1≤m≤9）。以下n行每行有个整数，其绝对值不大于104，按顺序给出圈中的数字，首尾相接。

 

输出格式：

 

输出文件有两行，各包含一个非负整数。第一行是你程序得到的最小值，第二行是最大值。

 

输入输出样例

输入样例#1：

4 2
4
3
-1
2

输出样例#1：

7
81

 

 

思路：

思路一：

状态：

把环拆成链，枚举开始位置（O（n）^4）

d[i][j]表示前i个数分成j部分的最优值

状态转移方程：

d[i][j]=opt(d[i][j],d[k][j-1]*(((s[i]-s[k])%10+10)%10))

s[i]是前i个数的和

边界：

d[0][0]=1;

d[i][1]=((s[i]%10+10)%10)

 

思路二：

把环看成两倍的线性长  （O（n）^3）

 

思路三：

%n 对n取模 （O（n）^3）

这种的话状态转移方程f[i][j]，i表示起点，j表示长度

 

#include<cstdio>
#include<algorithm>
using namespace std;

int n,m,Max,Min,s[55],d[55][10],dp[55][10];
void DP(int a[])
{
    int i,j,k;
    for(i=1;i<=n;i++)
        s[i]=s[i-1]+a[i];
    for(i=0;i<=n;i++)
        for(j=0;j<=m;j++)
        {
            d[i][j]=0;
            dp[i][j]=-1u>>1;
        }
    d[0][0]=dp[0][0]=1;
    for(i=1;i<=n;i++)
        d[i][1]=dp[i][1]=(s[i]%10+10)%10;
    for(j=2;j<=m;j++)
        for(i=j;i<=n;i++)
            for(k=j-1;k<i;k++)
            {
                d[i][j]=max(d[i][j],d[k][j-1]*(((s[i]-s[k])%10+10)%10));//第k+1个数到第i个数分到第j部分
                dp[i][j]=min(dp[i][j],dp[k][j-1]*(((s[i]-s[k])%10+10)%10));
            }    
    Max=max(Max,d[n][m]);
    Min=min(Min,dp[n][m]);
}
int main()
{    
    while(scanf("%d%d",&n,&m)==2)
    {
        int i,j,a[105];
        Max=0;
        Min=-1u>>1;
        for(i=1;i<=n;i++)
        {
            scanf("%d",a+i);
            a[n+i]=a[i];
        }
        for(j=0;j<n;j++)
            DP(a+j);
        printf("%d\n%d\n",Min,Max);        
    }
}