DP的四边形优化
DP的四边形优化
一、进行四边形优化需要满足的条件
1、状态转移方程如下:
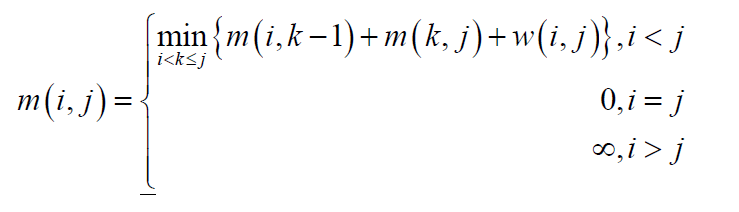
m(i,j)表示对应i,j情况下的最优值。
w(i,j)表示从i到j的代价。
例如在合并石子中:
m(i,j)表示从第i堆石子合并到j堆石子合并成一堆的最小代价。
w(i,j)表示从第i堆石子到第j堆石子的重量和。
2、函数w满足区间包含的单调性和四边形不等式

二、满足上述条件之后的两条定理
1、假如函数w满足上述条件,那么函数m 也满足四边形不等式,即
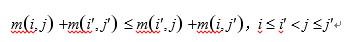
例如:
假如有:w(1, 3) + w(2, 4) £ w(2, 3) + w(1, 4),
m(1, 3) + m(2, 4) £ m(2, 3) + m(1, 4),
2、假如m(i, j)满足四边形不等式,那么s (i, j)单调,即:
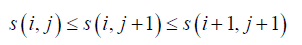
三、如何使用
运用上面两条定理,可以将最上面的DP状态转移方程变为如下:
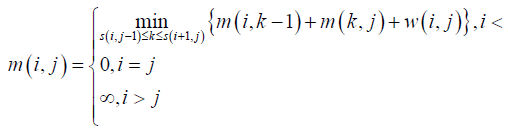
四、具体应用
用四边形优化将合并石子(直线型)的时间复杂度化为 O(n*n)
1 #include <iostream> 2 #include <string.h> 3 #include <stdio.h> 4 5 using namespace std; 6 const int INF = 1 << 30; 7 const int N = 1005; 8 9 int dp[N][N]; 10 int p[N][N]; 11 int sum[N]; 12 int n; 13 14 int getMinval() 15 { 16 for(int i=1; i<=n; i++) 17 { 18 dp[i][i] = 0; 19 p[i][i] = i; 20 } 21 for(int len=1; len<n; len++) 22 { 23 for(int i=1; i+len<=n; i++) 24 { 25 int end = i+len; 26 int tmp = INF; 27 int k = 0; 28 for(int j=p[i][end-1]; j<=p[i+1][end]; j++) 29 { 30 if(dp[i][j] + dp[j+1][end] + sum[end] - sum[i-1] < tmp) 31 { 32 tmp = dp[i][j] + dp[j+1][end] + sum[end] - sum[i-1]; 33 k = j; 34 } 35 } 36 dp[i][end] = tmp; 37 p[i][end] = k; 38 } 39 } 40 return dp[1][n]; 41 } 42 43 int main() 44 { 45 while(scanf("%d",&n)!=EOF) 46 { 47 sum[0] = 0; 48 for(int i=1; i<=n; i++) 49 { 50 int val; 51 scanf("%d",&val); 52 sum[i] = sum[i-1] + val; 53 } 54 printf("%d\n",getMinval()); 55 } 56 return 0; 57 }
上述代码具体在内存中的运行过程:




