搜索5--noi1700:八皇后问题

搜索5--noi1700:八皇后问题

一、心得

 

二、题目

1700:八皇后问题

• 查看
• 提交
• 统计
• 提问

总时间限制: 

10000ms

 

内存限制: 

65536kB

描述

在国际象棋棋盘上放置八个皇后，要求每两个皇后之间不能直接吃掉对方。

输入

无输入。

输出

按给定顺序和格式输出所有八皇后问题的解（见Sample Output）。

样例输入

样例输出

No. 1
1 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 0 0 1 0 0 0 
0 0 0 0 0 0 0 1 
0 1 0 0 0 0 0 0 
0 0 0 1 0 0 0 0 
0 0 0 0 0 1 0 0 
0 0 1 0 0 0 0 0 
No. 2
1 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 0 1 0 0 0 0 
0 0 0 0 0 1 0 0 
0 0 0 0 0 0 0 1 
0 1 0 0 0 0 0 0 
0 0 0 0 1 0 0 0 
0 0 1 0 0 0 0 0 
No. 3
1 0 0 0 0 0 0 0 
0 0 0 0 0 1 0 0 
0 0 0 0 0 0 0 1 
0 0 1 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 0 1 0 0 0 0 
0 1 0 0 0 0 0 0 
0 0 0 0 1 0 0 0 
No. 4
1 0 0 0 0 0 0 0 
0 0 0 0 1 0 0 0 
0 0 0 0 0 0 0 1 
0 0 0 0 0 1 0 0 
0 0 1 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 1 0 0 0 0 0 0 
0 0 0 1 0 0 0 0 
No. 5
0 0 0 0 0 1 0 0 
1 0 0 0 0 0 0 0 
0 0 0 0 1 0 0 0 
0 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 
0 0 1 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 0 1 0 0 0 0 
No. 6
0 0 0 1 0 0 0 0 
1 0 0 0 0 0 0 0 
0 0 0 0 1 0 0 0 
0 0 0 0 0 0 0 1 
0 1 0 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 1 0 0 0 0 0 
0 0 0 0 0 1 0 0 
No. 7
0 0 0 0 1 0 0 0 
1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 
0 0 0 1 0 0 0 0 
0 1 0 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 1 0 0 0 0 0 
0 0 0 0 0 1 0 0 
No. 8
0 0 1 0 0 0 0 0 
1 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 0 0 1 0 0 0 
0 0 0 0 0 0 0 1 
0 1 0 0 0 0 0 0 
0 0 0 1 0 0 0 0 
0 0 0 0 0 1 0 0 
No. 9
0 0 0 0 1 0 0 0 
1 0 0 0 0 0 0 0 
0 0 0 1 0 0 0 0 
0 0 0 0 0 1 0 0 
0 0 0 0 0 0 0 1 
0 1 0 0 0 0 0 0 
0 0 0 0 0 0 1 0 
0 0 1 0 0 0 0 0 
...以下省略

提示

此题可使用函数递归调用的方法求解。

来源

计算概论05

三、分析

DFS经典题目

 

四、AC代码

//1700:八皇后问题
/*
1、首先分析输出样例的顺序
  选第一行，选第二行
  按行的顺序
  说明是指定了列，让我们来填行 
*/ 
#include <iostream>
using namespace std;
//用来存储方案 ,下标都是从1开始 
int a[9][9]; 
int visRow[9]; //行
int visLeftIncline[17];//左斜线 使用的时候 row+column 
int visRightIncline[16]; //右斜线，使用的时候row-column+8 
int ansCount=0;

void init(){
    
}

void print(){
    cout<<"No. "<<(++ansCount)<<endl;
    for(int i=1;i<=8;i++){
        for(int j=1;j<=8;j++){
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
    
} 

void search(int column){
    if(column>8){
        //if(ansCount>=5) return;
        print();
        //cout<< ansCount<<endl;
    }
    else{
        for(int row=1;row<=8;row++){
            if(!visRow[row]&&!visLeftIncline[row+column]&&!visRightIncline[row-column+8]){
                visRow[row]=1;
                visLeftIncline[row+column]=1;
                visRightIncline[row-column+8]=1;
                a[row][column]=1;
                search(column+1);//找下一列
                //回溯 
                visRow[row]=0;
                visLeftIncline[row+column]=0;
                visRightIncline[row-column+8]=0;
                a[row][column]=0; 
            }
        }
    }
}

int main(){
    init(); 
    search(1);
    return 0;
} 

 

 

五、注意点

1、注意回溯里面的return

return语句总是返回到调用这个函数的父函数

而在回溯中

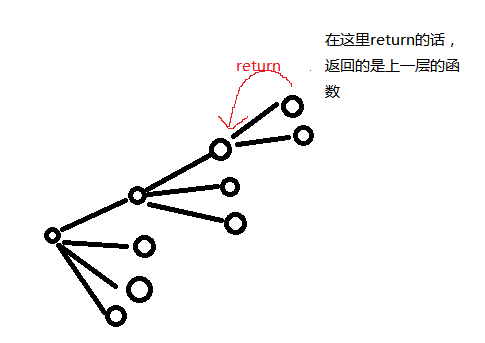
所以在最后面层的return是绝对不会影响到其他函数的计算结果和输出结果的

在以后每次输出结果的时候做一个判断，就能控制结果的输出了