统计学习方法笔记---1203、统计学习方法总结（3.学习策略、4.学习算法）

统计学习方法笔记---1203、统计学习方法总结（3.学习策略、4.学习算法）

一、总结

一句话总结：

反复验证：英语还是读出来的，也就是用和读

 

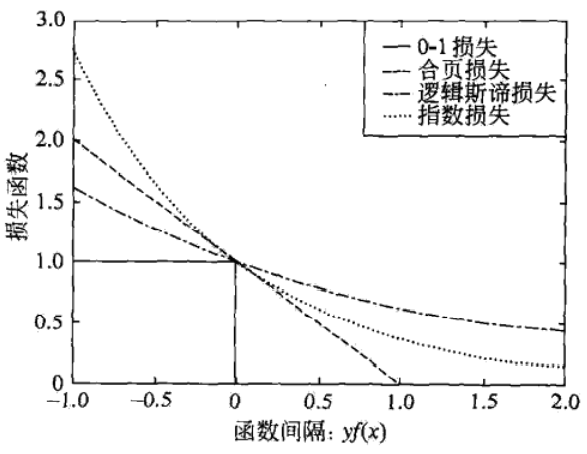
1、支持向量机、逻辑斯谛回归与最大熵模型、提升方法 这3种损失函数都是【0-1损失函数】的上界，具有相似的形状？

支持向量机：【合页损失函数】：$$[ 1 - y f ( x ) ] _ { + }$$

逻辑斯谛回归与最大熵模型：【逻辑斯谛损失函数】：$$\log [ 1 + \exp ( - y f ( x ) ) ]$$

提升方法：【指数损失函数】：$$\exp ( - y f ( x ) )$$

 

 

 

2、统计学习方法总结-学习策略？

【概率模型的学习】可以【形式化为极大似然估计或贝叶斯估计的极大后验概率估计】.这时，学习的策略是【极小化对数似然损失】或【极小化正则化的对数似然损失】.对数似然损失可以写成-logP(y|x)极大后验概率估计时，正则化项是先验概率的负对数

【决策树学习】的策略是【正则化的极大似然估计】，损失函数是对数似然损失，正则化项是决策树的复杂度

【逻辑斯谛回归与最大熵模型、条件随机场】的学习策略既可以看成是【极大似然估计（或正则化的极大似然估计）】，又可以看成是【极小化逻辑斯谛损失（或正则化的逻辑斯谛损失）】

【朴素贝叶斯模型、隐马尔可夫模型】的非监督学习也是【极大似然估计或极大后验概率估计】，但这时模型含有【隐变量】

 

3、统计学习方法总结-学习方法-1？

1、统计学习的问题有了具体的形式以后，就变成了【最优化问题】.有时，最优化问题比较简单，【解析解】存在，最优解可以由公式简单计算，但在多数情况下，最优化问题【没有解析解】，需要用数值计算的方法或启发式的方法求解

2、【朴素贝叶斯法与隐马尔可夫模型】的监督学习，【最优解即极大似然估计值】，可以由概率计算公式直接计算

3、【感知机、逻辑斯谛回归与最大熵模型、条件随机场】的学习利用【梯度下降法、拟牛顿法等】.这些都是一般的无约束最优化问题的解法.

4、【支持向量机】学习，可以解【凸二次规划的对偶问题】、【有序列最小最优化算法等、方法

 

4、统计学习方法总结-学习方法-2？

5、【决策树】学习是基于【启发式】算法的典型例子.可以认为【特征选择、生成、剪枝】是启发式地进行正则化的【极大似然估计】

6、【提升方法】利用学习的模型是加法模型、损失函数是指数损失函数的特点，启发式地从前向后逐步学习模型，以达到【逼近优化目标函数】的目的

7、【EM算法】是一种【迭代】的求解含【隐变量】概率模型参数的方法，它的收敛性可以保证，但是【不能保证收敛到全局最优】

8、【支持向量机学习、逻辑斯谛回归与最大熵模型学习、条件随机场学习】是【凸优化问题】，【全局最优解保证存在】.而其他学习问题则不是凸优化问题

 

 

 

二、内容在总结中

博客对应课程的视频位置：