蒙特卡洛树简单介绍
蒙特卡洛树简单介绍
一、总结
一句话总结:
2006年,Remi Coulom开发了一款叫做【Crazy Stone的围棋游戏】,该款游戏表现令人惊讶,斩获了好几个锦标赛冠军。【蒙特卡洛树就是该游戏的一个核心算法】。
从全局来看,蒙特卡洛树搜索的主要目标是:【给定一个游戏状态来选择最佳的下一步】。
1、Alpha Go/Zero的核心组件包括?
【蒙特卡洛树搜索】——【使用PUCT函数的一种树遍历的特定变体】
【残差卷积神经网络】——【使用policy network(策略网络)和value network(价值网络)来进行比赛的评估和落子先验概率的估计】
【强化学习】——【通过自我对局来训练网络】
2、蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)运行所在的框架/环境是一个游戏,它本身是一个非常抽象和宽泛的概念,因此这里我们只关注一种游戏类型:【双人有限零和顺序游戏】?
【游戏】:意味着我们在一种需要【交互的情境】中,交互通常会涉及一个或多个角色;【有限】:表明在任意时间点,角色之间存在的【交互方式都是有限的】
【双人】:游戏中只有【两个角色】;【顺序】:【玩家依次交替】进行他们的动作
【零和】:【参与游戏的两方有完全相反的目标】,换句话说就是,【游戏的任意结束状态双方的收益之和等于零】
我们可以很轻松的验证,围棋、国际象棋和井字棋都是双人有限零和顺序游戏:【有两位玩家参与,玩家能进行的动作总是有限的,双方的游戏目标是完全相反的(所有游戏的结果之和等于0)】。
3、如何表示一个游戏?
在一本博弈论的书中,你也许会找到如下定义:定义:一个广义形式的游戏可以有一个元组定义:$$\\\Gamma_E=\{\mathcal{X,A},I,p,\alpha,\mathcal{H},H,\imath,\rho,u \} $$
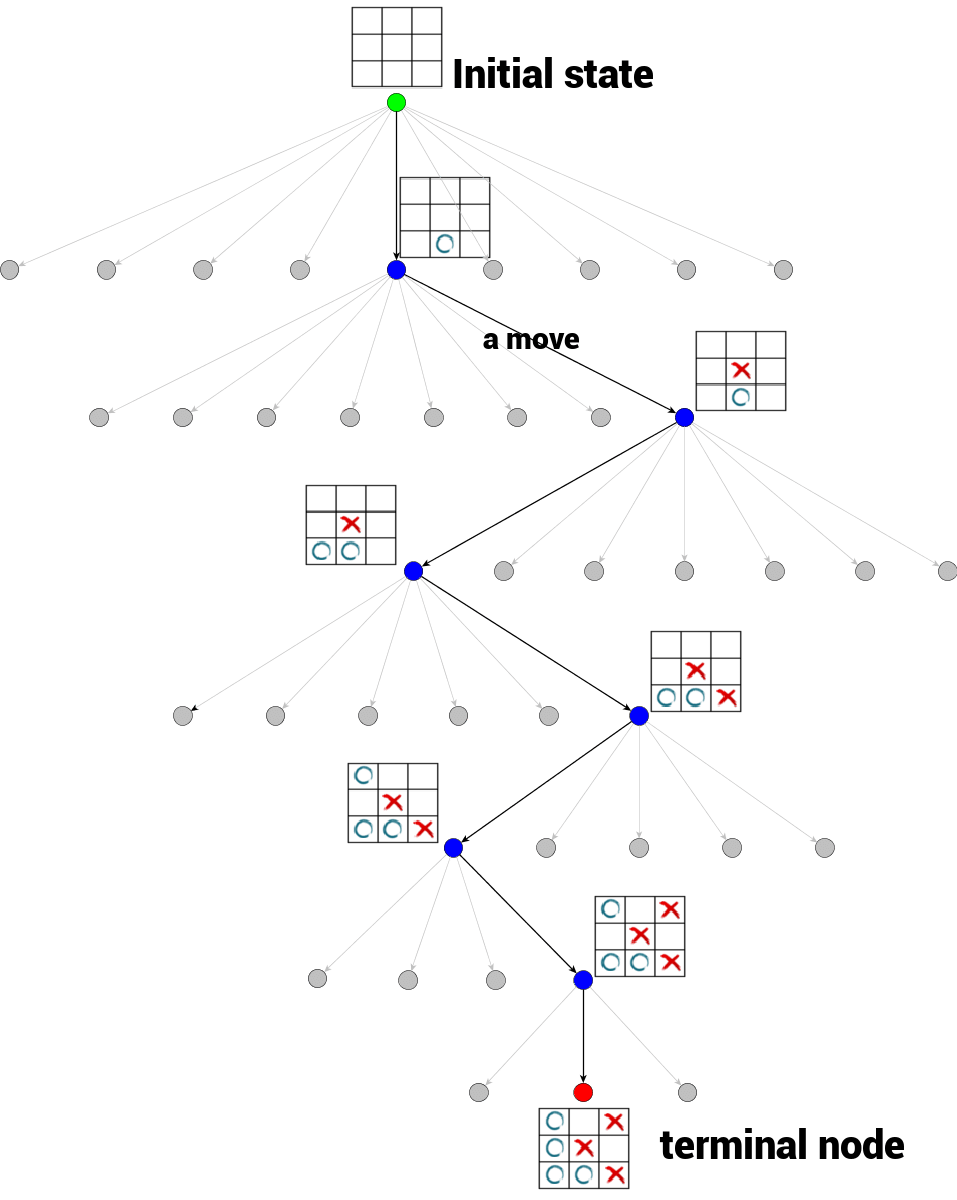
我们可以用一种【常见的数据结构以来表示游戏——游戏树】。
游戏树是一个树,其中【每一个节点代表游戏的一个确定状态】。从一个节点到该节点的一个子节点(如果存在)是一个移动。节点的子节点数目称为分支因子。【游戏树的根节点代表游戏的初始状态。游戏树的终端节点是没有子节点的节点,至此游戏结束,无法再进行移动】。终端节点的状态也就是游戏的结果(输/赢/平局)。
4、什么是“最佳的下一步”?
【游戏树是一种递归的数据结构】,每次选择完最佳的下一步时,会移动到下一个子节点,而这个子节点又是它子树的根节点。【因此我们可以把一局游戏视为“最佳下一步”的一个问题序列】,每一次都可以由一个不同根节点的游戏树表示。通常在实际应用中,【我们不需要记住到当前状态的路径,因为这不是当前游戏状态的关注点】。
关于这个问题并没有直接的答案。首先,我们根本无法提前知道对手的策略,对手可能是一个职业选手或者只是个并不怎么样的业余选手。【以国际象棋为例,如果你的对手是一个业余选手,你也许可以选择简单的策略来欺骗他并迅速获得胜利。但是如果遇上很强的对手,仍然使用这个策略,情况可能就反过来了】。
如果你完全不了解你的对手,这里有一个【非常极端的策略,称为minmax】。这个策略【就是假设你的对手每一步都使用最优的策略】,然后最大化你的游戏收益。
5、minmax策略:就是假设你的对手每一步都使用最优的策略?
$$v _ { A } ( s _ { i } ) = \max _ { a _ { i } } v _ { B } ( \operatorname { move } ( s _ { i } , a _ { i } ) ) \quad v _ { A } ( \hat { s } ) = \operatorname { eval } ( \hat { s } )$$
$$v _ { B } ( s _ { i } ) = \min _ { a _ { i } } v _ { A } ( \operatorname { move } ( s _ { i } , a _ { i } ) ) \quad v _ { B } ( \hat { s } ) = - \operatorname { eval } ( \hat { s } )$$
其中,【v_A和v_B是玩家A和B的效益函数】,【move是给定当前状态s_i和该状态下的动作a_i产生下一个游戏状态的函数】,eval是评估最终游戏状态的函数,\hat{s}是任意一个终端游戏状态。
简单来说,【给定一个状态s,你想要找到一个动作a_i能够获得最大回报(假设你对手总是在最小化你的收益)】,这也是【minmax算法的由来】。我们所需要做的只是展开整个游戏树,并根据递归公式(1)来进行反向传播。
6、蒙特卡洛树搜索(MCTS)——基本概念?
MCTS对游戏进行【多次模拟】,然后【尝试基于模拟结果对最佳下一步进行预测】。
【MCTS的主要概念还是搜索】。搜索是沿着游戏树的一组遍历的集合,【单次遍历是从根节点(当前游戏状态)到一个未完全展开节点的路径】。
一个未完全展开的节点意味着它至少有一个未被访问的子节点。【当遇到未完全展开的节点时,从该节点的子节点中选取一个未被访问过的用来进行一次模拟】。
模拟的结果然后反向转播是当前树的根节点,并更新节点的统计信息。【当搜索结束时(受限于时间或计算能力),就可以根据收集的统计信息来决定下一步怎么走】。
7、我们应该【什么时候结束】蒙特卡洛树搜索(MCTS)过程?
【它取决于上下文】。如果你考虑搭建一个游戏引擎,【那么你的“思考时间”可能是有限的,计算能力也是有限的】。因此最保险的做法是在【你资源允许的情况下尽可能久地运行MCTS】。
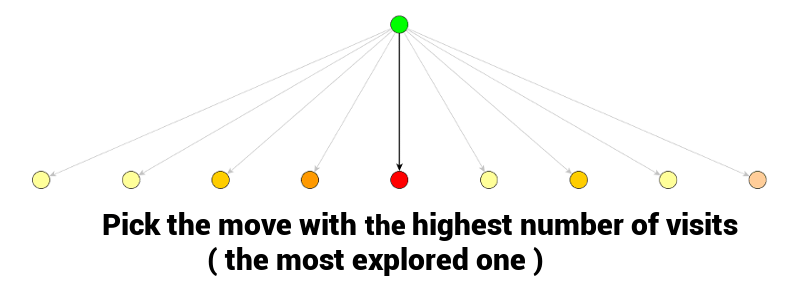
当MSCT程序结束时,最佳的移动通常是【访问次数最多的那个节点】。
二、蒙特卡洛树简单介绍
转自或参考:蒙特卡洛树搜索(新手教程)
https://blog.csdn.net/qq_16137569/article/details/83543641
本篇博客为《Monte Carlo Tree Search – beginners guide》的翻译的总结,水平有限,有兴趣的朋友可以直接阅读原文。