201116西瓜书机器学习系列---12、计算学习理论

201116西瓜书机器学习系列---12、计算学习理论

一、总结

一句话总结：

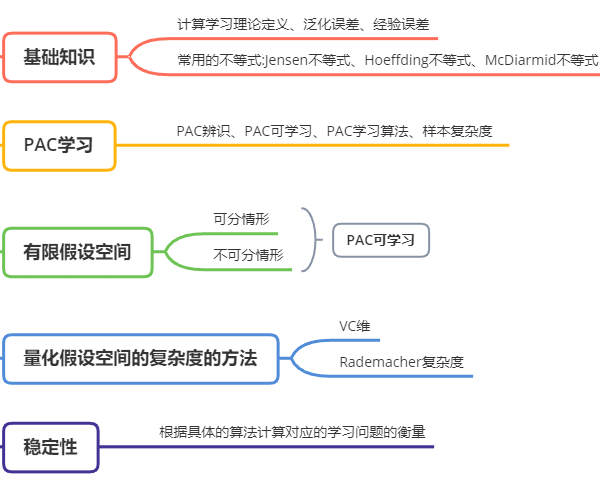
计算学习理论：研究【泛化误差】和【经验误差】之间的【逼近程度】

 

 

 

1、PAC可学习？

PAC可学习：以较大概率【预测】到【满足预测误差上限】的模型

 

2、量化假设空间的复杂度的方法？

【VC维和Rademacher复杂度】

 

3、计算学习理论：研究【经验误差】和【泛化误差】之间的逼近程度？

【已知数据集上的误差】称为经验误差，【全局数据集上的误差】称为泛化误差

【泛化误差】是我们【追求的目标】，【经验误差】是我们【已有数据集上的表现】；两者之间的逼近程度反应了【模型的准确度】或者说【模型的可用程度】

 

 

 

4、PAC可学习（以较大概率【预测】到【满足预测误差上限】的模型） 三个重要概念？

概念类：【目标概念】构成的【集合】；描述【数据】是【怎样生成】的

学习算法：例如【线性回归、逻辑回归、SVM等】

假设空间：学习算法的【所有可能的概念】的【集合】，例如线性回归里面y=5x+2和y=3x+5都属于假设空间里面的概念

 

 

5、PAC可学习：有限假设空间：①可分②不可分；在一定的条件下都是可学习的？

可分：目标概念【在假设空间中】；【不可分】：目标概念【不在】假设空间中

只有【理想情况】下是【可分】的，大部分【实际应用】都是【不可分】的

例如：预测某文章的点击率，实际点击的情况【受影响因素太多了】比如内容质量、推荐精准度，网速流畅程度、天气、用户心情等而假设空间中不可能把所有情况都假设进来

进一步验证【可分或者不可分在一定条件下都是可学习的】，否则算法工程师就失业了

 

6、VC维是什么？

用来【度量假设空间H（模型）的复杂度】：$$VC ( H ) = \max \{ m : \Pi _ { H } ( m ) = 2 ^ { m } \}$$

VC维规律：【参数越多，VC维越大，模型容量大，表达能力强】，VC维度用来表达【模型的容量】

 

 

 

7、常见模型的模型容量？

一般按照线性模型、逻辑回归、决策树、SVM、深度学习，【模型容量逐步增加】

 

 

二、内容在总结中

博客对应课程的视频位置：