微信扫一扫打赏支持

通俗易懂理解指数分布

通俗易懂理解指数分布

一、总结

一句话总结：

卖包子的时间间隔符合 指数分布
本例中指数分布的意义：如果知道这个时间间隔，老板也好调整自己的服务员人数（时间间隔短，那么需要的服务人员就多，反之需要的就少），优化成本结构。

 

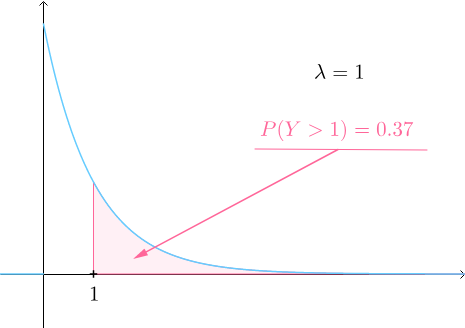
1、当λ较小的时候，比如说λ=1吧，也就是说一天只卖出一个馒头，那么馒头卖出间隔时间大于1的可能性就很大（下图是指数分布的概率密度函数的图像，对应的概率是曲线下面积）？

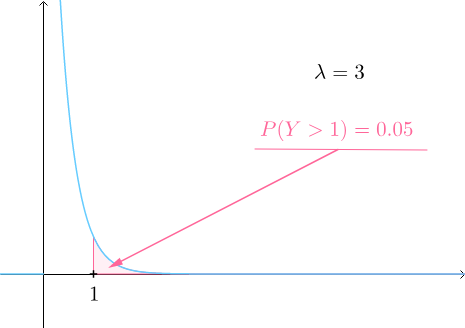
而如果λ较大的时候，比如说λ=3吧，也就是说一天卖出三个馒头，【】那么馒头卖出间隔时间大于1的可能性已经变得很小了】：

 

 

2、每日卖出馒头的数目X服从泊松分布，卖出馒头的时间间隔Y服从指数分布？

【倒数关系】：他们的期望分别为：$$E ( X ) = \lambda , \quad E ( Y ) = \frac { 1 } { \lambda }$$
【倒数关系】：根据之前的分析就比较好理解了，E(X)的含义是平均每日卖出的馒头数，而E(Y)是每个馒头之间卖出的平均时间间隔，所以两者是倒数关系：每日卖出的越多自然间隔时间越短，每日卖出的越少自然间隔时间越长。

 

 

 

二、通俗易懂理解指数分布（转）

转自：https://www.matongxue.com/madocs/2104/

 

指数分布和泊松分布息息相关，所以先简单回忆下之前介绍过的泊松分布。公司楼下有家馒头店，每天早上六点到十点营业：

马同学高等数学

老板统计了一周每日卖出的馒头（为了方便计算和讲解，缩小了数据），想从中找到一些规律：

\begin{array}{c|c} \qquad\qquad&\qquad销售\qquad\\ \hline\color{SkyBlue}{周一}& 3 \\ \hline \color{blue}{周二}& 7 \\ \hline \color{orange}{周三}&4\\ \hline \color{Goldenrod}{周四}&6\\ \hline \color{green}{周五}&5\\ \end{array}

从中可以得到最简单的规律，均值：

\overline{X}=\frac{3+7+4+6+5}{5}=5

这个规律显然不够好，如果把营业时间抽象为一根线段，把这段时间用T来表示：

马同学高等数学

然后把卖出的馒头数画在这根线段上（节约篇幅，只画出周一周二作为示意），可以看到每天卖出的馒头起伏还是很大的：

马同学高等数学
马同学高等数学

经过老板一系列的骚操作（更具体的推导请看如何理解泊松分布），最后得到每日卖出的馒头数X服从泊松分布：

X\sim P(\lambda),\quad \lambda=\overline{X}

泊松分布的具体表达式为：

P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}

据此可以画出每日卖出馒头数的概率分布，这个规律就比均值要精细很多了：

马同学高等数学

2 馒头卖出之间的时间间隔

下面来讨论另外一个问题，馒头卖出之间的时间间隔：

马同学高等数学

可以看出也是随机变量（也就是图中的T_1、T_2、T_3、\cdots），不过相对馒头卖出个数而言，时间间隔肯定是连续的随机变量。

如果知道这个时间间隔，老板也好调整自己的服务员人数（时间间隔短，那么需要的服务人员就多，反之需要的就少），优化成本结构。那么问题来了，这个时间间隔服从什么分布？

3 一天的间隔

既然都是卖馒头的问题，那么还是让我们从已知的泊松分布上想想办法。之前得到的泊松分布让我们知道了每天卖出的馒头数，所以下面按天来分析看看。

假如某一天没有卖出馒头，比如说周三吧，这意味着，周二最后卖出的馒头，和周四最早卖出的馒头中间至少间隔了一天：

马同学高等数学

当然也可能运气不好，周二也没有卖出馒头。那么卖出两个馒头的时间间隔就隔了两天，但无论如何时间间隔都是大于一天的：

马同学高等数学

而某一天没有卖出馒头的概率可以由泊松分布得出：

P(X=0)=\frac{\lambda^0}{0!}e^{-\lambda}=e^{-\lambda}

根据上面的分析，卖出两个馒头之间的时间间隔要大于一天，那么必然要包含没有卖出馒头的这天，所以两者的概率是相等的。如果假设随机变量为：

Y=卖出两个馒头之间的时间间隔

那么就有：

P(Y > 1)=P(X=0)=e^{-\lambda}

4 泊松过程

之前求出的泊松分布实在限制太大，只告诉了我们每天卖出的馒头数。不过没有关系，稍微扩展下可以得到新的函数：

P(X=k,t)=\frac{\left(\lambda t\right)^k}{k!}e^{-\lambda t}

通过新的这个函数就可知不同的时间段内卖出的馒头数的分布了（t=1时就是泊松分布）：

\begin{array}{c|c} \hline \quad \quad &\quad t\quad&\quad PDF\quad\\ \hline \\ 每天卖出的馒头数 & 1 & P(X=k,1)=\frac{\lambda^k}{k!}e^{-\lambda}\\ 半天卖出的馒头数 & \frac{1}{2} & P(X=k,\frac{1}{2})=\frac{\left(\frac{1}{2}\lambda\right)^k}{k!}e^{-\frac{1}{2}\lambda}\\ 三小时卖出的馒头数 & \frac{1}{8} & P(X=k,\frac{1}{8})=\frac{\left(\frac{1}{8}\lambda\right)^k}{k!}e^{-\frac{1}{8}\lambda}\\ \\ \hline \end{array}

扩展后得到的函数称为\color{Salmon}{泊松过程}，这里涉及到比较复杂的知识，就不做推导了，感兴趣的同学可以自行根据关键字扩展学习。

5 指数分布

两次卖出馒头之间的时间间隔大于t的概率，根据之前的分析，等同于t时间内没有卖出一个馒头的概率，而后者的概率可以由泊松过程给出。至此所需的条件都齐备了，那么开始解题吧，假设随机变量：

Y=两次卖出馒头之间的时间间隔

这个随机变量的概率可以如下计算：

P(Y > t)=P(X=0, t)=\frac{\left(\lambda t\right)^0}{0!}e^{-\lambda t}=e^{-\lambda t},\quad t \ge 0

进而有：

P(Y \le t)=1-P(Y > t)=1-e^{-\lambda t}

这其实已经得到了Y的累积分布函数了：

F(y)=P(Y \le y)=\begin{cases} 1-e^{-\lambda y}, & y \ge 0\\ 0,& y < 0 \end{cases}

对其求导就可以得到概率密度函数：

p(y)=\begin{cases} \lambda e^{-\lambda y}, & y \ge 0\\ 0,& y < 0 \end{cases}

这就是卖出馒头的时间间隔Y的概率密度函数，也称为\color{Salmon}{指数分布}。

6 指数分布的图像

指数分布中的\lambda是每日平均卖出的馒头数，如果\lambda越大，也就是说每日卖出的馒头越多，那么两个馒头之间的时间间隔必然越短，这点从图像上也可以看出。

当\lambda较小的时候，比如说\lambda=1吧，也就是说一天只卖出一个馒头，那么馒头卖出间隔时间大于1的可能性就很大（下图是指数分布的概率密度函数的图像，对应的概率是曲线下面积）：

马同学高等数学

而如果\lambda较大的时候，比如说\lambda=3吧，也就是说一天卖出三个馒头，那么馒头卖出间隔时间大于1的可能性已经变得很小了：

马同学高等数学

7 泊松分布与指数分布的期望

每日卖出馒头的数目X服从泊松分布，卖出馒头的时间间隔Y服从指数分布：

X\sim P(\lambda),\quad Y\sim Exp(\lambda)

他们的期望分别为：

E(X)=\lambda,\quad E(Y)=\frac{1}{\lambda}

根据之前的分析就比较好理解了，E(X)的含义是平均每日卖出的馒头数，而E(Y)是每个馒头之间卖出的平均时间间隔，所以两者是倒数关系：每日卖出的越多自然间隔时间越短，每日卖出的越少自然间隔时间越长。

8 小结

还有未尽的一些解释，比如：

  • 为什么指数分布常常用来描述电器寿命？
  • 为什么指数分布和几何分布一样具有无记忆性？
 
posted @ 2020-11-09 23:42  范仁义  阅读(7324)  评论(0)  编辑  收藏  举报