最大似然估计
最大似然估计
一、总结
一句话总结:
极大似然估计:就是总体的某些参数未知,通过样本取样来估计这些参数,极大就是最大,似然就是可能性,合起来就是对参数的最大可能性估计
极大似然估计中的似然 就是估计参数,比如人口身高正态分布中的 均值和标准差
1、参数估计(似然函数) 概率图(实例)?
二、最大似然估计(转)
转自:https://www.matongxue.com/madocs/447
我们假设硬币有两面,一面是“花”,一面是“字”。
一般来说,我们都觉得硬币是公平的,也就是“花”和“字”出现的概率是差不多的。
如果我扔了100次硬币,100次出现的都是“花”。
在这样的事实下,我觉得似乎硬币的参数不是公平的。你硬要说是公平的,那就是侮辱我的智商。
这种通过事实,反过来猜测硬币的情况,就是似然。
而且,我觉得最有可能的硬币的情况是,两面都是“花”:
通过事实,推断出最有可能的硬币情况,就是最大似然估计。
1 概率vs似然
让我们先来比较下概率和似然。
为了避免和我们想讨论的概率混淆,我们把硬币的“花”出现的概率称为硬币的参数。
1.1 概率
已知硬币的参数,就可以去推测抛硬币的各种情况的可能性,这称为概率。
比如已知硬币是公平的,也就是硬币的参数为0.5。
那么我们就可以推测,扔10次硬币,出现5次“花”朝上的概率为(抛硬币遵循二项分布,这个就不多解释了):
1.2 似然
正如开头所说,我们对硬币的参数并不清楚,要通过抛硬币的情况去推测硬币的参数,这称为似然。
可以再举不那么恰当(主要模型不好建立)的例子,蹭下热点。
比如我们发现,鹿晗和关晓彤戴同款手链,穿同款卫衣:
我们应该可以推测这两人关系的“参数”是“亲密”。
进一步发现,两人在同一个地方跨年:
似乎,关系的“参数”是“不简单”。
最后,关晓彤号称要把初吻留给男友,但是最近在荧幕中献出初吻,对象就是鹿晗:
我觉得最大的可能性,关系的“参数”是“在一起”。
通过证据,对两人的关系的“参数”进行推断,叫做似然,得到最可能的参数,叫做最大似然估计。
2 最大似然估计
来看看怎么进行最大似然估计。
2.1 具体的例子
我们实验的结果是,10次抛硬币,有6次是“花”。
所谓最大似然估计,就是假设硬币的参数,然后计算实验结果的概率是多少,概率越大的,那么这个假设的参数就越可能是真的。
我们先看看硬币是否是公平的,就用0.5作为硬币的参数,实验结果的概率为:
单独的一次计算没有什么意义,让我们继续往后面看。
再试试用0.6作为硬币的参数,实验结果的概率为:
之前说了,单次计算没有什么意义,但是两次计算进行比较就有意义了。
可以看到:
我们可以认为,0.6作为参数的可能性是0.5作为参数的可能性的1.2倍。
2.2 作图
我们设硬币的参数为%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) ,可以得到似然函数为:
,可以得到似然函数为:
这样我们就可以作图了:
我们可以从图中看出两点:
-
参数为0.6时,概率最大
-
参数为0.5、0.7也是有可能的,虽然可能性小一点
所以更准确的说,似然(现在可以说似然函数了)是推测参数的分布。
而求最大似然估计的问题,就变成了求似然函数的极值。在这里,极值出现在0.6。
2.3 更多的实验结果
如果实验结果是,投掷100次,出现了60次“花”呢?
似然函数为:
用0.5作为硬币的参数,实验结果的概率为:
再试试用0.6作为硬币的参数,实验结果的概率为:
此时:
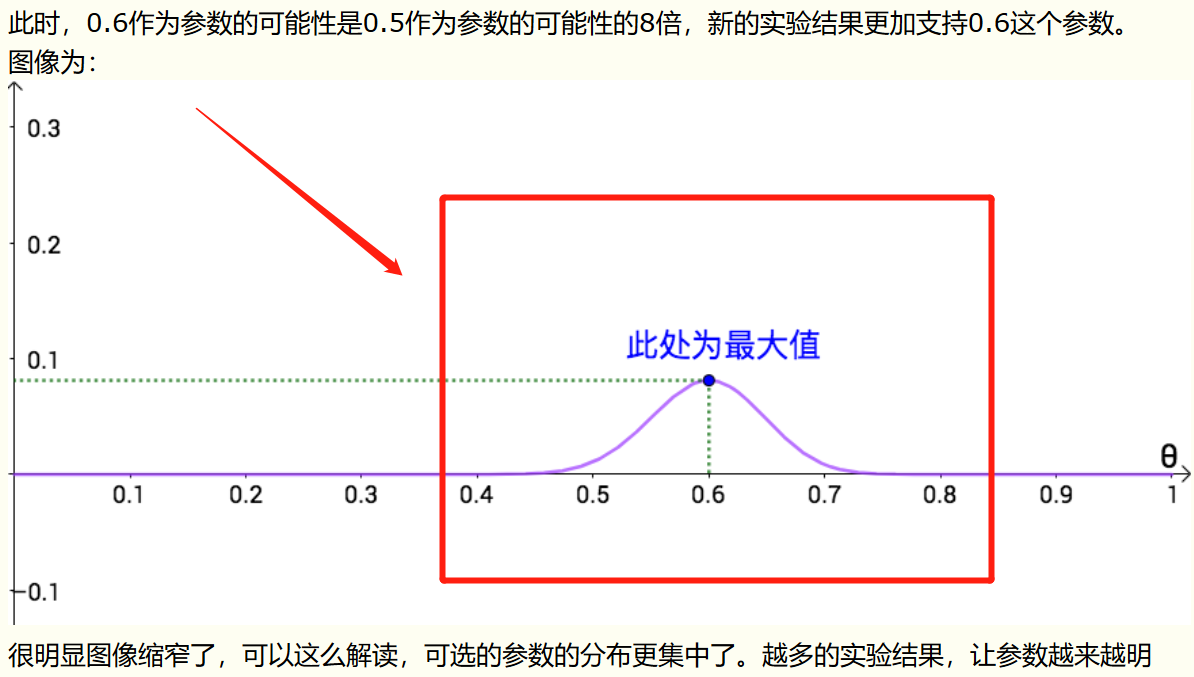
此时,0.6作为参数的可能性是0.5作为参数的可能性的8倍,新的实验结果更加支持0.6这个参数。
图像为:
很明显图像缩窄了,可以这么解读,可选的参数的分布更集中了。越多的实验结果,让参数越来越明确。
2.4 更复杂一些的最大似然估计
2.4.1 数学名词
下面提升一点难度,开始采用更多的数学名词了。
先说一下数学名词:
-
一次实验:抛硬币10次,出现6次“花”,就是一次实验。
-
二项分布:抛硬币10次,出现6次“花”的概率为0.25,出现5次“花”的概率为0.21,所有的可能的结果(比如抛硬币10次,出现11次“花”,这就是不可能)的概率,放在一起就是二项分布
2.4.2 多次实验
之前的例子只做了一次实验。只做一次实验,没有必要算这么复杂,比如投掷100次,出现了60次“花”,我直接:
不就好了?
最大似然估计真正的用途是针对多次实验。
2.4.3 上帝视角
为了说清楚这个问题,我引入一个上帝视角。
比如,我有如下的二项分布,%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 为出现“花”的概率(硬币抛10次):
为出现“花”的概率(硬币抛10次):
在实际生活中,%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 往往是不知道的,这里你可以看得到,就好像你是上帝一样。
往往是不知道的,这里你可以看得到,就好像你是上帝一样。
要提醒大家注意的一点,上面的图像只有上帝才能看到的,包括:
-
二次分布的柱状图
-
二次分布的曲线图
-
值为多少
我把只有上帝能看到的用虚线表示,%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 用淡一点的颜色表示:
用淡一点的颜色表示:
2.4.4 通过多次实验进行最大似然估计
上面的二项分布用通俗点的话来说,就是描述了抛10次硬币的结果的概率,其中,“花”出现的概率为%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 。
。
根据上面的二项分布,我进行了6次实验(也就是总共6次,每次抛10次硬币),把实验结果用点的形式标记在图像上(从技术上讲,这6个点是根据二项分布随机得到的):
这个实验结果,也就是图上的点,是我们“愚蠢的人类”可以看见的了。
可以看到,虽然进行了6次实验,但是却没有6个点,这是因为有的实验结果是一样的,就重合了。
为了方便观察,我把6个点的值用文字表示出来:
上图中的%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7B%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(500%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-34%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(1001%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(1446%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-35%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(1946%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(2391%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-35%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(2892%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(3337%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(3838%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(4283%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-37%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(4783%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(5228%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-34%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(5729%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7D%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 就是6次实验的结果,分别表示:
就是6次实验的结果,分别表示:
-
第一次实验,4次出现“花”
-
第二次实验,5次出现“花”
-
第三次实验,5次出现“花”
-
以此类推
我们用%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-msubsup%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(572%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(1026%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-msubsup%22%20transform%3D%22translate(1471%2C0)%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mn%22%20transform%3D%22translate(572%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(2497%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(2943%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-22EF%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mo%22%20transform%3D%22translate(4282%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-msubsup%22%20transform%3D%22translate(4727%2C0)%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%20transform%3D%22translate(572%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 表示每次实验结果,因为每次实验都是独立的,所以似然函数可以写作(得到这个似然函数很简单,独立事件的联合概率,直接相乘就可以得到):
表示每次实验结果,因为每次实验都是独立的,所以似然函数可以写作(得到这个似然函数很简单,独立事件的联合概率,直接相乘就可以得到):
下面这幅图,分为两部分,上面除了实验结果外,都是上帝看到的,而下面是通过实验结果,利用似然函数对%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 值的推断:
值的推断:
可以看出,推断出来的%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 值和上帝看到的差不多。之所以有差别是因为实验本身具有二项随机性,相信试验次数越多,推测会越准确。
值和上帝看到的差不多。之所以有差别是因为实验本身具有二项随机性,相信试验次数越多,推测会越准确。
自己动手试试当上帝的感觉吧,下面的%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20class%3D%22mjx-svg-mrow%22%3E%0A%3Cg%20class%3D%22mjx-svg-mi%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-3B8%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E) 滑动条可以拖动哦:
滑动条可以拖动哦:
Created with GeoGebra
最大似然估计也是机器学习的一个重要算法,大家是否通过上面的操作,是否感受到了机器是如何学习的?
3 最大似然估计与贝叶斯定理的异同
3.1 相同之处
扔了100次硬币,100次出现的都是“花”,不论是最大似然估计,或者是贝叶斯定理,都认为有必要对之前假设的硬币的参数进行调整。
我在怎样用非数学语言讲解贝叶斯定理?的最后也提出了这个问题。
3.2 不同之处
贝叶斯定理还要考虑,两面都是“花”的硬币本身存在的概率有多高。
如果我的硬币不是精心准备的,而是随机挑选的,那么一枚硬币两面都是“花”可能性微乎其微,几乎就是一个传说。
那么贝叶斯会认为哪怕扔了100次硬币,100次出现的都是“花”,但是因为两面都是“花”的硬币实在太少,那么实际这枚硬币是两面“花”的可能性仍然不高。