概率论疑难问题---1、通俗理解全概率公式和贝叶斯公式
概率论疑难问题---1、通俗理解全概率公式和贝叶斯公式
一、总结
一句话总结:
全概率就是表示达到某个目的,有多种方式,每种方式又有对应的成功率,问达到目的的概率是多少?具体做法就是把达到目的的所有情况的概率加起来就好
全概率公式:$$P ( B ) = \sum _ { i = 1 } ^ { n } P ( M _ { i } ) P ( B | M _ { i } )$$
贝叶斯公式就是当已知结果,问导致这个结果的第i原因的可能性是多少?执果索因!
贝叶斯公式:$$P ( M _ { i } | B ) = \frac { P ( M _ { i } ) P ( B | M _ { i } ) } { \sum _ { j = 1 } ^ { n } P ( M _ { j } ) P ( B | M _ { j } ) }$$
二、通俗理解全概率公式和贝叶斯公式
博客对应课程视频位置:1、全概率公式和贝叶斯公式-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/382
一、条件概率是什么
举个例子,比如让你背对着一个人,让你猜猜背后这个人是女孩的概率是多少?
直接猜测,肯定是只有50%的概率。
假如现在告诉你背后这个人是个长头发,那么女的概率就变为90%。
所以条件概率的意义就是,当给定条件发生变化后,会导致事件发生的可能性发生变化。
条件概率写法
P(A|B)表示事件B发生后事件A发生的概率,对应到上面的例中:B表示背后这个人是个长头发,A表示这个人是女孩的概率
问题:思考P(A|B)到底怎么求
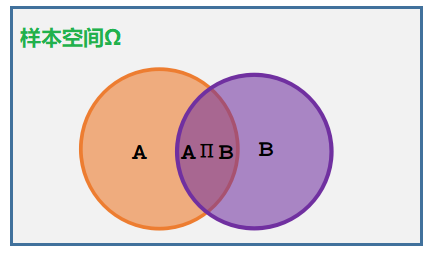
求事件A和事件B同时发生的概率
看图可得事件A和事件B同时发生的概率就是P(A∩B),也写作P(AB)
相当于P(A∩B)/1,
条件概率:事件B发生后事件A发生的概率
直接看图非常好解释
$$P(A|B)=\frac { P ( A ∩ B ) } { P ( B )}\Rightarrow p ( A \cap B ) = p ( A | B ) \times p ( B )$$条件概率和同时发生的本质区别是什么
样本空间发生了变化
条件概率:事件A发生后事件B发生的概率
$$P(B|A)=\frac { P ( B ∩ A ) } { P ( A )}\Rightarrow p ( B \cap A ) = p ( B | A ) \times p ( A )$$而P(A∩B)=P(B∩A),从图中可以轻易看出来,并且P(A∩B)和P(B∩A)都是表示事件AB同时发生的概率
所以
$$p ( A \cap B ) = p ( A | B ) \times p ( B )=p ( B \cap A ) = p ( B | A ) \times p ( A )$$也就是
$$p ( A | B ) \times p ( B ) = p ( B | A ) \times p ( A )$$再变换一下
$$p ( A | B ) = \frac { P ( B | A ) \times p ( A ) } { P ( B )}$$二、全概率公式
最近《斗罗大陆》的动画不是在热播么,所以拿《斗罗大陆》来举例子
假设唐三面前有一个敌人比比东,唐三有三种单独的方式可以打败比比东,方式一是使用蓝银皇武魂,方式二是使用昊天锤武魂,方式三使用唐门暗器(比如佛怒唐莲),唐三使用这三种招式的概率分别是:
Mi表示唐三单独选择某种招式,比如P(M1)表示唐三选择蓝银皇武魂概率,P(Hi)表示唐三第i种招式命中的概率,
P(M1)=0.5,P(M2)=0.4,P(M3)=0.1
这三种招式成功让比比东中招(中招就算打败)的概率分别为:
P(H1)=0.3,P(H2)=0.2,P(H3)=0.5
求唐三打败比比东的概率是多少?

解决思路:
这里唐三有三种方式打败比比东,我们把这三种方式打败比比东的概率加起来,就是总的打败比比东的概率
P(B)表示唐三打败比比东的概率
$$P(B)=P(M1) \times P(B|M1)+P(M2) \times P(B|M2)+P(M3) \times P(B|M3)$$这一步有问题
$$P(B)=P(M1) \times P(H1)+P(M2) \times P(H2)+P(M3) \times P(H3)$$$$P(B)=0.5 \times 0.3+0.4 \times 0.2+0.1 \times 0.5=0.15+0.08+0.05=0.28$$
全概率就是表示达到某个目的,有多种方式,每种方式又有对应的成功率,问达到目的的概率是多少?
具体做法就是把达到目的的所有情况的概率加起来就好
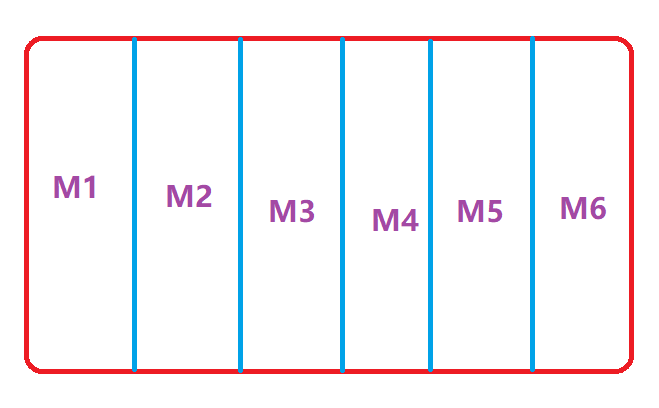
全概率公式描述
公式表示若事件M1,M2,…,Mn构成一个完备事件组且都有正概率,则对任意一个事件B都有公式成立。
完备事件组
三、贝叶斯公式
我们照样来说唐三VS比比东的问题,前面的描述一样,
我们现在已知 唐三打败了比比东,
现在的问题是 上述三种方式中,唐三使用哪种方式的可能性最大
解决这个问题的方式也很简单,
就是把使用这三种方式打败比比东的概率分别求出来,然后比较一下就好了
这些前面已经算过了的
使用第一种方式打败比比东的概率
$$p ( M1 | B ) = \frac { P(B|M1) \times P(M1) } { P ( B )}=\frac { 0.3 \times 0.5 } { 0.28}≈0.536$$使用第二种方式打败比比东的概率
$$p ( M2 | B ) = \frac { P(B|M2) \times P(M2) } { P ( B )}=\frac { 0.2 \times 0.4 } { 0.28}≈0.286$$使用第三种方式打败比比东的概率
$$p ( M3 | B ) = \frac { P(B|M3) \times P(M3) } { P ( B )}=\frac { 0.5 \times 0.1 } { 0.28}≈0.178$$从上面的结果中可以看到使用第一种方式的概率最大
贝叶斯公式
贝叶斯公式就是当已知结果,问导致这个结果的第i原因的可能性是多少?执果索因!
系列课程视频位置:
1、全概率公式和贝叶斯公式-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/382
2、通俗理解泊松分布-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/385
3、通俗理解协方差与相关系数-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/386
4、通俗理解概率论中的“矩”-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/387
5、通俗理解中心极限定理-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/388
6、极大似然估计-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/389
7、通俗理解最小二乘法-范仁义-读书编程笔记
https://www.fanrenyi.com/video/45/390




