宋浩《概率论与数理统计》笔记---4.3.1、 常见离散型的期望与方差
宋浩《概率论与数理统计》笔记---4.3.1、 常见离散型的期望与方差
一、总结
一句话总结:
0-1分布:EX=p;DX=pq
二项分布:EX=np;DX=npq:就相当于是n个0-1分布
几何分布:EX=1/p;DX=(1-p)/p^2
泊松分布:EX=λ;DX=λ
1、0-1分布的期望和方差?
0-1分布:EX=p;DX=pq
2、二项分布的期望和方差?
EX=np,推导过程稍麻烦,后面求和部分是(p+q)^(n-1)次方,所以是1
二项分布的方差:DX=npq
下面那张图,0-1分布也可以解释二项分布的期望和方差
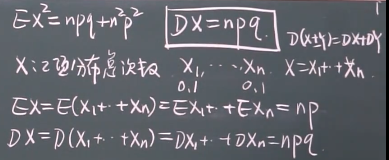
3、如果一个式子直接不好求,可以换个思路,先求积分再求导?
先求积分后求导后,这样就可以转化为等比数列的和(x/(1-x)),这样求导也很方便
4、几何分布的期望和方差?
几何分布期望:EX=1/p
几何分布方差:DX=(1-p)/p^2
5、泊松分布期望和方差?
泊松分布期望:EX=λ:倒数第二步是转化为一个泊松分布,那么包含所有概率,结果自然是1,所以最后的结果是λ
泊松分布方差:DX=λ
二、内容在总结中
博客对应课程的视频位置:
版权申明:欢迎转载,但请注明出处
一些博文中有一些参考内容因时间久远找不到来源了没有注明,如果侵权请联系我删除。
在校每年国奖、每年专业第一,加拿大留学,先后工作于华东师范大学和香港教育大学。
2025-04-30:宅加太忙,特此在网上找女朋友,坐标上海,非诚勿扰,vx:fan404006308
AI交流资料群:753014672




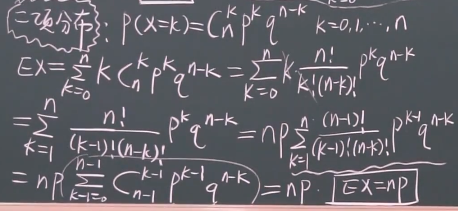


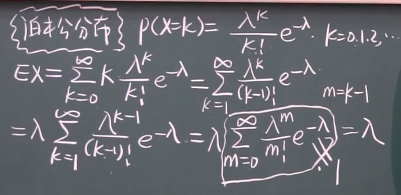

 浙公网安备 33010602011771号
浙公网安备 33010602011771号