指数分布与泊松分布

指数分布与泊松分布

一、总结

一句话总结：

泊松分布：$$P(X = k) = e^{-\lambda}\displaystyle\frac{\lambda^k}{k!}, \ k = 0, 1, 2,..., $$

指数分布：$$f(x) = \begin{cases} \lambda e^{-\lambda x}, \quad x > 0 \\ 0, \quad \quad \quad x \leq 0 \end{cases} $$

 

 

二、指数分布与泊松分布的关系（转）

转自或参考：https://www.cnblogs.com/fanlumaster/p/13766064.html

 

 

泊松分布的定义

设随机变量 X 所有可能取的值为 0 , 1, 2, ... , 且取各个值的概率为：

 

\[P(X = k) = e^{-\lambda}\displaystyle\frac{\lambda^k}{k!}, \ k = 0, 1, 2,..., \]

 

其中，\(\lambda > 0\) 是常数，则称 X 服从参数为 \(\lambda\) 的泊松分布，记作 \(X \sim P(\lambda)\).

指数分布的定义

若连续型随机变量 X 的概率密度为:

 

\[f(x) = \begin{cases} \lambda e^{-\lambda x}, \quad x > 0 \\ 0, \quad \quad \quad x \leq 0 \end{cases} \]

 

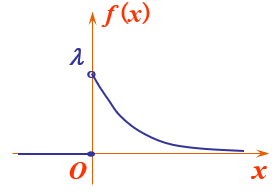
其中 \(\lambda > 0\) 为常数，则称 X 服从参数 \(\lambda\) 的指数分布，记为 \(X \sim E(\lambda)\).

指数分布的函数：

 

\[F(x) = \begin{cases} 1 - e^{-\lambda x}, \quad x > 0 \\ 0, \quad \quad \quad \quad x \leq 0 \end{cases} \]

 

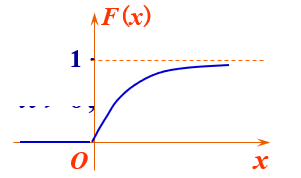
指数分布与泊松流的关系

在泊松流中，记时间间隔 \((0, t]\) 中出现的质点数为 X

则 \(X \sim P(\lambda t)\)，即有：

 

\[P \{ X = k \} = \displaystyle\frac{{(\lambda t)}^k}{k!} e^{- \lambda t}, \ k = 0,1,2,... \]

 

其中参数 \(\lambda\) 称为泊松强度.

记 \(T\) 表示第一个质点出现的时间，则 ${ T > t } \Leftrightarrow $ 在 \((0, t]\) 内没有粒子到达 \(P \{ T > t \} = P \{ X = 0 \} = e^{- \lambda t}\)，即 \(T\) 的分布函数为

 

\[F(t) = P \{T \leq t \} = 1 - e^{- \lambda t} \quad (t > 0) \]

 

 

\[\therefore Y \sim E(\lambda) \]

 

注：上面的泊松流指的应该（不确定）是泊松过程：