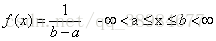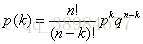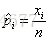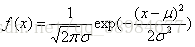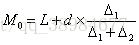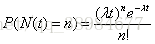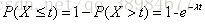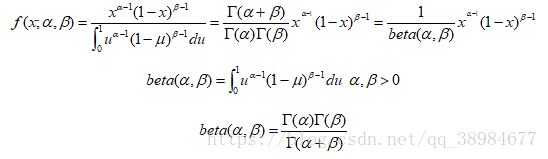随机变量概率分布函数汇总
随机变量概率分布函数汇总
一、总结
一句话总结:
概率分布用以表达随机变量取值的概率规律,根据随机变量所属类型的不同,概率分布取不同的表现形式
离散型分布:二项分布、多项分布、伯努利分布、泊松分布
连续型分布:均匀分布、正态分布、指数分布、伽玛分布、偏态分布、贝塔分布
1、伯努利分布?
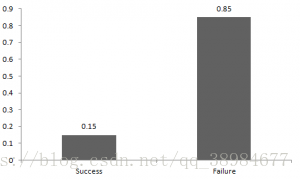
【成功和失败的概率不一定相等】:伯努利分布只有两种可能的结果,1-成功和0-失败,具有伯努利分布特征的随机变量X可以取值为1的概率为p,取值为0的概率1-p,其中成功和失败的概率不一定相等
2、均匀分布?
【均匀分布所有可能结果的n个数的发生概率是相等的】:均匀分布变量X的概率密度函数([概率密度函数]概念是针对连续分布的,求积分即发生概率)为
3、伯努利分布和二项分布的关系?
1、【伯努利分布是二项分布的单次试验的特例】,即单次二项分布试验
2、二项分布和伯努利分布的每次试验都【只有两个可能的结果】
3、二项分布每次试验都是互相独立的,【每一次试验都可以看作一个伯努利分布】
4、泊松分布?
【大量事件是有固定频率的】。特点:可以预估这些事件的总数,但是没法知道具体的发生时间和发生地点。已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?
【泊松分布即描述某段时间内,事件具体的发生频率】
5、泊松分布的主要特点?
【计数过程】:泊松分布是个计数过程,通常用于模拟一个非连续事件在连续时间中的发生次数
【成功事件互不影响】:任何一个成功事件不能影响其它的成功事件(N(t+s)-N(t)增量之间互相独立)
【长短时间成功概率相等】:经过短时间间隔的成功概率必须等于经过长时间间隔的成功概率
【无穷小时成功概率趋近零】:时间间隔趋向于无穷小的时候,一个时间间隔内的成功概率趋近零
6、指数分布?
【指数分布是事件的时间间隔的概率】。例如婴儿出生的时间间隔、来电的时间间隔、奶粉销售的时间间隔、网站访问的时间间隔
【指数分布的公式可以从泊松分布推断出来】。
7、正态分布和二项分布的关系&正态分布和泊松分布的关系?
以下条件下,【正态分布是二项分布的一种极限形式】:1.试验次数非常大或者趋近无穷,即n→∞;2.p和q都不是无穷小
参数λ→∞的时候,【正态分布是泊松分布的极限形式】
指数分布和泊松分布的关系:如果随机事件的时间间隔服从参数为λ的指数分布,那么在时间周期t内事件发生的总次数服从泊松分布,相应的参数为λt
8、以下条件下,泊松分布是二项分布的极限形式?
1.试验次数非常大或者趋近无穷,即n→∞;
2.每次试验的成功概率相同且趋近零,即p→0;
3.np=λ是有限值
二、随机变量概率分布函数汇总-离散型分布+连续型分布(转)
转自:随机变量概率分布函数汇总-离散型分布+连续型分布
https://blog.csdn.net/kwame211/article/details/81167082
概率分布用以表达随机变量取值的概率规律,根据随机变量所属类型的不同,概率分布取不同的表现形式
离散型分布:二项分布、多项分布、伯努利分布、泊松分布
连续型分布:均匀分布、正态分布、指数分布、伽玛分布、偏态分布、贝塔分布
一.伯努利分布
伯努利分布只有两种可能的结果,1-成功和0-失败,具有伯努利分布特征的随机变量X可以取值为1的概率为p,取值为0的概率1-p,其中成功和失败的概率不一定相等
成功的概率=0.15,失败的概率=0.85,来自伯努利分布的随机变量X的期望值如为:E(X)=1*p+0*(1-p)=p;随机变量与二项分布的方差为:V(X)=E(X²)–[E(X)]² =p–p²
二.均匀分布
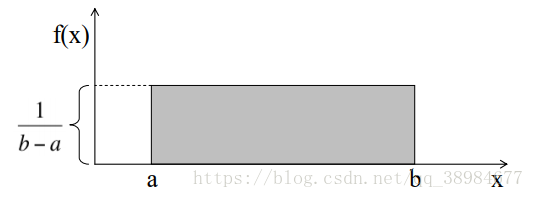
均匀分布所有可能结果的n个数的发生概率是相等的,均匀分布变量X的概率密度函数([概率密度函数]概念是针对连续分布的,求积分即发生概率)为:
均匀分布密度函数曲线的形状是一个矩形,这也是均匀分布又称为矩形分布的原因,a和b是参数。例子:花店每天销售的花束数量是均匀分布的,最多为40,最少为10,计算日销售量在15到30之间的概率(即密度函数曲线下的面积):(30-15)*(1/(40-10))=0.5。遵循均匀分布的变量X的期望和方差为:(a+b)/2、(b-a)^2/12
三.二项分布
二项分布的每一次尝试都是独立的,前一次投掷的结果不能决定或影响当前投掷的结果,只有两个可能结果并且重复n次的实验叫做二项式。二项分布的参数是n和p,其中n是试验的总数,p是每次试验成功的概率。n次独立重复事件发生k次的概率为:
均值和方差:np、npq
-
#R对应的函数形式,其他分布的函数同理 -
dbinom(x, size, prob) #每个点对应的概率密度值(即发生概率值) -
pbinom(x, size, prob) #事件的累计概率值 -
qbinom(p, size, prob) #给出累计值(与p概率值匹配)的数字 -
rbinom(n, size, prob) #从样本产生概率生成所需数量的概率值
四.多项分布
多项分布是二项分布的推广扩展,在n次独立实验中每次只输出k种结果中的一个,且每种结果都有一个确定概率,多项分布给出在多种输出状态的情况下,关于成功次数的各种组合的概率
举个例子,投掷n次骰子,这个骰子共有6种结果输出,且1点出现概率为p1,2点出现概率p2,…多项分布给出了在n次试验中,骰子1点出现x1次,2点出现x2次,3点出现x3次,…,6点出现x6次。这个结果组合的概率公式为:
xi为第i种状态输出结果的频度,根据多项分布的极大似然估计得
五.正态分布
正态分布的特征:1.分布的平均值、中位数和模式一致;2.分布曲线是钟形的,关于线x=μ对称;3.曲线下的总面积为1;4.两个正态分布之积仍为正态分布;5.两个独立且服从正态分布的随机变量的和服从正态分布
若随机变量X服从位置参数尺度参数
的概率分布(N(
,
)),且其概率密度函数为:
正态曲线下横轴上一定区间的面积反映该区间的例数占总例数的百分比,或变量值落在该区间的概率
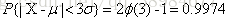
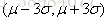
法则)
六.偏态分布
偏态分布(特点是左右不对称,频数分布的高峰位于一侧,尾部向另一侧延伸)与正态分布相对,是连续随机变量概率分布的一种,可通过峰度和偏度的计算,衡量偏态程度
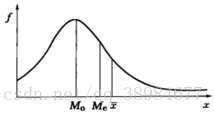
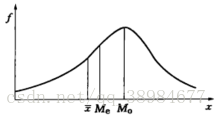
正偏态分布(右偏分布):M>Me>Mo(平均数>中位数>众数)
负偏态分布(左偏分布):M<Me<Mo(平均数<中位数<众数)
分组下的众数(均值大于众数为右偏分布,均值小于众数为左偏分布):在组距分组的情况下,众数计算需考虑最大频数所在组相邻组的情况
L最大频数所在组的下限值,d为最大频数所在组的组距,为最大频数所在组频数与上组频数之差,
为最大频数所在组频数与下组频数之差
七.泊松分布
大量事件是有固定频率的。特点:可以预估这些事件的总数,但是没法知道具体的发生时间和发生地点。已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?
泊松分布的主要特点:
泊松分布是个计数过程,通常用于模拟一个非连续事件在连续时间中的发生次数
1.任何一个成功事件不能影响其它的成功事件(N(t+s)-N(t)增量之间互相独立)
2.经过短时间间隔的成功概率必须等于经过长时间间隔的成功概率
3.时间间隔趋向于无穷小的时候,一个时间间隔内的成功概率趋近零
泊松分布即描述某段时间内,事件具体的发生频率。泊松分布的概率分布函数公式如下所示
等号左边P表示概率,N表示某种函数关系,t表示时间,n表示数量,1小时内出生3个婴儿的概率,就表示为 P(N(1)=3)等号的右边,λ表示事件的频率(如平均每小时出生3个)
表示长度为t的时间间隔中的平均事件数(
为事件的发生率),泊松分布的均值和方差均为
八.指数分布
指数分布是事件的时间间隔的概率。例如婴儿出生的时间间隔、来电的时间间隔、奶粉销售的时间间隔、网站访问的时间间隔
指数分布的公式可以从泊松分布推断出来。如果下一个婴儿出生要间隔时间t,就等同于t之内没有任何婴儿出生
反过来,事件在时间t之内发生的概率,就是1减去上面的值
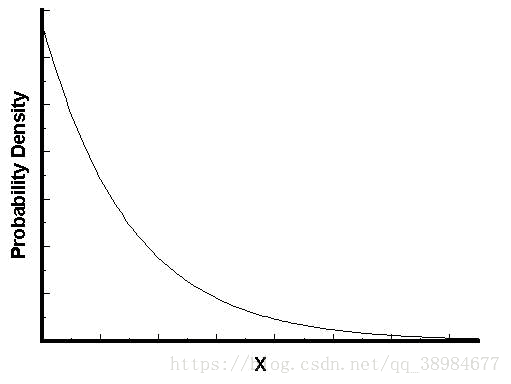
指数分布的图形大体如下:随着间隔时间变长,时间的发生概率急剧下降,呈现指数式衰减
九.伽玛分布
Gamma分布即多个独立且相同分布的指数分布变量和的分布,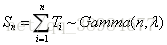
十.贝塔分布
贝塔分布可以看作是一个描述概率p(定义在区间(0,1))的连续概率分布,当不知道某个具体事件的发生概率时,贝塔分布可以给出所有概率出现的可能性大小
具体实例帮助理解概念:棒球击球率(batting average)-用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。现在有一个棒球运动员,希望能预测他在这一赛季中的棒球击球率是多少,但是如果这个棒球运动员只打了一次且命中,那么击球率是100%,这显然是不合理的,因为根据棒球的历史信息知道这个击球率应该是0.215到0.36之间才对。对于这个问题,可以用一个二项分布表示(一系列成功或失败),一个最好的方法来表示这些经验(即先验信息)就是用beta分布,表示在没有看到这个运动员打球之前就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的
将这些先验信息转换为beta分布的参数,知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取α=81,β=219
之所以取这两个参数是因为:
beta分布的期望均值是α/(α+β)=81/(81+219)=0.27
从图中可以看到这个分布主要落在了(0.2,0.35)间,这是从经验中得出的合理的范围
beta分布的概率密度函数(体现了beta分布与gamma分布的关系)
有了先验信息,现在考虑运动员只打一次球,那么他现在的数据就是”1中1击”。这时候就可以更新分布了,让这个曲线做一些移动去适应新信息。beta分布在数学上就给我们提供了这一性质,他与二项分布是共轭先验。所谓共轭先验就是先验分布是beta分布,而后验分布同样是beta分布。结果很简单:
beta(a+hits,b+misses)
其中a和b是一开始的参数,在这里是81和219。在这一例子里a增加了1(击中了一次)。β没有增加(没有漏球)。这就是新的beta分布Beta(81+1,219),beta分布的概率密度函数曲线可能会变得更加陡峭或平稳
十一.狄利克雷分布
狄利克雷分布是beta分布在多项情况下的推广,也是多项分布的共轭先验分布,狄利克雷分布的概率密度函数如下
十二.共轭先验分布
共轭是选取一个函数作为似然函数的先验概率分布,使得后验分布函数和先验分布函数形式一致(Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布)
贝叶斯规则:后验分布=似然函数*先验概率分布
十三.分布之间的关系
伯努利分布和二项分布的关系:
1.伯努利分布是二项分布的单次试验的特例,即单次二项分布试验
2.二项分布和伯努利分布的每次试验都只有两个可能的结果
3.二项分布每次试验都是互相独立的,每一次试验都可以看作一个伯努利分布
泊松分布和二项分布的关系:
以下条件下,泊松分布是二项分布的极限形式:
1.试验次数非常大或者趋近无穷,即n→∞;
2.每次试验的成功概率相同且趋近零,即p→0;
3.np=λ是有限值
正态分布和二项分布的关系&正态分布和泊松分布的关系:
以下条件下,正态分布是二项分布的一种极限形式:
1.试验次数非常大或者趋近无穷,即n→∞;
2.p和q都不是无穷小
参数λ→∞的时候,正态分布是泊松分布的极限形式
指数分布和泊松分布的关系:
如果随机事件的时间间隔服从参数为λ的指数分布,那么在时间周期t内事件发生的总次数服从泊松分布,相应的参数为λt