用 Python 检验数据正态分布的几种方法
用 Python 检验数据正态分布的几种方法
一、总结
一句话总结：
scipy.stats.anderson(x, dist ='norm' ) 该方法是由 scipy.stats.kstest 改进而来的，可以做正态分布、指数分布、Logistic 分布、Gumbel 分布等多种分布检验。
scipy.stats.normaltest(a,axis=0) 该方法专门用来检验数据是否为正态性分布
二、用 Python 检验数据正态分布的几种方法
转自或参考：用 Python 检验数据正态分布的几种方法
https://zhuanlan.zhihu.com/p/40447523
什么是正态分布
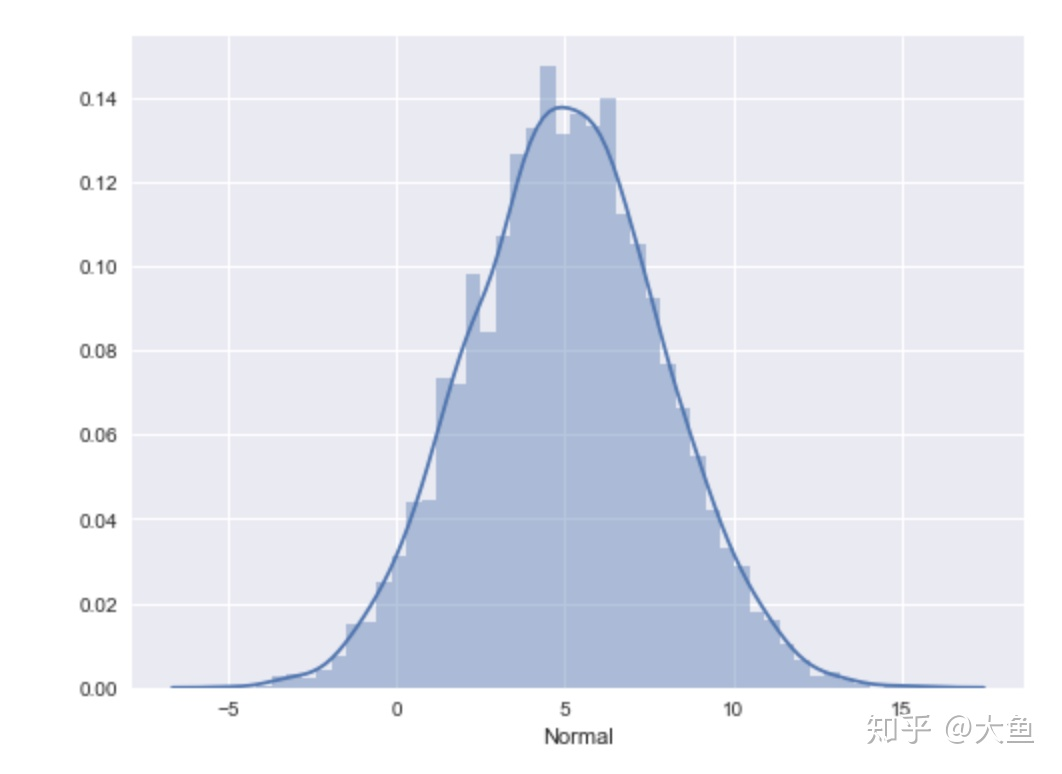
关于什么是正态分布，早在中学时老师就讲过了。通俗来讲，就是当我们把数据绘制成频率直方图，所构成曲线的波峰位于中间，两边对称，并且随着往两侧延伸逐渐呈下降趋势，这样的曲线就可以说是符合数学上的正态分布。由于任何特征的频率总和都为100%或1，所以该曲线和横轴之间部分的面积也为100%或1，这是正态分布的几何意义。
如下图，是数据统计实例中出现的正态分布性数据：
为什么要做正态性检验
对此我的理解是，正态性可以保证随机性，因为随机数就是正态分布的，这里可以用高尔顿板来形象化地理解：
高尔顿板为一块竖直放置的板，上面有交错排列的钉子。让小球从板的上端自由下落，当其碰到钉子后会随机向左或向右落下。最终，小球会落至板底端的某一格子中。假设板上共有 n 排钉子，每个小球撞击钉子后向右落下的概率为（当左、右概率相同时
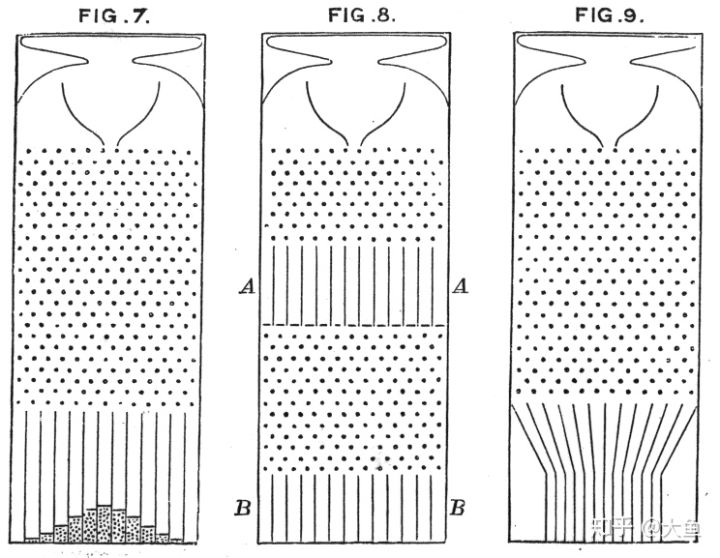
高尔顿绘制的高尔顿板示意图
高尔顿板是多个二次分布的累加，是离散的，但如果是无数次进行累加，那么它的极限状态就是一个钟形曲线的正态分布。举个通俗的例子，如果统计全国成年女性的身高，那么结果曲线的波峰大概率落在 160-165cm 这个范围内，然后左侧对应偏低数据与右侧对应的偏高数据，占据比例极小，如果收集的数据足够多又保证随机，那么最后的曲线就应该近似正态分布。
因此许多统计方法都是以正态分布为基础的，如方差分析、相关和回归分析等等。也有许多统计方法虽然不要求必须服从正态分布，但具有统计意义的数据量在极大的时候，是接近正态分布的，所以针对其使用的统计方法依然是以正态分布为理论基础进行改进的。
用 Python 如何检验正态性
方法：scipy.stats.shapiro(x)
官方文档：SciPy v1.1.0 Reference Guide
参数：x - 待检验数据
返回：W - 统计数；p-value - p值
2. scipy.stats.kstest
方法：scipy.stats.kstest (rvs, cdf, args = ( ), N = 20, alternative ='two-sided', mode ='approx')
官方文档：SciPy v0.14.0 Reference Guide
参数：rvs - 待检验数据，可以是字符串、数组；
cdf - 需要设置的检验，这里设置为 norm，也就是正态性检验；
alternative - 设置单双尾检验，默认为 two-sided
返回：W - 统计数；p-value - p值
方法：scipy.stats.anderson (x, dist ='norm' )
该方法是由 scipy.stats.kstest 改进而来的，可以做正态分布、指数分布、Logistic 分布、Gumbel 分布等多种分布检验。默认参数为 norm，即正态性检验。
官方文档：SciPy v1.1.0 Reference Guide
参数：x - 待检验数据；dist - 设置需要检验的分布类型
返回：statistic - 统计数；critical_values - 评判值；significance_level - 显著性水平
4. scipy.stats.normaltest
方法：scipy.stats.normaltest (a, axis=0)
该方法专门用来检验数据是否为正态性分布，官方文档的描述为：
Tests whether a sample differs from a normal distribution.
This function tests the null hypothesis that a sample comes from a normal distribution. It is based on D’Agostino and Pearson’s [R251], [R252] test that combines skew and kurtosis to produce an omnibus test of normality.
官方文档：SciPy v0.14.0 Reference Guide
参数：a - 待检验数据；axis - 可设置为整数或置空，如果设置为 none，则待检验数据被当作单独的数据集来进行检验。该值默认为 0，即从 0 轴开始逐行进行检验。
返回：k2 - s^2 + k^2，s 为 skewtest 返回的 z-score，k 为 kurtosistest 返回的 z-score，即标准化值；p-value - p值
