算法与数据结构---6.8、斐波那契数列-矩阵快速幂

算法与数据结构---6.8、斐波那契数列-矩阵快速幂

一、总结

一句话总结：

斐波那契数列的矩阵快速幂的解法，也就是将递推表达式化成矩阵的幂操作和乘法操作，利用快速幂，可以得到O(logn)的解法

#include <iostream>
#include <cstring>
using namespace std;
const int mod=1000000007;

//定义矩阵对应的结构体
struct Matrix{
    int row,column;
    long long v[3][3];
    Matrix(){
        memset(v,0,sizeof(v));
    }
};

//矩阵乘法
Matrix multiply(Matrix a,Matrix b){
    Matrix ans;
    ans.row=a.row;
    ans.column=b.column;
    //具体来做矩阵乘法
    for(int i=1;i<=a.row;i++){
        for(int j=1;j<=b.column;j++){
            for(int k=1;k<=a.column;k++){
                ans.v[i][j]+=(a.v[i][k]*b.v[k][j])%mod;
                ans.v[i][j]%=mod;
            }
        }
    }
    return ans;
}


//矩阵的快速幂
Matrix pow(Matrix a,long long n){
    Matrix ans,base=a;
    ans.row=2;ans.column=2;
    ans.v[1][1]=ans.v[2][2]=1;
    while(n){
        if(n%2==1) ans=multiply(ans,base);
        base=multiply(base,base);
        n/=2;
    }
    return ans;
}


int main(){
    long long n;
    cin>>n;
    Matrix ans,base,last;
    //初始化base矩阵
    base.row=2;base.column=2;
    base.v[1][1]=base.v[1][2]=base.v[2][1]=1;
    //初始化last矩阵
    last.row=2;last.column=1;
    last.v[1][1]=last.v[2][1]=1;
    if(n==1||n==2){
        cout<<1<<endl;
    }else{
        ans=pow(base,n-2);
        ans=multiply(ans,last);
        cout<<ans.v[1][1]<<endl;
    }

    return 0;
}

 

 

1、斐波那契数列-矩阵快速幂前置知识：矩阵乘法？

矩阵阵法就是按照矩阵相乘的规律，一步步来做的，也就是拿矩阵a的每一行乘以矩阵b的每一列，并且把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘

Matrix multiply(Matrix a,Matrix b){
    Matrix ans;
    ans.row=a.row;
    ans.column=b.column;
    //遍历矩阵a的每一行
    for(int i=1;i<=a.row;i++){
        //遍历矩阵b的每一列
        for(int j=1;j<=b.column;j++){
            //把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘
            for(int k=1;k<=a.column;k++){
                ans.v[i][j]+=a.v[i][k]*b.v[k][j];
            }
        }
    }
    return ans;
}

 

 

2、斐波那契数列-矩阵快速幂前置知识：快速幂？

比如在求a^11的时候，快速幂就是利用11的二进制1011，也即11=2º×1+2¹×1+2²×0+2³×1=1+2+8，将a^11转化为a^1*a^2*a^8，从而用O(logn)的时间复杂度求解

#include <iostream>
using namespace std;

int pow(int a,int n){
   int ans=1,base=a;
   while(n){
       if(n%2==1) ans=ans*base;
       base=base*base;
       n=n/2;
   }
   return ans;
}

int main(){
    cout<<pow(2,22)<<endl;
    return 0;
}

 

 

 

 

二、斐波那契数列

博客对应课程的视频位置：6.8、斐波那契数列-矩阵快速幂
https://www.fanrenyi.com/video/27/282

 

1、前置知识：矩阵乘法

/*

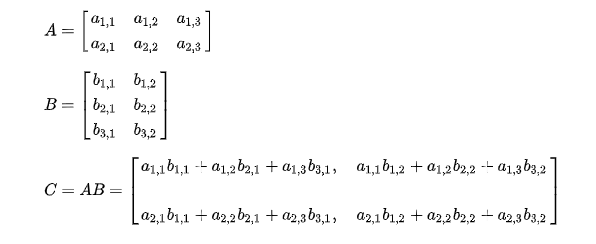
矩阵的乘法在算法中有很多应用，
比如直接考矩阵的乘法，比如用矩阵优化递推表达式等等


矩阵a*矩阵b 要满足矩阵a的列等于矩阵b的行
最后乘出来的矩阵的行为矩阵a的行
列为矩阵b的列

总结：
矩阵阵法就是按照矩阵相乘的规律，一步步来做的
也就是拿矩阵a的每一行乘以矩阵b的每一列，
并且把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘


矩阵a
1 2 3 
4 5 6

矩阵b
1 2
3 4
5 6


1*1+2*3+3*5

*/

#include <iostream>
#include <cstring>
using namespace std;

struct Matrix{
    int row,column;
    int v[5][5];
    Matrix(){
        memset(v,0,sizeof(v));
    }
};

Matrix multiply(Matrix a,Matrix b){
    Matrix ans;
    ans.row=a.row;
    ans.column=b.column;
    //遍历矩阵a的每一行
    for(int i=1;i<=a.row;i++){
        //遍历矩阵b的每一列
        for(int j=1;j<=b.column;j++){
            //把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘
            for(int k=1;k<=a.column;k++){
                ans.v[i][j]+=a.v[i][k]*b.v[k][j];
            }
        }
    }
    return ans;
}

int main(){
    Matrix a,b,ans;
    a.row=2;a.column=3;
    b.row=3;b.column=2;

    a.v[1][1]=1;a.v[1][2]=2;a.v[1][3]=3;
    a.v[2][1]=4;a.v[2][2]=5;a.v[2][3]=6;

    b.v[1][1]=1;b.v[1][2]=2;
    b.v[2][1]=3;b.v[2][2]=4;
    b.v[3][1]=5;b.v[3][2]=6;

    ans=multiply(a,b);

    cout<<ans.v[1][1]<<endl;

    return 0;
}

 

 

2、前置知识：快速幂

/*

快速幂：

首先，快速幂的目的就是做到快速求幂，

假设我们要求a^n，那么其实n是可以拆成二进制的，
例如当n==11时
11的二进制是1011，
11 =2º×1+2¹×1+2²×0+2³×1=1+2+8，
所以
a^11=a^1*a^2*a^8
原来算11次，现在只需要算三次

具体怎么算呢：
我们可以用一个变量base来在每次循环的时候记录a^i，
最开始base是a
然后每次循环让base=base*base
那么base的值
a-->a^2-->a^4-->a^8-->a^16-->a^32.......
然后根据11的二进制，1011，
取位为1时候的base值即可，
也就是取a，a^2，a^8

由此可以得到代码：


*/

#include <iostream>
using namespace std;

int pow(int a,int n){
   int ans=1,base=a;
   while(n){
       if(n%2==1) ans=ans*base;
       base=base*base;
       n=n/2;
   }
   return ans;
}

int main(){
    cout<<pow(2,22)<<endl;
    return 0;
}

 

 

 

3、矩阵快速幂

我们来看这样一个式子

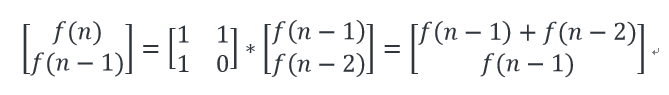
可以一路传递到出口f(2)、f(1)

所以我们可以求出

 

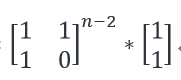
这样得到的结果就是

 

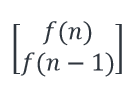
所以我们在这个结果取到f(n)就是所求的解

而求幂可以采用快速幂解法把

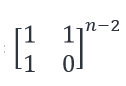
时间复杂度降为logn

/*


注意点：
1、
读入n的时候不能用int，因为1<=n<2^63

2、
注意结构体中的数组要用 long long类型，因为涉及到矩阵的乘法，
涉及到两个数相乘，所以int mod 1000000007之后，两个数相乘，还是会超int

3、
因为读入的n是long long类型，所以函数传递参数的时候，也要记得别用成int了


*/
#include <iostream>
#include <cstring>
using namespace std;
const int mod=1000000007;

//定义矩阵对应的结构体
struct Matrix{
    int row,column;
    long long v[3][3];
    Matrix(){
        memset(v,0,sizeof(v));
    }
};

//矩阵乘法
Matrix multiply(Matrix a,Matrix b){
    Matrix ans;
    ans.row=a.row;
    ans.column=b.column;
    //具体来做矩阵乘法
    for(int i=1;i<=a.row;i++){
        for(int j=1;j<=b.column;j++){
            for(int k=1;k<=a.column;k++){
                ans.v[i][j]+=(a.v[i][k]*b.v[k][j])%mod;
                ans.v[i][j]%=mod;
            }
        }
    }
    return ans;
}


//矩阵的快速幂
Matrix pow(Matrix a,long long n){
    Matrix ans,base=a;
    ans.row=2;ans.column=2;
    ans.v[1][1]=ans.v[2][2]=1;
    while(n){
        if(n%2==1) ans=multiply(ans,base);
        base=multiply(base,base);
        n/=2;
    }
    return ans;
}


int main(){
    long long n;
    cin>>n;
    Matrix ans,base,last;
    //初始化base矩阵
    base.row=2;base.column=2;
    base.v[1][1]=base.v[1][2]=base.v[2][1]=1;
    //初始化last矩阵
    last.row=2;last.column=1;
    last.v[1][1]=last.v[2][1]=1;
    if(n==1||n==2){
        cout<<1<<endl;
    }else{
        ans=pow(base,n-2);
        ans=multiply(ans,last);
        cout<<ans.v[1][1]<<endl;
    }

    return 0;
}