Jumping Monkey 2021CCPC网络赛重赛1011

题目链接：https://acm.hdu.edu.cn/showproblem.php?pid=7136

题意：

　　给一颗n个点的树，每个点标记为1到n，每个点有自己的权值ai（保证不一样）。有只猴子可以从u点跳到v点，当且仅当u点到v点的最短路径上权值最大的点是v点。问猴子从k点开始（k∈【1.n】）最大可以跳多少个点。对于样例二，猴子在点1时，它可以跳 1 -> 3 -> 2 -> 4 共4个点。

 

思路：

　　第一眼看过去就想到换根DP，推了半天不会转移，然后想着从最大值开始dfs维护单调栈，发现还是搞不了，太菜了QAQ　　

　　考虑最大权值的点，显然该连通块的每个点都可以跳到该点，该点对该连通块内所有点的贡献为1（所有点都可以跳到该点上）

　　然后考虑次大权值的点，如果某个点到次大权值点的最短路径上有最大值，显然那个点无法到达次大值点，所以我们干脆把该连通块最大值点的所有连边都砍了，分成若干了连通块，每个连通块都有自己的最大值，这样就可以去求别的连通块对答案的贡献，不断重复这个过程就可以维护出每个点的最终答案。如图：（红色数字表示该点能跳多少步，黑色数字表示节点权值）

　 

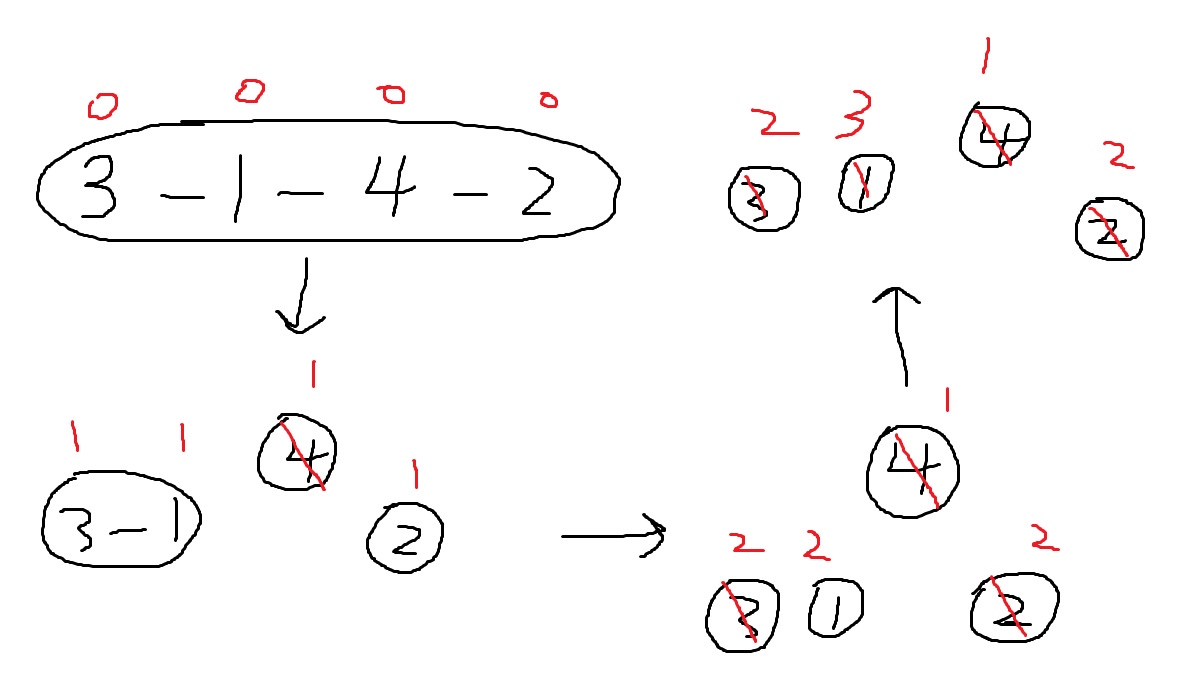
　　这个递归过程不好实现，所以我们考虑反过来进行这个过程。

　　按权值从小到大枚举点u，首先把点u单独放入一个连通块（区分一下没遍历到的点），然后遍历它的相邻节点，如果有相邻节点在另一个连通块内，那么说明另一个连通块是因为点u砍断了点u的出边而产生的（因为权值从小到大枚举，当前的权值比枚举过的权值大），把他们重新合成一个连通块，其中点u作为父节点，另一个连通块的根作为子节点，这就有点像并查集存在一个上下级关系。枚举完后，并查集就形成了一颗新树，每个节点的深度即为答案（根节点深度为1）。

　　模拟过程：假设一开始的图是： 3 - 1 - 4 - 2

　　从小到大枚举权值：

　　第一个是1，相邻的点为3,4，都没有遍历过，所以1单独成一个连通块。

　　

 

 　　第二个是2，相邻的点为4，都没有遍历过，所以2单独成一个连通块。

　　

 

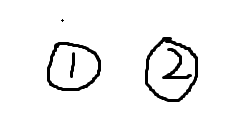
 　　第三个是3，相邻的点为1，说明1所在连通块是因为3而拆出来的，现在合回去。

　　

 

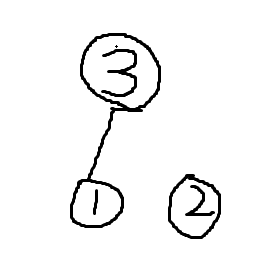
 　　第四个是4，相邻的点为1,2，说明1,2的连通块是因为4拆出来的，连通0块1的根是3，连通块2的根是2，合起来。

　　

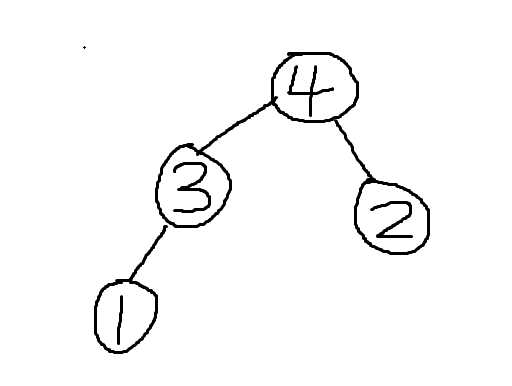
 　　这颗就是新的树了，根据并查集的关系建出来的树。

　　如果看着这颗树，按一开始的思路进行拆连通块统计贡献，就会发现，每在一个连通块上删一个最大值，就相当于在这颗树上删去那个点，然后这个点包含的子树贡献全部+1，和一开始的想法一样，删着删着就会发现节点深度就是我们维护的贡献，妙啊。

 

　　反思：这道题删一个点形成多个连通块，而并查集维护的是连通块，所以应该往并查集这个方向想？有没有大佬指点下思路应该怎么往这个方向靠近啊....

 

代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 7;
vector<int> E[maxn],tu[maxn];
int n,fa[maxn],dep[maxn];
struct node {
    int x,val;
}a[maxn];
bool cmp(node a,node b) {
    return a.val < b.val;
}
int fid(int x) {
    return x == fa[x] ? x : fa[x] = fid(fa[x]);
}
void dfs(int u,int fa) {
    dep[u] = dep[fa] + 1;
    for (auto v:tu[u]) {
        if(v == fa) continue;
        dfs(v,u);
    }
}
void solve() {
    int x,y;
    scanf("%d",&n);
    for (int i=1; i<=n; ++i) {
        E[i].clear();
        tu[i].clear();
        fa[i] = dep[i] = 0;
    }
    for (int i=1; i<=n-1; ++i) {
        scanf("%d%d",&x,&y);
        E[x].push_back(y);
        E[y].push_back(x);
    }
    for (int i=1; i<=n; ++i) {
        scanf("%d",&a[i].val);
        a[i].x = i;
    }
    sort(a+1,a+1+n,cmp);
    for (int i=1; i<=n; ++i) {
        fa[a[i].x] = a[i].x;
        for (auto v:E[a[i].x]) {
            if(fa[v]) {
                int V = fid(v);
                fa[V] = a[i].x; 
                tu[V].push_back(a[i].x);
                tu[a[i].x].push_back(V);
            }
        }
    }
    dfs(a[n].x,0);
    for (int i=1; i<=n; ++i) printf("%d\n",dep[i]);
}
int main() {
    int t;
    scanf("%d",&t);
    while(t--) {
        solve();
    }
    return 0;
}