HDU - 2196(树形DP)
题目:
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.
InputInput file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.OutputFor each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).Sample Input
5 1 1 2 1 3 1 1 1
Sample Output
2 3 4 4
题意:
不知道多少组测试样例,第一行一个n,代表有多少台电脑,接下来有n-1行,每行两个数a,b,第i行(2<=i<=n)表示编号为i的电脑连接编号为a的电脑,他们的距离是b(即电缆长度),问每台电脑到其最远点距离
思路:树形DP(感谢大佬的视频讲解 https://www.bilibili.com/video/av12194537?t=1863)
我们定义f【i】表示编号为i的节点第一步向儿子方向走的最远距离
g【i】表示编号为i的节点第一步向父亲方向走的最远距离
p【i】表示编号为i的节点的父亲节点编号
w(a,b)表示编号a节点到编号b节点的距离,a和b是一条边连接的,即边权
用2个dfs求出这三个数组
递推式:f【u】=max(f【v】,w(u,v))//v是u的孩子
g【u】=w(u,p【u】)+max(g【p【u】】,f【v】+w(p【u】,u))//v是u的兄弟
两个递推式在下面讲解
对于第i个节点,答案就是max(f【i】,g【i】)
因为对一个节点来说,它的第一步只能是向孩子方向走(可能有多个孩子)或者向父亲方向走
第一遍dfs求出f和p数组,我们默认1节点是根节点,它的父亲节点是0(假想)
这个深搜很容易理解,直接上代码

long long int dfs1(int u,int fa) {//u节点走孩子方向的最大距离 for(int i=0;i<E[u].size();++i){ int v=E[u][i].first; int w=E[u][i].second; if(v!=fa) f[u]=max(f[u],dfs1(v,p[v]=u)+w); /*要么是当前值(可能有多个孩子),要么是当前点到孩子点的距离加上f【v】*/ } return f[u]; }
第二遍dfs求出g数组,看图(假设边权都为1)
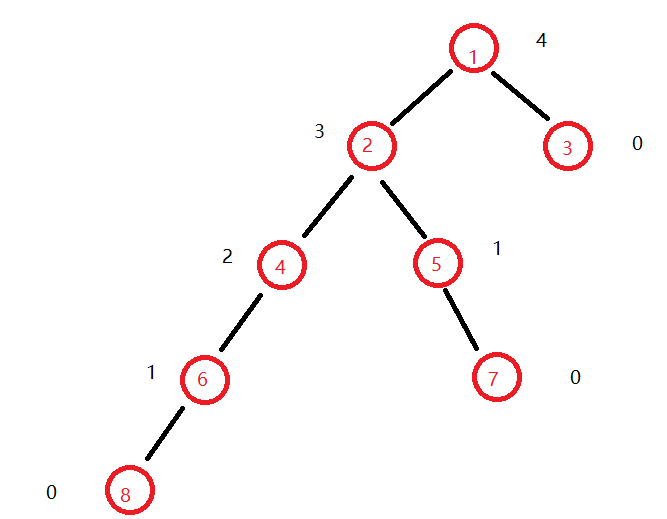
图中红色数字为节点编号,黑色数字表示f【u】的值(第一遍dfs求出),即当前节点第一步向孩子方向走的最大距离
第一遍dfs,相当于从下往上进行动态规划,而第二遍dfs,则是从上往下进行动态规划
怎么用f和p数组算出g数组呢
假设我们要求节点u的g,令fa是u节点的父亲节点
首先,g【u】=g【fa】(假设第一步往上走且第二步也是往上走的距离最大)
然后遍历fa连接的所有节点
若找到fa的父亲节点,跳过,因为我们一开始就假设走这条路
若找到u节点,跳过,跑回来干嘛
若找到其他节点(必然为u节点的兄弟节点,我们设为v,v可能有多个,也可能没有)
则比较g【u】和w(fa,v)+f【v】的大小,即比较第二步往上走好一点还是往下走好一点
遍历完之后,g【u】加上w(fa,u),就成功把g【u】算出来了
我们看出,要想求g【u】,就要先知道g【fa】,即要先知道上面节点的g,才能求下面节点的g
所以,这是一个从上往下走的过程
对于根节点的计算,我们不存在w(0,1)所以还要注意一下边界问题
代码实现:

void dfs2(int u,int fa) { int t=0; g[u]=g[fa]; for(int i=0;i<E[fa].size();++i){ int v=E[fa][i].first; int w=E[fa][i].second; if(v==p[fa]) continue;//fa的父亲节点,跳过 if(v==u) t=w;//又跑回来了,跳过 else g[u]=max(g[u],f[v]+w);//更新 } g[u]+=t; for(int i=0;i<E[u].size();++i){//dfs孩子节点,更新下面的g int v=E[u][i].first; int w=E[u][i].second; if(v!=fa) dfs2(v,u); } }
我们模拟跑一下dfs2,从根节点开始
首先g【1】=g【0】=0;然后编号0节点是虚拟的,没有连接任何点,所以g【1】=0;
求节点2,g【2】=g【1】=0;然后遍历编号1节点连接的所有点
找到节点2,跳过,找到节点3,更新g【2】=max(g【2】,w(1,3)+f【3】)=max(0,1+0)=1;
遍历完后,我们加上w(1,2)=1,所以g【2】=1+1=2;
求节点4,g【4】=g【2】=2;然后遍历编号2节点连接的所有点
找到节点1,1是2的父亲节点,跳过
找到节点4,跳过
找到节点5,更新g【4】=max(g【4】,w(2,5)+f【5】)=max(2,1+1)=2;
遍历完后,我们加上w(2,4)=1,所以g【4】=2+1=3;
......
这样就更新好了g数组
然后答案就是max(f【i】,g【i】)啦,第一步要么向孩子方向走,要么向父亲方向走,找二者最大就行了
完整代码:

#include <bits/stdc++.h> #define mp make_pair using namespace std; typedef long long int ll; const int maxn=1e5+10; vector<pair<int,int> > E[maxn]; long long int f[maxn],g[maxn],p[maxn]; long long int dfs1(int u,int fa) {//u节点走孩子方向的最大距离 for(int i=0;i<E[u].size();++i){ int v=E[u][i].first; int w=E[u][i].second; if(v!=fa) f[u]=max(f[u],dfs1(v,p[v]=u)+w); } return f[u]; } void dfs2(int u,int fa) { int t=0; g[u]=g[fa]; for(int i=0;i<E[fa].size();++i){ int v=E[fa][i].first; int w=E[fa][i].second; if(v==p[fa]) continue; if(v==u) t=w; else g[u]=max(g[u],f[v]+w); } g[u]+=t; for(int i=0;i<E[u].size();++i){ int v=E[u][i].first; int w=E[u][i].second; if(v!=fa) dfs2(v,u); } } int main() { int n; while(cin>>n) { for(int i=1;i<=n;++i) E[i].clear(); memset(f,0,sizeof(f)); memset(g,0,sizeof(g)); memset(p,0,sizeof(p)); for(int i=2;i<=n;++i){ int a,b; scanf("%d%d",&a,&b); E[a].push_back(mp(i,b)); E[i].push_back(mp(a,b)); } dfs1(1,0); dfs2(1,0); for(int i=1;i<=n;++i){ printf("%lld\n",max(f[i],g[i])); } } return 0; }



