第5章学习小结

这章讲了树，详细定义就翻翻书吧，下面讲讲两道题

1.深入虎穴

这题也是天梯赛的题目，当时我一看，感觉一个深搜就完事了，然而全错。。。。。

为什么？为什么？

后来等老师讲了这道题后，我才发现，原来要找根节点，我一直以为题目默认了1是根节点

教训：当你觉得你思路没问题但是答案有错，尝试一下重新读题

题解的话老师都说的很详细了，还带着我们打了一遍，我就简单介绍一下STL中vector的用法吧

vector可以说是一个动态数组，你可以不断往里面塞数据，不需要自己分配它的空间

比如vector<int> E；就定义了一个整形数组E，它的容量可以到100，可以到100000，也可以更多，自己不用考虑为他分配多大空间

首先，把头文件<vector>弄进来

然后是定义

vector<int> E；//不一定是int,可以写char，也可以写自己定义的结构体类型

尾部插入元素：E.push_back(a);//a为要插入的元素，a是int型，下面的相同

下标访问（从0开始）如a=E[0]；

查看目前有多少个元素：E.size();

删除元素

　　E.erase(E.begin()+2);删除第3个元素

　　E.erase(E.begin()+i,E.end()+j);删除区间[i,j-1];区间从0开始

清空数组：E.clear();

当然还有很多操作，要用的时候问下度娘就可以了

AC代码：

#include <iostream>
#include <queue>
#include <string.h>
#include <stdio.h>
#include <vector>
using namespace std;
const int maxn = 1e5+10;
queue<int>q;
vector<int>E[maxn];
bool vis[maxn];
int N,to,ans=0,step_max=0;
void dfs(int rt,int step)
{
    if(step>step_max) {
        ans=rt;
        step_max=step; 
    }
    for(int i=0;i<E[rt].size();++i){
        int to=E[rt][i];
        if(vis[to]) continue;
        vis[to]=1;
        dfs(to,step+1);
    }    
}
int main()
{
    vis[1]=1;
    int step=1,root=1;
    scanf("%d",&N);
    for(int i=1;i<=N;++i){
        int num;
        scanf("%d",&num);
        while(num--)
        {
            scanf("%d",&to);
            E[i].push_back(to);
            vis[to]=1;
        }
    }
    for(int i=1;i<=N;++i)
    if(!vis[i]) {
        root=i;
        break;
    }
    if(N<=0) {
        printf("%d",0);
        return 0;
    }
    memset(vis,0,sizeof(vis));
    dfs(root,1);
    printf("%d",ans);
    return 0;
}

View Code

2.To the moon（主席树裸题）----------学习笔记

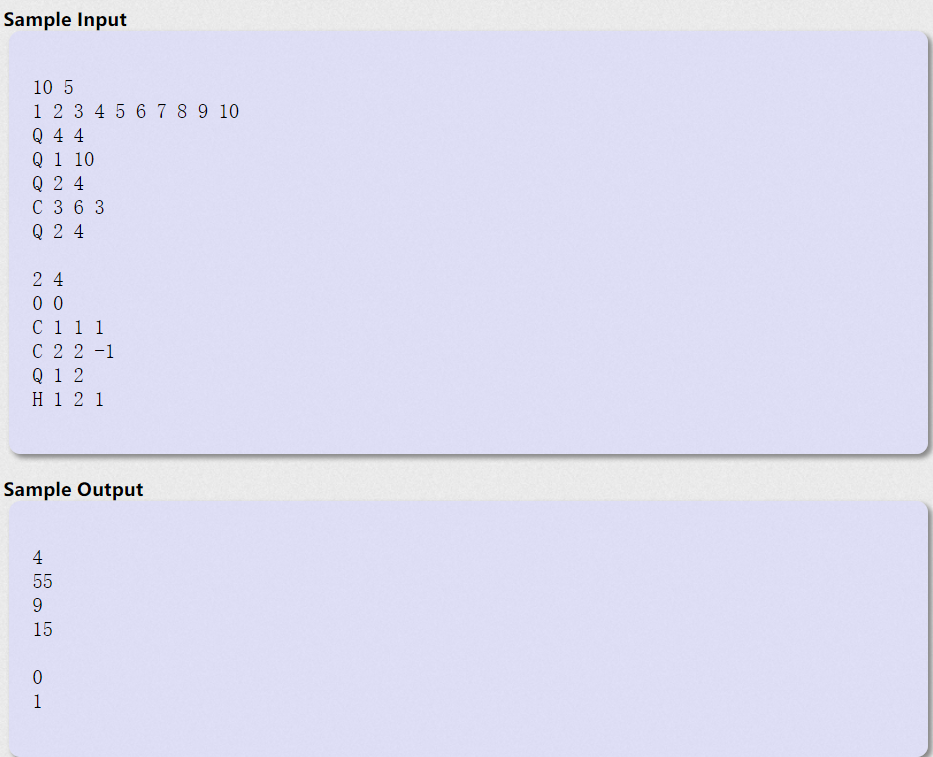
题意：给你一组数字，有以下操作：

1.C l r d C操作表示从第l个元素到第r个元素，每个元素的值都加上d，并且时间戳+1（时间戳一开始为0）

2.Q l r Q操作表示查询当前时间戳第l个元素到第r个元素的和

3.H l r t　 H操作表示查询在时间戳是t的时候，第l个元素到第r个元素的和

4.B t B操作表示回到时间戳为t的时候

拿第二个样例来说

时间戳为0时元素值：0 0

时间戳为1时元素值：1 0

时间戳为2时元素值：1 -1

Q 1 2：1+（-1）=0

H 1 2 1：在时间戳为1的时候，元素值分别是1和0，他们的和是1

我们看出，有查询不同时间段的操作，也就是说我们要保留不同时间段数据的信息

如果有n次改动，我们建n+1棵线段树的话（原数组也建一棵），内存肯定不够

怎么办呢？

聪明的Acmer就想到

不同的树之间有着一样的数据

也就是说，不同的树可以共用一些相同的部分，这样就节约了空间

举个栗子，拿第二个样例来说

先看一下不同时间戳下树的样子

绿色部分代表时间戳为0的树变到时间戳为1的时候不变的部分

红色部分代表时间戳为1的树变到时间戳为2的时候不变的部分

如果我们把相同部分的信息利用起来建树，就变成了

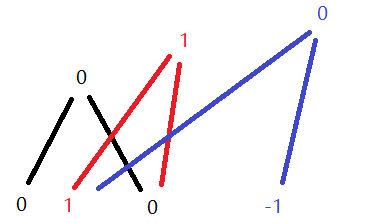
原本需要3*3=9个空间，现在只需要7个空间

如果数据大一点的话，就可以节省很多空间

思想大概就是这样，下面来看实现

先定义要用的东西

const int N=1e5+5,M=2.5e6+5;
typedef long long LL;
int ls[M],rs[M],tail,now,root[N];
LL add[M],sum[M];

解释：ls[i]表示编号为i的节点的左子树

　　　rs[i]表示编号为i的节点的右子树

　　　tail用来给树的节点编号，从1开始

　　　now表示当前时间戳

　　　root[i]表示时间戳为i的线段树的根节点编号

　　　add[i]表示节点i的懒惰标记

　　　sum[i]表示节点i的信息（区间和）

初始化：

void pushup(int id)
{
    sum[id]=sum[ls[id]]+sum[rs[id]];    
}
void init(int id,int L,int R)//id为当前节点编号，L，R表示区间【L，R】
{
    add[id]=0;//懒惰标记置0
    if(L==R){
        scanf("%lld",sum+id);
        return ;
    }
    int mid=L+R>>1;
    init(ls[id]=tail++,L,mid);//初始化左子树
    init(rs[id]=tail++,mid+1,R);//初始化右子树
    pushup(id);//当前节点的和等于左右孩子的和
}

View Code

更新线段树：

int Add(int id,int L,int R,int l,int r,int v)//l，r表示要修改的区间，v为要加的值，注意这里的id是上一棵树对应位置的节点编号，新树的节点编号是cur
{
    if(l>R||L>r) return id;//走错位置，回去回去
     int cur=tail++;//给节点一个编号
    add[cur]=add[id];//继承上一棵树的懒惰标记
    sum[cur]=sum[id]+(min(R,r)-max(L,l)+1)*v;//更新区间和
    if(l<=L && R<=r){//发现不需要弄出新的节点，直接连上旧的节点
        add[cur]+=v;
        ls[cur]=ls[id];
        rs[cur]=rs[id];
    }
    else {//需要弄出新的节点，继续开新节点
        int mid = L+R>>1; 
        ls[cur]=Add(ls[id],L,mid,l,r,v);
        rs[cur]=Add(rs[id],mid+1,R,l,r,v);
    }
    return cur;
}

View Code

查询：

LL query(int id,int L,int R,int l,int r)//id为当前节点，L，R为当前区间，l，r为查询区间
{
    if(l>R||L>r) return 0;
    if(l<=L && R<=r) return sum[id];
    int mid = L + R >> 1;
    return add[id]*(min(R,r)-max(l,L)+1)+query(ls[id],L,mid,l,r)+query(rs[id],mid+1,R,l,r);//注意一下这里的min和max，自己画一下图很容易看出来
}

View Code

完整代码：

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=2.5e6+5;
typedef long long LL;
int ls[M],rs[M],tail,now,root[N];
LL add[M],sum[M];
void pushup(int id)
{
    sum[id]=sum[ls[id]]+sum[rs[id]];    
}
void init(int id,int L,int R)
{
    add[id]=0;
    if(L==R){
        scanf("%lld",sum+id);
        return ;
    }
    int mid=L+R>>1;
    init(ls[id]=tail++,L,mid);
    init(rs[id]=tail++,mid+1,R);
    pushup(id);
}
int Add(int id,int L,int R,int l,int r,int v)
{
    if(l>R||L>r) return id;
     int cur=tail++;
    add[cur]=add[id];
    sum[cur]=sum[id]+(min(R,r)-max(L,l)+1)*v;
    if(l<=L && R<=r){
        add[cur]+=v;
        ls[cur]=ls[id];
        rs[cur]=rs[id];
    }
    else {
        int mid = L+R>>1; 
        ls[cur]=Add(ls[id],L,mid,l,r,v);
        rs[cur]=Add(rs[id],mid+1,R,l,r,v);
    }
    return cur;
}
LL query(int id,int L,int R,int l,int r)
{
    if(l>R||L>r) return 0;
    if(l<=L && R<=r) return sum[id];
    int mid = L + R >> 1;
    return add[id]*(min(R,r)-max(l,L)+1)+query(ls[id],L,mid,l,r)+query(rs[id],mid+1,R,l,r);
}


int main()
{
    int n,m;
    while(cin>>n>>m)
    {
        now=0;tail=0;init(root[now]=tail++,1,n);
        char op[2];
        int l,r,d,t;
        while(m--)
        {
            scanf("%s",&op);
            getchar();
            if(op[0]=='C') {
                scanf("%d%d%d",&l,&r,&d);
                ++now;
                root[now]=Add(root[now-1],1,n,l,r,d);
            }
            else if(op[0]=='Q'){
                scanf("%d%d",&l,&r);
                printf("%lld\n",query(root[now],1,n,l,r));
            }
            else if(op[0]=='H'){
                scanf("%d%d%d",&l,&r,&t);
                printf("%lld\n",query(root[t],1,n,l,r));
            }
            else {
                scanf("%d",&t);
                now=t;
            }
        }
    }
    
    return 0;
}

View Code

从理解代码到能自己敲代码是个很艰难的过程

这个代码我就看了三个小时

一边画图，一边自己出样例，终于理解了

理解过程中我觉得画图理解是最实用的

但是要自己敲的话可能还有点难度

上次指定的目标达到了（熟悉string）

下一次的目标是理解和敲出树链剖分

posted @ 2019-05-03 11:31 丿不落良辰阅读(164) 评论(1) 编辑收藏举报

刷新页面返回顶部

丿不落良辰

第5章学习小结

公告