高数叔 笔记
引子
三角函数相关公式
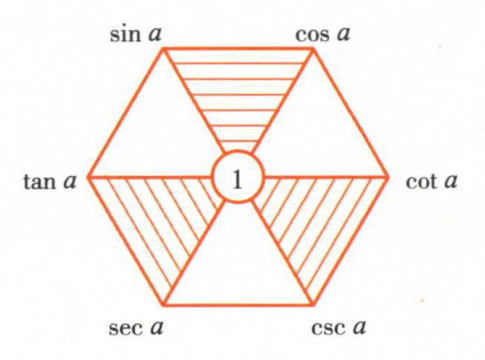
(1)三角函数六边形记忆
对角线连接的两个三角函数乘积为1:
\(
\sin a \cdot \csc a=1,\\
\cos a \cdot \sec a=1,\\
\tan a \cdot \cot a=1
\)
对于阴影部分的三角形上面两个端点的平方等于下面两个端点的平方
\(
\sin^2 a+\cos^2a=1^2,\\
\tan^2 a+1^2=\sec^2 a,\\
1^2+\cot^2 a=\csc^2 a
\)
六边形的每个端点都等于相邻两个端点的乘积:
\(
\sin a=\tan a \cdot \cos a,\\
\cos a=\sin a \cdot \cot a,\\
\cot a=\cos a \cdot \csc a,\\
\csc a=\cot a \cdot \sec a,\\
\sec a=\csc a \cdot \tan a,\\
\tan a=\sec a \cdot \sin a
\)
(2) 两角和与差公式:
\(
\sin(a+b)=\sin a \cos b+ \cos a \sin b,\\
\sin(a-b)=\sin a \cos b=\cos a \sin b,\\
\cos(a+b)=\cos a \cos b-\sin a \sin b,\\
\cos(a-b)=\cos a \cos b+\sin a \sin b
\)
(3) 二倍角公式
\(
\sin 2a= 2\sin a \cos a,\\
\cos 2a=\cos^2 a-\sin^2 a= 2\cos^2 a-1=1-2\sin^2 a,\\
\tan 2a=\frac{2\tan a}{1-\tan^2a}
\)
(4)和差化积公式:
\(
\sin a +\sin b=2sin\frac{a+b}{2} \cdot \cos\frac{a-b}{2},\\
\sin a -\sin b=2cos\frac{a+b}{2} \cdot \sin\frac{a-b}{2},\\
\cos a +\cos b=2cos\frac{a+b}{2} \cdot \cos\frac{a-b}{2},\\
\cos a -\cos b=2sin\frac{a+b}{2} \cdot \sin\frac{a-b}{2},
\)
(5) 积化和差公式:
\(
\sin a \cdot \cos b=\frac {1}{2} [\sin(a+b)+\sin(a-b)],\\
\cos a \cdot \sin b=\frac {1}{2} [\sin(a+b)+\sin(a-b)],\\
\cos a \cdot \cos b=\frac {1}{2} [\cos(a+b)+\cos(a-b)],\\
\sin a \cdot \sin b=\frac {1}{2} [\cos(a+b)+\cos(a-b)],
\)
二项式定理
对于任意的正整数n,
\( (a+b)^n=a^n+C^1_n a^{n-1}b+C^2_n a^{n-2}b^2+...+C^{n-1}_n a^{n-1}b^n \)
整数幂的差
\(a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+...+ab^{n-2}b{n-1}),n>0\)
等差数列
\( 通项:a_n=a_1+(n-1)d 前n项和:Sn=\frac{(a_1+a_n)n}{2}=a_1n+\frac {n(1-1)}{2}d \)
等差数列
\( 通项:a_n=a_1 \cdot q^{n-1} 前n项和:Sn=\frac{a_1(1-q^n)}{1-q} \)
极限
数列的极限
证明:\(\lim\limits_{x\rightarrow\infty}\frac{3n+1}{2n+1}=\frac{3}{2}\)
\(分析:要使|\frac{3n+1}{2N+1}|=\frac{1}{2(2n+1)}小于\varepsilon ,为了计算方便,我们可以将距离放大,比如|\frac{3n+1}{2N+1}|=\frac{1}{2(2n+1)}<\frac{1}{4n}<\varepsilon,\\只要满足\frac{1}{4n}<\varepsilon 就能保证\frac{1}{2(2n+1)}<\varepsilon,也就是只需要满足n>\frac{1}{4\varepsilon} 即可\\
证明: 因为对\forall\varepsilon>0,\exists N=[\frac{1}{4\varepsilon}],当n<N时,有\frac{3n+1}{2N+1}|<\varepsilon,所以\lim\limits_{x\rightarrow\infty}\frac{3n+1}{2n+1}=\frac{3}{2}\)
函数的极限
\(利用定义证明\lim\limits_{x\rightarrow3}(3x-1)=8\)
\(
分析:因为|(3x-1)-8|=3|x-3|,要使|(3x-1)-8|<\varepsilon,只需\\
3|x-3|<\varepsilon,也就是|x-3|<\frac{\varepsilon}{3}.\\
证明:因为\varepsilon>0,\exists\delta,当0<|x-3|<\delta时,有|(3x-1)-8|<\varepsilon,所\\以有
\lim\limits_{x\rightarrow3}(3x-1)=8
\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号