Caffe源码-几种优化算法
SGD简介
caffe中的SGDSolver类中实现了带动量的梯度下降法,其原理如下,\(lr\)为学习率,\(m\)为动量参数。
- 计算新的动量:
history_data = local_rate * param_diff + momentum * history_data
\(\nu_{t+1}=lr*\nabla_{\theta_{t}}+m*\nu_{t}\) - 计算更新时使用的梯度:
param_diff = history_data
\(\Delta\theta_{t+1}=\nu_{t+1}\) - 应用更新:
param_data = param_data - param_diff
\(\theta_{t+1}=\theta_{t}-\Delta\theta_{t+1}\)
步骤1和步骤2均在SGDSolver类的ComputeUpdateValue()函数中实现,步骤3对每个优化方法来说都是相同的,代码可参考之前的博客:Caffe源码-SGDSolver类。
NAG(Nesterov Accelerated Gradient)简介
NAG算法在NesterovSolver类中实现,NAG与SGD相比唯一区别在于梯度的计算上。如上,SGD使用的梯度是参数\(\theta_{t}\)在当前位置的梯度\(\nabla_{\theta_{t}}\),而NAG中使用的是当前参数\(\theta_{t}\)在施加了动量之后的位置的梯度\(\nabla_{(\theta_{t}-m*\nu_{t})}\),其原理为:
- 应用临时更新:\(\tilde{\theta}_{t+1}=\theta_{t}-m*\nu_{t}\)
- 计算该位置的梯度:\(\nabla_{\tilde{\theta}_{t+1}}\)
- 计算新的动量:\(\nu_{t+1}=lr*\nabla_{\tilde{\theta}_{t+1}}+m*\nu_{t}\)
- 得到更新时使用的梯度:\(\Delta\theta_{t+1}=\nu_{t+1}\)
- 应用更新:\(\theta_{t+1}=\theta_{t}-\Delta\theta_{t+1}\)
网络上有一张常见的图用于表示SGD和NAG的过程。
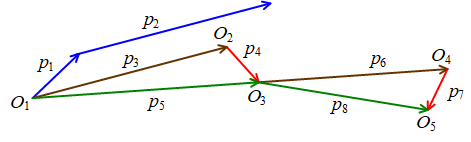
对于SGD算法,蓝色向量\(p_{1}\)为当前参数\(\theta_{t}\)在该位置的梯度\(lr*\nabla_{\theta_{t}}\),蓝色向量\(p_{2}\)为动量\(m*\nu_{t}\),而\(p_{1}+p_{2}\)即为参数一次的更新量\(\Delta\theta_{t+1}\)。
对于NAG算法,\(O_{1}\)为参数\(\theta_{t}\)的初始位置,棕色向量\(p_{3}=p_{2}\),先计算运用动量后的参数\(\tilde{\theta}_{t+1}\)的位置\(O_{2}\),然后计算该位置梯度\(\nabla_{\tilde{\theta}_{t+1}}\),即为图中的红色向量\(p_{4}\),而\(p_{5}=p_{3}+p_{4}\)即为参数一次的更新量\(\Delta\theta_{t+1}=\nu_{t+1}\)。之后仿照该步骤计算下一次迭代的动量\(m*\nu_{t+1}\)(棕色向量\(p_{6}\))和梯度\(\nabla_{\tilde{\theta}_{t+2}}\)(红色向量\(p_{7}\)),得到更新量\(p_{8}\)。
NAG算法的原理还是很好理解的,但是实现起来却有一个非常难理解的地方,即如何计算参数临时更新位置的梯度\(\nabla_{\tilde{\theta}_{t+1}}\)?神经网络这种复杂的系统中想要根据当前位置的梯度\(\nabla_{\theta_{t}}\)来估算另一位置的梯度\(\nabla_{\tilde{\theta}_{t+1}}\)几乎是不可能的。网络上关于该算法的实现细节非常少,不过结合caffe代码和其他的开源代码等,可以判断出,NAG算法每次迭代时保存的参数是临时参数\(\tilde{\theta}_{t+1}\)(位置\(O_{2}\)),而非初始\(O_{1}\)位置处的参数\(\theta_{t}\),这样每次反向传播计算出的梯度实际上就是红色向量\(p_{4}\)。然后每次更新时,会根据动量\(p_{3}\)先将参数从位置\(O_{2}\)退回\(O_{1}\),然后计算得到一次迭代的更新量\(p_{5}\),使参数更新\(\theta_{t+1}\)(位置\(O_{3}\)),并保存下一次迭代时需要使用的临时参数\(\tilde{\theta}_{t+2}\)(位置\(O_{4}\))。
nesterov_solver.cpp源码
//根据当前迭代次数对应的学习率rate,计算网络中第param_id个可学习参数在更新时使用的梯度
template <typename Dtype>
void NesterovSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //网络中的所有可学习参数
const vector<float>& net_params_lr = this->net_->params_lr(); //网络中每个参数对应的学习率系数
Dtype momentum = this->param_.momentum(); //求解器设置的动量
Dtype local_rate = rate * net_params_lr[param_id]; //得到当前参数对应的学习率
switch (Caffe::mode()) {
case Caffe::CPU: { //CPU模式
// save history momentum for stepping back
caffe_copy(net_params[param_id]->count(), this->history_[param_id]->cpu_data(),
this->update_[param_id]->mutable_cpu_data()); //将历史数据history_拷贝至update_中,update_data = history_data
// update history //history_data = local_rate * net_params_diff + momentum * history_data
caffe_cpu_axpby(net_params[param_id]->count(), local_rate, net_params[param_id]->cpu_diff(), momentum,
this->history_[param_id]->mutable_cpu_data());
// compute update: step back then over step //update_data = (1 + momentum) * history_data + (-momentum) * update_data
caffe_cpu_axpby(net_params[param_id]->count(), Dtype(1) + momentum,
this->history_[param_id]->cpu_data(), -momentum,
this->update_[param_id]->mutable_cpu_data());
// copy //net_params_diff = update_data
caffe_copy(net_params[param_id]->count(), this->update_[param_id]->cpu_data(),
net_params[param_id]->mutable_cpu_diff());
break;
}
case Caffe::GPU: {
#ifndef CPU_ONLY
// gpu的操作同理
// h_temp = history_data
// history_data = momentum * h_temp + local_rate * net_params_diff
// net_params_diff = (1+momentum) * history_data - momentum * h_temp
nesterov_update_gpu(net_params[param_id]->count(), net_params[param_id]->mutable_gpu_diff(),
this->history_[param_id]->mutable_gpu_data(), momentum, local_rate);
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
对应上述的说明,代码中的各步操作为:
- 当前迭代的动量\(\nu_{t}\):
update_data = history_data net_params_diff为临时位置的参数的梯度\(\nabla_{\tilde{\theta}_{t+1}}\),计算新的动量:history_data = local_rate * net_params_diff + momentum * history_data
\(\nu_{t+1}=lr*\nabla_{\tilde{\theta}_{t+1}}+m*\nu_{t}\)- 计算下一次迭代的临时参数相对于当前临时参数的更新量\(\Delta\tilde{\theta}_{t+2}\):
update_data = (1 + momentum) * history_data + (-momentum) * update_data
\(\Delta\tilde{\theta}_{t+2}=(1+m)*\nu_{t+1}-m*\nu_{t}\)
注意,当前临时参数在位置\(O_{2}\),需要减去向量\(p_{3}\)(\(p_{3}=m*\nu_{t}\)),再加上向量\(p_{5}\)和\(p_{6}\)(\(p_{5}=\nu_{t+1},p_{6}=m*\nu_{t+1}\))才能得到新的临时位置\(O_{4}\)。 - 保存参数更新量:
net_params_diff = update_data - 应用更新:\(\tilde{\theta}_{t+2}=\tilde{\theta}_{t+1}-\Delta\tilde{\theta}_{t+2}\)
AdaGrad简介
AdaGrad算法通过缩放每个参数反比于其所有梯度历史平方值总和的平方跟,可使得具有较大梯度的参数能够快速下降,使具有小偏导的参数能够缓慢下降。
其原理如下,初始累积变量\(r=0\),\(\delta\)为较小常数,防止除法除数过小而不稳定。
- 累加平方梯度(\(\odot\)为逐元素点乘):\(r_{t+1}=r_{t}+\nabla_{\theta_{t}}\odot\nabla_{\theta_{t}}\)
- 计算梯度的更新量:\(\Delta\theta_{t+1}=\frac{lr}{\delta+\sqrt{r_{t+1}}}\odot\nabla_{\theta_{t}}\)
- 应用更新:\(\theta_{t+1}=\theta_{t}-\Delta\theta_{t+1}\)
adagrad_solver.cpp源码
template <typename Dtype>
void AdaGradSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params();
const vector<float>& net_params_lr = this->net_->params_lr();
Dtype delta = this->param_.delta();
Dtype local_rate = rate * net_params_lr[param_id];
switch (Caffe::mode()) {
case Caffe::CPU: {
// compute square of gradient in update
caffe_powx(net_params[param_id]->count(),
net_params[param_id]->cpu_diff(), Dtype(2),
this->update_[param_id]->mutable_cpu_data()); //update_data = net_params ^ 2
// update history
caffe_add(net_params[param_id]->count(),
this->update_[param_id]->cpu_data(),
this->history_[param_id]->cpu_data(),
this->history_[param_id]->mutable_cpu_data()); //history_data = update_data + history_data
// prepare update
caffe_powx(net_params[param_id]->count(), this->history_[param_id]->cpu_data(), Dtype(0.5),
this->update_[param_id]->mutable_cpu_data()); //update_data = history_data ^ 0.5
caffe_add_scalar(net_params[param_id]->count(),
delta, this->update_[param_id]->mutable_cpu_data()); //update_data += delta
caffe_div(net_params[param_id]->count(),
net_params[param_id]->cpu_diff(),
this->update_[param_id]->cpu_data(),
this->update_[param_id]->mutable_cpu_data()); //update_data = net_params_diff / update_data
// scale and copy
caffe_cpu_axpby(net_params[param_id]->count(), local_rate,
this->update_[param_id]->cpu_data(), Dtype(0),
net_params[param_id]->mutable_cpu_diff()); //net_params_diff = local_rate * update_data + 0 * net_params_diff
break;
}
case Caffe::GPU: { //gpu操作同理
#ifndef CPU_ONLY
// gi = net_params_diff;
// hi = history_data = history_data + gi*gi;
// net_params_diff = local_rate * gi / (sqrt(hi) + delta);
adagrad_update_gpu(net_params[param_id]->count(),
net_params[param_id]->mutable_gpu_diff(),
this->history_[param_id]->mutable_gpu_data(), delta, local_rate);
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
AdaGrad/RMSProp/AdaDelta/Adam算法的caffe代码很容易找到对应的公式,不再详细介绍。
RMSProp简介
RMSProp算法在AdaGrad基础上增加一个衰减系数\(\rho\),以便将很早之前的历史梯度数据丢弃。
其原理如下,初始累积变量\(r=0\),\(\delta\)同样为较小常数。
- 累加平方梯度:\(r_{t+1}=\rho*r_{t}+(1-\rho)*\nabla_{\theta_{t}}\odot\nabla_{\theta_{t}}\)
- 计算梯度的更新量:\(\Delta\theta_{t+1}=\frac{lr}{\delta+\sqrt{r_{t+1}}}\odot\nabla_{\theta_{t}}\)
- 应用更新:\(\theta_{t+1}=\theta_{t}-\Delta\theta_{t+1}\)
rmsprop_solver.cpp源码
template <typename Dtype>
void RMSPropSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //所有可学习参数
const vector<float>& net_params_lr = this->net_->params_lr(); //参数对应的学习率系数
// get the learning rate
Dtype delta = this->param_.delta(); //常数delta
Dtype rms_decay = this->param_.rms_decay(); //衰减速率
Dtype local_rate = rate * net_params_lr[param_id]; //参数对应的学习率
switch (Caffe::mode()) {
case Caffe::CPU:
// compute square of gradient in update
caffe_powx(net_params[param_id]->count(), net_params[param_id]->cpu_diff(), Dtype(2),
this->update_[param_id]->mutable_cpu_data()); //update_data = net_params_diff ^ 2
// update history //history_data = (1-rms_decay) * update_data + rms_decay * history_data
caffe_cpu_axpby(net_params[param_id] -> count(), Dtype(1-rms_decay), this->update_[param_id]->cpu_data(),
rms_decay, this->history_[param_id]-> mutable_cpu_data());
// prepare update
caffe_powx(net_params[param_id]->count(), this->history_[param_id]->cpu_data(), Dtype(0.5),
this->update_[param_id]->mutable_cpu_data()); //update_data = history_data ^ 0.5
caffe_add_scalar(net_params[param_id]->count(),
delta, this->update_[param_id]->mutable_cpu_data()); //update_data += delta
//update_data = net_params_diff / update_data
caffe_div(net_params[param_id]->count(), net_params[param_id]->cpu_diff(),
this->update_[param_id]->cpu_data(), this->update_[param_id]->mutable_cpu_data());
// scale and copy
caffe_cpu_axpby(net_params[param_id]->count(), local_rate,
this->update_[param_id]->cpu_data(), Dtype(0),
net_params[param_id]->mutable_cpu_diff()); //net_params_diff = local_rate * update_data + 0 * net_params_diff
break;
case Caffe::GPU:
#ifndef CPU_ONLY
// g = net_params_diff
// h = history_data
// gi = g[i];
// hi = h[i] = rms_decay*h[i] + (1-rms_decay)*gi*gi;
// g[i] = local_rate * g[i] / (sqrt(hi) + delta);
rmsprop_update_gpu(net_params[param_id]->count(),
net_params[param_id]->mutable_gpu_diff(),
this->history_[param_id]->mutable_gpu_data(),
rms_decay, delta, local_rate);
#else
NO_GPU;
#endif
break;
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
AdaDelta简介
AdaDelta也像RMSProp算法一样在AdaGrad基础上增加一个衰减系数\(\rho\),并且还额外维护一个状态量\(x\)。
其原理如下,初始累积变量\(x=0, r=0\),\(\delta\)同样为较小常数。
- 累加平方梯度:\(r_{t+1}=\rho*r_{t}+(1-\rho)*\nabla_{\theta_{t}}\odot\nabla_{\theta_{t}}\)
- 计算不带学习率的梯度的更新量:\(\Delta\tilde{\theta}_{t+1}=\sqrt{\frac{x_{t}+\delta}{r_{t+1}+\delta}}\odot\nabla_{\theta_{t}}\)
- 更新状态量:\(x_{t+1}=\rho*x_{t}+(1-\rho)*\Delta\tilde{\theta}_{t+1}\odot\Delta\tilde{\theta}_{t+1}\)
- 计算带学习率的梯度的更新量:\(\Delta\theta_{t+1}=lr*\Delta\tilde{\theta}_{t+1}\)
与参考 4中的说明不同,caffe代码中仍然有使用学习率\(lr\)。 - 应用更新:\(\theta_{t+1}=\theta_{t}-\Delta\theta_{t+1}\)
adadelta_solver.cpp源码
template <typename Dtype>
void AdaDeltaSolver<Dtype>::AdaDeltaPreSolve() { //AdaDeltaSolver类在构造时会调用该函数
// Add the extra history entries for AdaDelta after those from SGDSolver::PreSolve
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //当前网络中的所有可学习参数
for (int i = 0; i < net_params.size(); ++i) {
const vector<int>& shape = net_params[i]->shape(); //第i个可学习参数的形状
//在SGDSolver<Dtype>::PreSolve中history_已经存入一个与参数blob相同形状的空blob,此处再存入一个
this->history_.push_back(shared_ptr<Blob<Dtype> >(new Blob<Dtype>(shape)));
}
}
#ifndef CPU_ONLY
template <typename Dtype>
void adadelta_update_gpu(int N, Dtype* g, Dtype* h, Dtype* h2, Dtype momentum,
Dtype delta, Dtype local_rate);
#endif
template <typename Dtype>
void AdaDeltaSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //网络中的所有可学习参数
const vector<float>& net_params_lr = this->net_->params_lr(); //每个参数对应的学习率系数
Dtype delta = this->param_.delta(); //AdaDelta方法中的一个参数
Dtype momentum = this->param_.momentum(); //动量系数
Dtype local_rate = rate * net_params_lr[param_id]; //得到当前参数对应的学习率
size_t update_history_offset = net_params.size(); //网络的参数个数
//history_在AdaDeltaPreSolve()中又存入了一次与所有参数形状相同的空blob,下面将
//history_[param_id]表示成 history_former, history_[update_history_offset + param_id]表示成 history_latter
switch (Caffe::mode()) {
case Caffe::CPU: {
// compute square of gradient in update
caffe_powx(net_params[param_id]->count(), net_params[param_id]->cpu_diff(), Dtype(2),
this->update_[param_id]->mutable_cpu_data()); //update_data = net_params_diff ^ 2
// update history of gradients //history_former_data = (1 - momentum) * update_data + momentum * history_former_data
caffe_cpu_axpby(net_params[param_id]->count(), Dtype(1) - momentum, this->update_[param_id]->cpu_data(),
momentum, this->history_[param_id]->mutable_cpu_data());
// add delta to history to guard against dividing by zero later
caffe_set(net_params[param_id]->count(), delta,
this->temp_[param_id]->mutable_cpu_data()); //temp_中每个元素都置为delta, temp_data = delta
caffe_add(net_params[param_id]->count(),
this->temp_[param_id]->cpu_data(),
this->history_[update_history_offset + param_id]->cpu_data(),
this->update_[param_id]->mutable_cpu_data()); //update_data = temp_data + history_latter_data
caffe_add(net_params[param_id]->count(),
this->temp_[param_id]->cpu_data(),
this->history_[param_id]->cpu_data(),
this->temp_[param_id]->mutable_cpu_data()); //temp_data = temp_data + history_former_data
// divide history of updates by history of gradients
caffe_div(net_params[param_id]->count(),
this->update_[param_id]->cpu_data(),
this->temp_[param_id]->cpu_data(),
this->update_[param_id]->mutable_cpu_data()); //update_data = update_data / temp_data
// jointly compute the RMS of both for update and gradient history
caffe_powx(net_params[param_id]->count(),
this->update_[param_id]->cpu_data(), Dtype(0.5),
this->update_[param_id]->mutable_cpu_data()); //update_data = update_data ^ 0.5
// compute the update
caffe_mul(net_params[param_id]->count(),
net_params[param_id]->cpu_diff(),
this->update_[param_id]->cpu_data(),
net_params[param_id]->mutable_cpu_diff()); //net_params_diff = net_params_diff * update_data
// compute square of update
caffe_powx(net_params[param_id]->count(),
net_params[param_id]->cpu_diff(), Dtype(2),
this->update_[param_id]->mutable_cpu_data()); //update_data = net_params_diff ^ 2
// update history of updates //history_latter_data = (1 - momentum) * update_data + momentum * history_latter_data
caffe_cpu_axpby(net_params[param_id]->count(), Dtype(1) - momentum,
this->update_[param_id]->cpu_data(), momentum,
this->history_[update_history_offset + param_id]->mutable_cpu_data());
// apply learning rate
caffe_cpu_scale(net_params[param_id]->count(), local_rate,
net_params[param_id]->cpu_diff(),
net_params[param_id]->mutable_cpu_diff()); //net_params_diff = local_rate * net_params_diff
break;
}
case Caffe::GPU: {
#ifndef CPU_ONLY
// g = net_params_diff;
// h = history_former_data;
// h2 = history_latter_data;
// gi = g[i];
// hi = h[i] = momentum * h[i] + (1-momentum) * gi * gi;
// gi = gi * sqrt((h2[i] + delta) / (hi + delta));
// h2[i] = momentum * h2[i] + (1-momentum) * gi * gi;
// g[i] = local_rate * gi;
adadelta_update_gpu(net_params[param_id]->count(),
net_params[param_id]->mutable_gpu_diff(),
this->history_[param_id]->mutable_gpu_data(),
this->history_[update_history_offset + param_id]->mutable_gpu_data(),
momentum, delta, local_rate);
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
Adam简介
Adam算法包含两个衰减参数\(\rho_{1}\)和\(\rho_{2}\),一般\(\rho_{1}=0.9, \rho_{2}=0.999\)。还包含一阶矩和二阶矩变量\(s, r\),时间步\(t\)。
初始时\(s=0, r=0, t=0\),\(\delta\)同样为较小常数。
-
更新一阶矩:\(s_{t+1}=\rho_{1}*s_{t}+(1-\rho_{1})*\nabla_{\theta_{t}}\)
-
更新二阶矩:\(r_{t+1}=\rho_{2}*r_{t}+(1-\rho_{2})*\nabla_{\theta_{t}}\odot\nabla_{\theta_{t}}\)
-
修正一阶矩的偏差:\(\tilde{s}_{t+1}=\frac{s_{t+1}}{1-\rho_{1}^{t+1}}\)
-
修正二阶矩的偏差:\(\tilde{r}_{t+1}=\frac{r_{t+1}}{1-\rho_{2}^{t+1}}\)
-
计算梯度的更新量:\(\Delta\theta_{t+1}=lr*\frac{\tilde{s}_{t+1}}{\sqrt{\tilde{r}_{t+1}}+\delta}\)
-
应用更新:\(\theta_{t+1}=\theta_{t}-\Delta\theta_{t+1}\)
adam_solver.cpp源码
template <typename Dtype>
void AdamSolver<Dtype>::AdamPreSolve() {
// Add the extra history entries for Adam after those from SGDSolver::PreSolve
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //所有可学习参数
for (int i = 0; i < net_params.size(); ++i) {
const vector<int>& shape = net_params[i]->shape(); //第i个可学习参数对应的形状
this->history_.push_back(shared_ptr<Blob<Dtype> >(new Blob<Dtype>(shape))); //history_再存入一个与参数大小相同的空blob
}
}
#ifndef CPU_ONLY
template <typename Dtype>
void adam_update_gpu(int N, Dtype* g, Dtype* m, Dtype* v, Dtype beta1,
Dtype beta2, Dtype eps_hat, Dtype corrected_local_rate);
#endif
template <typename Dtype>
void AdamSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //所有可学习参数
const vector<float>& net_params_lr = this->net_->params_lr(); //参数的学习率系数
Dtype local_rate = rate * net_params_lr[param_id]; //当前参数的学习率
const Dtype beta1 = this->param_.momentum(); //两个动量系数
const Dtype beta2 = this->param_.momentum2();
// we create aliases for convenience
size_t update_history_offset = net_params.size(); //history_的大小为2 * update_history_offset
Blob<Dtype>* val_m = this->history_[param_id].get();
Blob<Dtype>* val_v = this->history_[param_id + update_history_offset].get();
Blob<Dtype>* val_t = this->temp_[param_id].get();
const int t = this->iter_ + 1; //步数
const Dtype correction = std::sqrt(Dtype(1) - pow(beta2, t)) /
(Dtype(1.) - pow(beta1, t)); //correction = sqrt(1 - beta2 ^ t) / (1 - beta1 ^ t)
const int N = net_params[param_id]->count(); //参数的元素个数
const Dtype eps_hat = this->param_.delta(); //微小值
switch (Caffe::mode()) {
case Caffe::CPU: {
// update m <- \beta_1 m_{t-1} + (1-\beta_1)g_t
caffe_cpu_axpby(N, Dtype(1)-beta1, net_params[param_id]->cpu_diff(), beta1,
val_m->mutable_cpu_data()); //val_m = (1 - beta1) * net_params_diff + beta1 * val_m
// update v <- \beta_2 m_{t-1} + (1-\beta_2)g_t^2
caffe_mul(N, net_params[param_id]->cpu_diff(), net_params[param_id]->cpu_diff(),
val_t->mutable_cpu_data()); //val_t = net_params_diff * net_params_diff
caffe_cpu_axpby(N, Dtype(1)-beta2, val_t->cpu_data(), beta2,
val_v->mutable_cpu_data()); //val_v = (1 - beta2) * val_t + beta2 * val_v
// set update
caffe_powx(N, val_v->cpu_data(), Dtype(0.5),
val_t->mutable_cpu_data()); //val_t = val_v ^ 0.5
caffe_add_scalar(N, eps_hat, val_t->mutable_cpu_data()); //val_t += eps_hat
caffe_div(N, val_m->cpu_data(), val_t->cpu_data(),
val_t->mutable_cpu_data()); //val_t = val_m / val_t
caffe_cpu_scale(N, local_rate*correction, val_t->cpu_data(),
net_params[param_id]->mutable_cpu_diff()); //net_params_diff = local_rate*correction * val_t
break;
}
case Caffe::GPU: {
#ifndef CPU_ONLY
// g = net_params_diff
// m = val_m
// v = val_v
// gi = g[i];
// mi = m[i] = m[i]*beta1 + gi*(1-beta1);
// vi = v[i] = v[i]*beta2 + gi*gi*(1-beta2);
// g[i] = local_rate * correction * mi / (sqrt(vi) + eps_hat);
adam_update_gpu(N, net_params[param_id]->mutable_gpu_diff(),
val_m->mutable_gpu_data(), val_v->mutable_gpu_data(), beta1, beta2,
eps_hat, local_rate*correction);
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
小结
- 很多地方的动量的符号与本文不用,是用\(\nu_{t+1}=-lr*\nabla_{\theta_{t}}+m*\nu_{t}\),然后\(\theta_{t+1}=\theta_{t}+\nu_{t+1}\),其实原理是一致的,本文只是为了保持与caffe的代码一致。
参考
- https://stats.stackexchange.com/questions/179915/whats-the-difference-between-momentum-based-gradient-descent-and-nesterovs-acc
- https://jlmelville.github.io/mize/nesterov.html
- https://zhuanlan.zhihu.com/p/22810533
- https://zh.d2l.ai/chapter_optimization/adadelta.html
- 《Deep Learning》-- Ian Goodfellow and Yoshua Bengio and Aaron Courville
Caffe的源码笔者是第一次阅读,一边阅读一边记录,对代码的理解和分析可能会存在错误或遗漏,希望各位读者批评指正,谢谢支持!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号