最优化作业电子版
- 给定函数\(f(x)=(6+x_1+x_2)^2+(2-3x_1-3x_2-x_1x_2)^2\),求在点\(\hat{X}=(-4,6)^T\)处的最速下降方向和牛顿方向
\[f(x)=(6+x_1+x_2)^2+(2-3x_1-3x_2-x_1x_2)^2\\
\frac{\partial f}{\partial x_1}=(12+2x_1+2x_2)+(4-6x_1-6x_2-2x_1x_2)(-3-x_2)\\
\frac{\partial f}{\partial x_2}=(12+2x_1+2x_2)+(4-6x_1-6x_2-2x_1x_2)(-3-x_1)\\
\hat{X}=(-4,6)^T \\
\nabla f(\hat{X})=(-344,56)^T
\]
最速下降方向为为负梯度方向:\(dk=-g_k=-\nabla f(\hat{X})=(-344,56)^T\)
\[\frac{\partial^2 f}{\partial x_1^2}=2+(-3-x_2)(-6-2x_2)\\
\frac{\partial^2 f}{\partial x_1\partial x_2}=2+(-6-2x_1)(-3-x_2)-(4-6x_1-6x_2-2x_1x_2)\\
\frac{\partial^2 f}{\partial x_2\partial x_1}=2+(-6-2x_2)(-3-x_1)-(4-6x_1-6x_2-2x_1x_2)\\
\frac{\partial^2 f}{\partial x_2^2}=2+(-3-x_1)(-6-2x_1)\\
\]
\[\nabla^2f(X)=\left(\begin{matrix}
2+(-3-x_2)(-6-2x_2)&2+(-6-2x_1)(-3-x_2)-(4-6x_1-6x_2-2x_1x_2)\\
2+(-6-2x_2)(-3-x_1)-(4-6x_1-6x_2-2x_1x_2)&2+(-3-x_1)(-6-2x_1)
\end{matrix}\right)\\
\]
\[\nabla^2f(\hat{X})=\left(\begin{matrix}
164&-56\\
-56&4
\end{matrix}\right)\\
G_k=\nabla^2 f(\hat{X})\\
g_k=\nabla f(\hat{X})\\
G_kd_k=-g_k\\
d_k=G_k^{-1}g_k\\
d_k=\left(\begin{matrix}
-0.7097\\
4.0654
\end{matrix}\right)
\]
牛顿方向为\(d_k=(-0.7097,4.0654)^T\)
-
分别用最速下降法程序和阻尼牛顿法求函数\(f(x_1,x_2)=(x_1-2)^4+(x_1-2x_2)^2\)的极小值点,取初始点为\(x_0=(0,3)^T\)
最速下降法
import numpy as np import tensorflow as tf def fun(x): # return 100 * (x[0] ** 2 - x[1]) ** 2 + (x[0] - 1) ** 2 测试用 return (x[0] - 2) ** 4 + (x[0] - 2 * x[1]) ** 2 def gfun(x): x = tf.Variable(x, dtype=tf.float32) with tf.GradientTape() as tape: tape.watch(x) z = fun(x) return tape.gradient(z, x).numpy() # return np.array([4 * (x[0] - 2) ** 3 + 2 * (x[0] - 2*x[1]), -4 * (x[0] - 2*x[1])]) def grad_wolfe(fun, gfun, x0): maxk = 5000 k = 0 epsilon = 1e-5 while k < maxk: gk = gfun(x0) dk = -gk if np.linalg.norm(dk) < epsilon: break rho = 0.4 sigma = 0.5 a = 0 b = np.inf alpha = 1 while True: if not ((fun(x0) - fun(x0 + alpha * dk)) >= (-rho * alpha * gfun(x0).T @ dk)): b = alpha alpha = (a + alpha) / 2 continue if not (gfun(x0 + alpha * dk).T @ dk >= sigma * gfun(x0).T @ dk): a = alpha alpha = np.min([2 * alpha, (alpha + b) / 2]) continue break x0 = x0 + alpha * dk k += 1 x = x0 val = fun(x) return x, val, k def grad_armijo(fun, gfun, x0): maxk = 5000 rho = 0.5 sigma = 0.4 k = 0 epsilon = 1e-5 while k < maxk: g = gfun(x0) d = -g if np.linalg.norm(d) < epsilon: break m = 0 mk = 0 while m < 20: if fun(x0 + rho ** m * d) < fun(x0) + sigma * rho ** m * g.T @ d: mk = m break m += 1 x0 = x0 + rho ** mk * d k += 1 x = x0 val = fun(x0) return x, val, k if __name__ == '__main__': x0 = np.array([[0.], [3.]]) x, val, k = grad_armijo(fun, gfun, x0) # Armijo准则 print('近似最优点:{}\n最优值:{}\n迭代次数:{}'.format(x, val.item(), k)) x, val, k = grad_wolfe(fun, gfun, x0) # Wolfe准测 print('近似最优点:{}\n最优值:{}\n迭代次数:{}'.format(x, val.item(), k))运行结果:
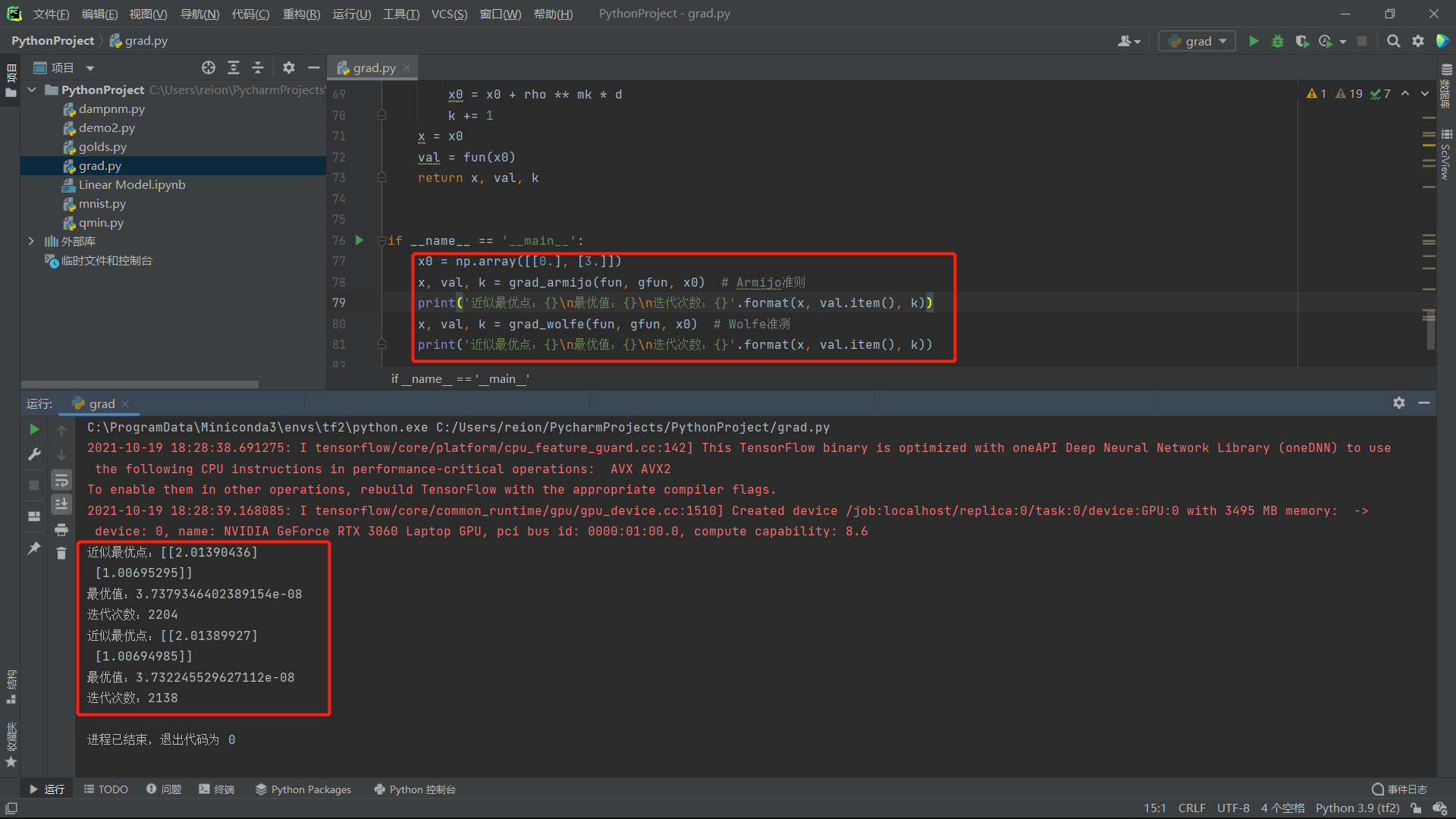
阻尼牛顿法:
import numpy as np
import tensorflow as tf
# def compute_hessian(fun, x):
# mat = []
#
# x1, x2 = tf.Variable(x[0]), tf.Variable(x[1])
# with tf.GradientTape(persistent=True) as tape:
# tape.watch(x1)
# tape.watch(x2)
# z = fun(x)
# for i in x1:
# temp = []
# for j in x2:
# temp.append(tape.gfun(tape.gfun(z, j)[0], i)[0])
# temp = tf.pack(temp)
# mat.append(temp)
# mat = tf.pack(mat)
# return mat
def fun(x):
# return 100 * (x[0] ** 2 - x[1]) ** 2 + (x[0] - 1) ** 2 测试用
return (x[0] - 2) ** 4 + (x[0] - 2 * x[1]) ** 2
def hessian(x):
return np.array([[12 * (x[0] - 2) ** 2 + 2, -4],
[-4, 8]], dtype=np.float32)
def gfun(x):
x = tf.Variable(x)
with tf.GradientTape() as tape:
# tape.watch(x)
z = fun(x)
return tape.gradient(z, x).numpy()
# return np.array([4 * (x[0] - 2) ** 3 + 2 * (x[0] - 2*x[1]), -4 * (x[0] - 2*x[1])])
def dampnm_armijo(fun, gfun, hessian, x0):
maxk = 100
rho = .55
sigma = .4
k = 0
epsilon = 1e-5
while k < maxk:
gk = gfun(x0)
Gk = hessian(x0)
dk = -np.linalg.inv(Gk) @ gk
if np.linalg.norm(gk) < epsilon:
break
m = 0
mk = 0
while m < 20:
if fun(x0 + rho ** m * dk) < fun(x0) + sigma * rho ** m * gk.T @ dk:
mk = m
break
m += 1
x0 = x0 + rho ** mk * dk
k += 1
x = x0
val = fun(x)
return x, val, k
def dampnm_wolfe(fun, gfun, hessian, x0):
maxk = 1000
k = 0
epsilon = 1e-5
while k < maxk:
gk = gfun(x0)
Gk = hessian(x0)
dk = -np.linalg.inv(Gk) @ gk
if np.linalg.norm(gk) < epsilon:
break
# m = 0
rho = 0.4
sigma = 0.5
a = 0
b = np.inf
alpha = 1
# j = 0
while True:
if not ((fun(x0) - fun(x0 + alpha * dk)) >= (-rho * alpha * gfun(x0).T @ dk)):
# j+=1
b = alpha
alpha = (a + alpha) / 2
continue
if not (gfun(x0 + alpha * dk).T @ dk >= sigma * gfun(x0).T @ dk):
a = alpha
alpha = np.min([2 * alpha, (alpha + b) / 2])
continue
break
x0 = x0 + alpha * dk
k += 1
x = x0
val = fun(x)
return x, val, k
if __name__ == '__main__':
x0 = np.array([[0.], [3.]])
# print(fun(x0))
# print(gfun(x0))
# print(hessian(x0))
x, val, k = dampnm_armijo(fun, gfun, hessian, x0) # Armijo准则
print('近似最优点:{}\n最优值:{}\n迭代次数:{}'.format(x, val.item(), k))
x, val, k = dampnm_wolfe(fun, gfun, hessian, x0) # wolfe准则
print('近似最优点:{}\n最优值:{}\n迭代次数:{}'.format(x, val.item(), k))
运行结果:
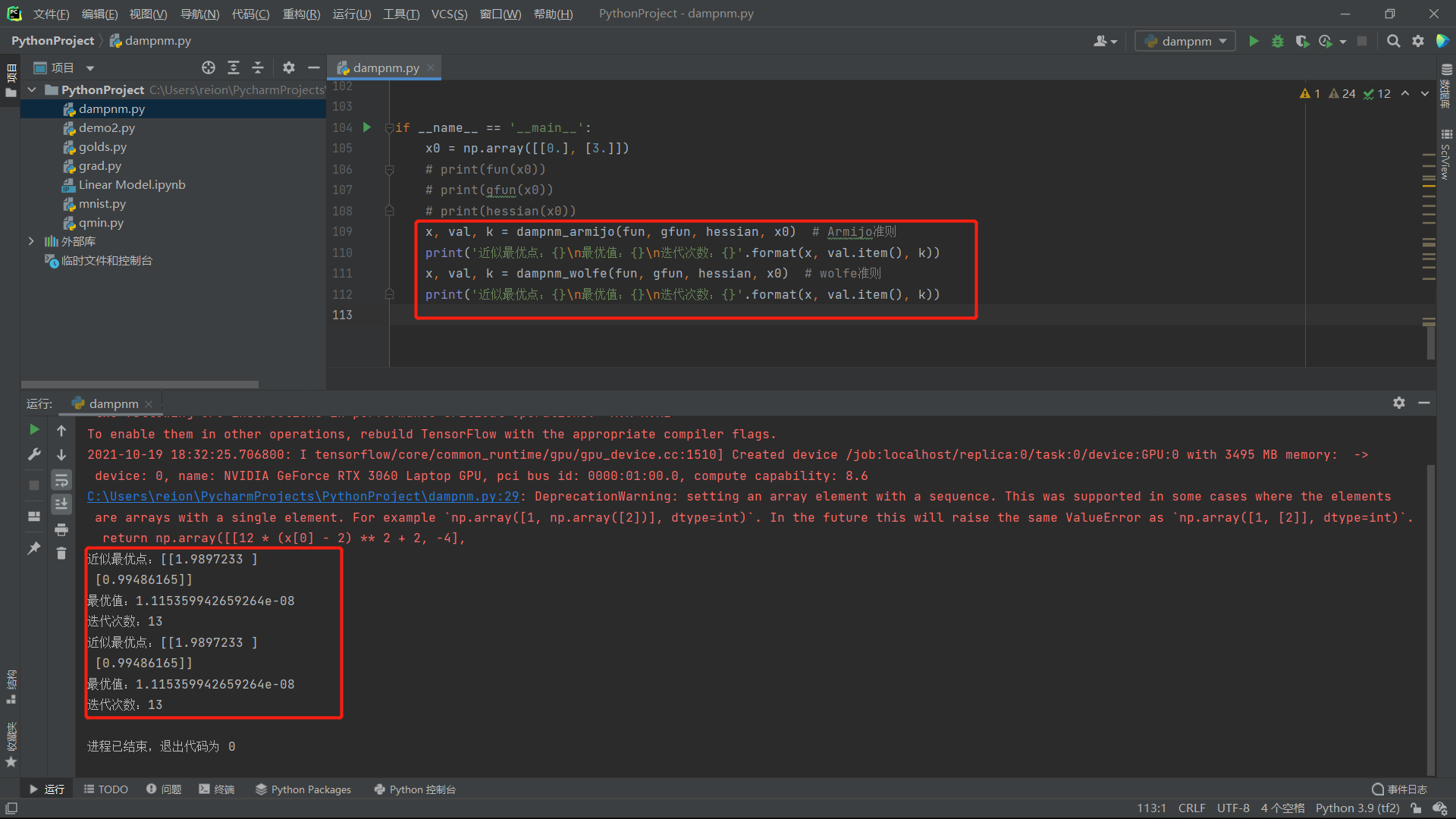



 浙公网安备 33010602011771号
浙公网安备 33010602011771号