树和二叉树
1.树形结构广泛存在我们的现实生活里,如下两张图,第一张是 Linux 文件系统结构,第二张是美国福特汽车公司的汽车家谱图。类似的树形结构还有很多,他们都可以抽象成数据结构里的树。和自然界里的树有所类似又有所不同,他们都有且仅有一个树根,树上的元素都是从树根衍生出来的。不同的是自然界里的树,它的树根在下面,而数据结构里的树,树根在上面。


树是由若干个有限结点组成的一个具有层次关系的集合,每棵树有且仅有一个根,比如在图中,最上面的结点就是树的根结点。例子里的“/”、“etc”、“usr”、“lib”等等都是这棵树上的结点,其中“/”是树的根结点。我们规定根结点是树的第一层,树根的孩子结点是树的第二层,以此类推,树的深度就是结点的最大层数,例如例子里的树,它的深度为 4。
2.树的性质:
- 每棵树有且仅有一个根结点;
- 在树上,从一个结点出发可以访问到其余的结点,并且一个结点到另一个结点的路径有且仅有一条;
- 父亲结点可以有多个孩子结点,除根结点外,其余的结点有且仅有一个父亲结点;
- 根结点没有父亲结点,叶子结点没有孩子结点。
3.二叉树是一种特殊的树,二叉树的每个结点最多只有两个孩子结点,也就是说每个结点最多有两个子树。二叉树有 5 种基本形态:空二叉树,树为空,没有结点;只有根结点的二叉树;只有左子树的二叉树;只有右子树的二叉树;左右子树都有的二叉树。
4.二叉树的性质:
- 二叉树的第 i 层最多有 2i-1 个结点。由定义可知,二叉树的每个结点最多有两个孩子结点,那么第 i 层最多的结点数等于第 i - 1 层最多结点数的 2 倍。而第 1 层最多只有 1 个结点,所以我们可以知道第 i 层最多有 2i-1 个结点。
- 深度为 k 的二叉树最多有 2k - 1 个结点。由上一个性质,我们可以知道二叉树每层最多的结点个数,从第 1 层到第 k 层把最多结点数累加起来,我们就可以得到深度为 k 的二叉树最多有 2k - 1 个结点。
- 任意一棵二叉树上,其叶子结点个数 n0 比度为 2 的结点数 n2 多 1。度为 2 的结点指的是即有左孩子又有右孩子的结点。我们记树上结点总个数为 n,度为 1 的结点个数为 n1,则有 n = n0 + n1 + n2。另外我们可以发现一棵二叉树一共有 n - 1 条边,度为 2 的结点可以延伸出 2 条边,度为 1 的结点可以延伸出 1 条边,叶子结点没有边延伸出来,所以又有 n - 1 = n1 + 2 * n2。结合以上两个式子,我们可以得到 n0 = n2 + 1。
了解下两个特殊的二叉树:①第一个是满二叉树,如果一棵树深度为 k 而且有 2k - 1 个结点,那么我们称该二叉树为满二叉树,也就是说在此深度上,不能再添加结点了;②第二个是完全二叉树,如果一棵树深度为 k,从第 1 层到第 k - 1 层该树是满二叉树,第 k 层的结点都集中在左边,那么我们称该二叉树为完全二叉树。完全二叉树因其结构的特殊性具有很高的效率,它经常被用在算法的优化里。
5.二叉树的创建,存储,三种遍历
1 #include<iostream> 2 using namespace std; 3 class Node { 4 public: 5 int data; 6 Node *lchild, *rchild; 7 Node(int _data) { 8 data = _data; 9 lchild = NULL; 10 rchild = NULL; 11 } 12 ~Node() { 13 if (lchild != NULL) { 14 delete lchild; 15 } 16 if (rchild != NULL) { 17 delete rchild; 18 } 19 } 20 void preorder() { 21 cout << data << " "; 22 if (lchild != NULL) { 23 lchild->preorder(); 24 } 25 if (rchild != NULL) { 26 rchild->preorder(); 27 } 28 } 29 void inorder() { 30 if (lchild != NULL) { 31 lchild->inorder(); 32 } 33 cout << data << " "; 34 if (rchild != NULL) { 35 rchild->inorder(); 36 } 37 } 38 void postorder(){ 39 if(lchild!=NULL){ 40 lchild->postorder(); 41 } 42 if(rchild!=NULL){ 43 rchild->postorder(); 44 } 45 cout<<data<<" "; 46 } 47 }; 48 class BinaryTree { 49 private: 50 Node *root; 51 public: 52 BinaryTree() { 53 root = NULL; 54 } 55 ~BinaryTree() { 56 if (root != NULL) { 57 delete root; 58 } 59 } 60 void build_demo() { //存储二叉树 61 root = new Node(1); 62 root->lchild = new Node(2); 63 root->rchild = new Node(3); 64 root->lchild->lchild = new Node(4); 65 root->lchild->rchild = new Node(5); 66 root->rchild->rchild = new Node(6); 67 } 68 void preorder() { //先序 69 root->preorder(); 70 } 71 void inorder() { //中序 72 root->inorder(); 73 } 74 void postorder(){ //后序 75 root->postorder(); 76 } 77 }; 78 int main() { 79 BinaryTree binarytree; 80 binarytree.build_demo(); 81 binarytree.preorder(); 82 cout << endl; 83 binarytree.inorder(); 84 cout << endl; 85 binarytree.postorder(); 86 cout<<endl; 87 return 0; 88 }
6.已知先序和中序求后序
1 #include<iostream> 2 #include<string> 3 using namespace std; 4 class Node { 5 public: 6 int data; 7 Node *lchild, *rchild; 8 Node(int _data) { 9 data = _data; 10 lchild = NULL; 11 rchild = NULL; 12 } 13 ~Node() { 14 if (lchild != NULL) { 15 delete lchild; 16 } 17 if (rchild != NULL) { 18 delete rchild; 19 } 20 } 21 void postorder() { 22 if (lchild != NULL) { 23 lchild->postorder(); 24 } 25 if (rchild != NULL) { 26 rchild->postorder(); 27 } 28 cout << data << " "; 29 } 30 Node* build(const string &pre_str,const string &in_str,int len){ 31 Node *p=new Node(pre_str[0]-'0'); 32 int pos=in_str.find(pre_str[0]); 33 if(pos>0){ 34 p->lchild=build(pre_str.substr(1,pos),in_str.substr(0,pos),pos); 35 } 36 if(len-pos-1>0){ 37 p->rchild=build(pre_str.substr(pos+1),in_str.substr(pos+1),len-pos-1); 38 } 39 return p; 40 } 41 }; 42 class BinaryTree { 43 private: 44 Node *root; 45 public: 46 BinaryTree() { 47 root = NULL; 48 } 49 ~BinaryTree() { 50 if (root != NULL) { 51 delete root; 52 } 53 } 54 BinaryTree(const string &pre_str,const string &in_str,int len){ 55 root=root->build(pre_str,in_str,len); 56 } 57 void postorder() { 58 root->postorder(); 59 } 60 }; 61 int main() { 62 string pre_str = "136945827"; 63 string in_str = "963548127"; 64 BinaryTree binarytree(pre_str,in_str,in_str.length()); 65 binarytree.postorder(); 66 cout<<endl; 67 return 0; 68 }
7.哈夫曼编码是 1952 年由 David A. Huffman 提出的一种无损数据压缩的编码算法。哈夫曼编码先统计出每种字母在字符串里出现的频率,根据频率建立一棵路径带权的二叉树,也就是哈夫曼树,树上每个结点存储字母出现的频率,根结点到结点的路径即是字母的编码,频率高的字母使用较短的编码,频率低的字母使用较长的编码,使得编码后的字符串占用空间最小。
哈夫曼编码的步骤:
步骤一:从集合里取出两个根结点权值最小的树 a 和 b,构造出一棵新的二叉树 c,二叉树 c 的根结点的权值为 a 和 b 的根结点权值和,二叉树 c 的左右子树分别是 a 和 b。
步骤二:将二叉树 a 和 b 从集合里删除,把二叉树 c 加入集合里。
重复以上两个步骤,直到集合里只剩下一棵二叉树,最后剩下的就是哈夫曼树了。
举例:“good good study day day up”
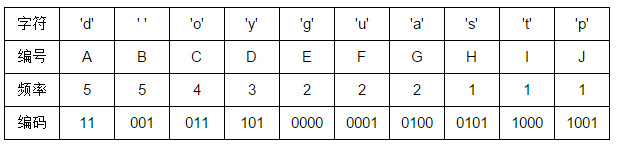
下面我们来算一下哈夫曼树的带权路径长度 WPL,也就是每个叶子到根的距离乘以叶子权值结果之和。
WPL = 5 * 2 + 5 * 3 + 4 * 3 + 3 * 3 + 2 * 4 + 2 * 4 + 2 * 4 + 1 * 4 + 1 * 4 + 1 * 4 = 82。
我们来算下如果直接存储字符串需要多少个比特,我们知道一个字符占一个字节,一个字节占 8 个比特,所以一共需要 8 * 26 = 208 个比特。我们再来看看哈夫曼编码需要多少个比特,我们可以发现 WPL 也就是编码后原来字符串所占的比特总长度 82。显然,哈夫曼编码把原数据压缩了好多,而且没有损失。
8.哈夫曼编码的性质
哈夫曼树上不会存在只有一个孩子结点的结点
在哈夫曼树上,相对来说,权值大的结点离根结点近,权值小的结点离根结点远
哈夫曼编码每次从集合里取出根结点权值最小的两棵二叉数构成新的二叉树


 浙公网安备 33010602011771号
浙公网安备 33010602011771号