GYM 101502I. Move Between Numbers

I. Move Between Numbers

time limit per test

memory limit per test

input

output

You are given n magical numbers a*1, *a*2, …, *a**n, such that the length of each of these numbers is 20 digits.

You can move from the i**th number to the j**th number, if the number of common digits between a**i and a**j is exactly 17 digits.

The number of common digits between two numbers x and y is computed is follow:

.

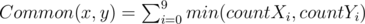Where countX**i is the frequency of the i**th digit in the number x, and countY**i is the frequency of the i**th digit in the number y.

You are given two integers s and e, your task is to find the minimum numbers of moves you need to do, in order to finish at number a**e*starting from number *a**s.

Input

The first line contains an integer T (1 ≤ T ≤ 250), where T is the number of test cases.

The first line of each test case contains three integers n, s, and e (1 ≤ n ≤ 250) (1 ≤ s, e ≤ n), where n is the number of magical numbers, s is the index of the number to start from it, and e is the index of the number to finish at it.

Then n lines follow, giving the magical numbers. All numbers consisting of digits, and with length of 20 digits. Leading zeros are allowed.

Output

For each test case, print a single line containing the minimum numbers of moves you need to do, in order to finish at number a**e starting from number a**s. If there is no answer, print -1.

Example

Copy

1
5 1 5
11111191111191111911
11181111111111818111
11811171817171181111
11111116161111611181
11751717818314111118

output

3

Note

In the first test case, you can move from *a*1 to *a*2, from *a*2 to *a*3, and from *a*3 to *a*5. So, the minimum number of moves is 3 moves.

题意

​ 给出n个20位的数，求第s到第e的最少步数。

​ 能走的条件是这样的： 如果两个数相同数字个数的和为17，那么就能互相到达。例如a1与a2公有17个1，那么可以互相到达，a2与a3公有14个1和3个8，它们的总和为17，则它们也可以互相到达。

解题思路

​ 建图，BFS(dijkstra也行)。

代码

#include<bits/stdc++.h>
using namespace std;
#define maxn 300
#define inf 0x3f3f3f3f

int number1[10],number2[10],flag[maxn];
string str[maxn];
vector<int> v[maxn];
int s,e;
struct node
{
    int x,step;
    node() {}
    node(int a,int b)
    {
        x=a;
        step=b;
    }
};
void bfs()
{
    memset(flag,0,sizeof(flag));
    queue<node> q;
    flag[s]=1;
    q.push(node(s,0));
    while(!q.empty())
    {
        node now=q.front();
        q.pop();
        flag[now.x]=1;
        if(now.x==e)
        {
            printf("%d\n",now.step);
            return;
        }
        for(int i=0; i<v[now.x].size(); i++)
        {
            node next=now;
            next.x=v[now.x][i];
            if(flag[next.x]) continue;
            next.step=now.step+1;
            q.push(next);
        }
    }
    printf("-1\n");
}
int main()
{
//    freopen("in.txt","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        cin>>n>>s>>e;
        for(int i=0;i<=n;i++)
            v[i].clear();
        for(int i=1; i<=n; i++)
            cin>>str[i];
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=n; j++)
            {
                memset(number1,0,sizeof(number1));
                memset(number2,0,sizeof(number2));
                for(int k=0; k<20; k++)
                {
                    number1[str[i][k]-'0']++;
                    number2[str[j][k]-'0']++;
                }
                int sum=0;
                for(int k=0; k<10; k++)
                    sum+=min(number1[k],number2[k]);
                if(sum==17) v[i].push_back(j);
            }
        }
        bfs();
    }
    return 0;
}