学习笔记 【关于 Tarjan 算法求 LCA （的思想）】
前言
原本觉得 \(\texttt {tarjan}\) 求 \(\texttt {LCA}\) 的做法有点废，因为它还要离线求，不适用于大多数要求 \(\texttt {LCA}\) 的题目，就没学，但是这几天发现有一道题目运用这个思想用的十分得妙，想再梳理一下。
做法
我们知道，树上任意两个点的 \(\texttt {LCA}\) 只有两种可能，一种是其中的一个点，一种同是属于另一个点的子树内。（好像是废话）
当我们用 \(\texttt {dfs}\) 遍历一颗树时，对于我们要求 \(\texttt {LCA}\) 的两个点，可进行讨论：
-
若一个点是另一个点的祖先，我们考虑做标记，从根节点到我们访问到的这个节点都标记一下，若访问到一个节点时，可以判断它的对应节点是否被标记，就简单的做完了。（记得要删除标记）
-
另一种情况有点烦，我们可以这样想，令三个点为 u ， v ，（ u 和 v 的 \(\texttt {LCA}\) ）k：首先要明确一点， u 和 v 在 k 的子树中，若我们先访问到 u ，当 u 回溯回去的时候，从 u 回溯到 k ，再从 k 向下走到 v 时，可以发现 u 到根节点所有点中最高（深度最浅）且没有回溯的点就是 k ，那我们就可以记录这个点，就可以轻松解决问题。
关于上面所述的点如何记录，可以使用（树上）并查集，若要回溯这个点，就将这个点并查集数组的值取为“父亲节点”，否则就为自己。
- 例子：要求 \(\texttt{LCA(3,2)}\) 和 \(\texttt{LCA(3,4)}\)
如图：
-
DFS 遍历到节点 3
-
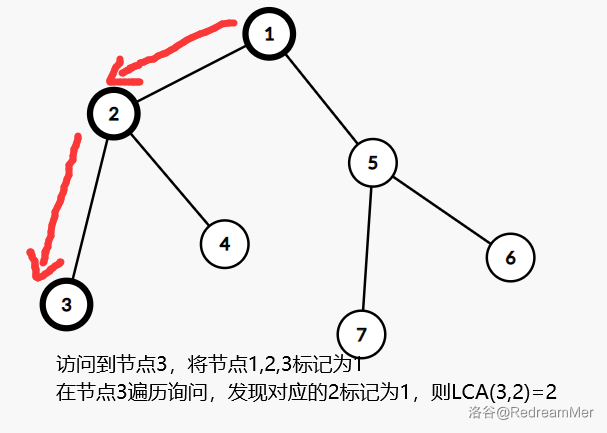
从节点 3 回溯，遍历到节点 4
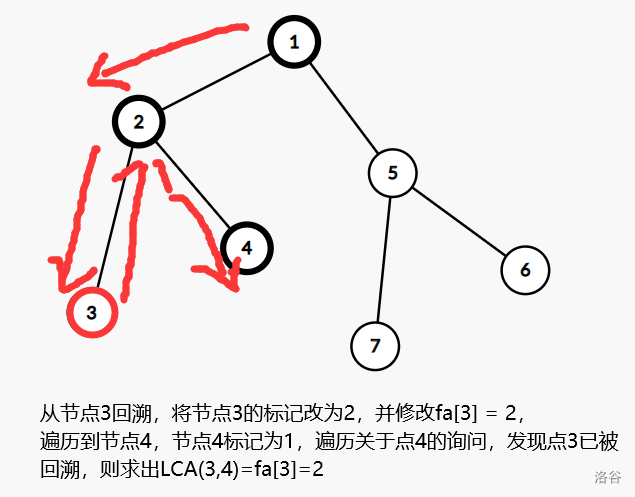
至此，解决问题，总复杂度为 \(\texttt{O(N + 2Q)}\)。
代码
#include <bits/stdc++.h>
using namespace std;
// #define ls now << 1
// #define rs now << 1 | 1
#define PB push_back
#define MP make_pair
// #define int long long
// #define us unsigned
// #define LL long long
const int N = 5e5;
// const int M = 255;
// #define re register
// const int mod = 1e9 + 7;
// const int inf = 1e18;
// const double inf_double = 1e4;
// const double eps = 1e-8;
// inline char nc()
// {
// static char buf[1000000], *p1 = buf, *p2 = buf;
// return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
// }
// #define getchar nc
//template <class Tp>
inline int read()
{
int s = 0;
register bool neg = 0;
register char c = getchar();
for (; c < '0' || c > '9'; c = getchar())
neg |= (c == '-');
for (; c >= '0' && c <= '9'; s = s * 10 + (c ^ 48), c = getchar())
;
s = (neg ? -s : s);
return s;
}
int a, b, c, vis[N + 10], f[N + 10], ans[N + 10];
vector<int> st[N + 10];
vector<pair<int, int>/**/> ask[N + 10];
inline int ff(int n) {return f[n] == n ? n : f[n] = ff(f[n]); }
inline void dfs(int n, int fa) {
vis[n] = 1;//已访问到
f[n] = n;
for(int i = 0; i < st[n].size(); i++) {
int v = st[n][i];
if(v == fa) continue;
dfs(v, n);
f[v] = n;
}
for(int i = 0; i < ask[n].size(); i++) {
int v = ask[n][i].second, p = ask[n][i].first;
if(!vis[v]) continue;
if(vis[v] == 1) ans[p] = v;
else ans[p] = ff(v);
}
vis[n] = 2;//已回溯
}
signed main()
{
a = read();
b = read();
c = read();
int x, y;
for(int i = 1; i < a; i++) {
x = read();
y = read();
st[x].PB(y);
st[y].PB(x);
}
for(int i = 1;i <= b; i++) {
x = read();
y = read();
ask[x].PB(MP(i, y));
ask[y].PB(MP(i, x));
}
dfs(c, 0);
for(int i = 1; i <= b; i++) printf("%d\n", ans[i]);
return 0;
}
例题
题目有点难找
- 洛谷P5838
(不要相信题解区一堆说ds的，线性可过)
双倍经验 SP11985 GOT
学会了Tarjan对于这道题目来说就是入门题目了，动态维护每种品种的牛奶的最低位置，询问时查找两个节点的最低值是否相同。
（具体见题解）
似乎比原求LCA更简单。/yiw
- 本校OJ原题
给定一个图，求所有最小生成树中每一条边是 必有、可有、没有 的。
看似有点模板，网上找一篇题解也没有。
思路：先求出一棵最小生成树先把树上所有边令为必有，建边，若有一条边与树上的边形成的环中有一条与它权值相等，那它就是可有的，另找到的那几条边也令为可有，这里加一点奇奇怪怪的乱搞优化可过。
上面那个结论：因为最小生成树保证它边权和已经是最小了，加了一条多余的边肯定要去掉一条边，取值和必定不变（不然就是棵假最小生成树），而这条边去掉要形成一棵树，那必定是在与树边形成的换上面的一条边。
Update：其实就是弱化的次小生成树板子，也可以带个log更好写，但是当时太菜没看出来QwQ。
