题解 【SP2916 GSS5 - Can you answer these queries V】

\(\large{\texttt{SP2916 GSS5}}\)

---

\(GSS\) 的线段树模板题目都非常得经典，可以都做一做。除了树剖题

前置知识：\(\texttt{SP1043 GSS1}\)的操作

---

\(\large{\texttt{Meaning}}\)

题目描述已经讲的十分清晰了，这里不做赘述，但是要强调一句话：

但是不保证端点所在的区间不重合

所以我们就要对此作出分类讨论（两种）。

---

\(\large{\texttt{Solution}}\)

首先，对于区间最大子段和，我们要熟练运用 \(GSS1\) 中的转移操作，即维护三个区间信息：左起最大子段和，右起最大子段和，区间最大子段和。

学会了这个，我们就要开始分类讨论这道题的情况。

1. 出现 \(y_1<x_2\)

即两个区间没有重合部分。

如图：

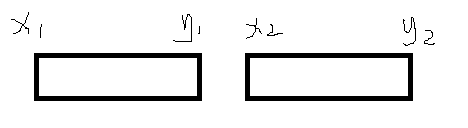
此时，我们只有一种选择方案：

区间 [\(x_1,y_1\)] 找到右起最大子段和，区间 [\(y_1+1,x_2-1\)] 的区间和，区间 [\(x_2,y_2\)] 找到左起最大子段和，三者相加就是这个询问的答案。

---

2. 出现 \(y_1\ge x_2\)

如图：

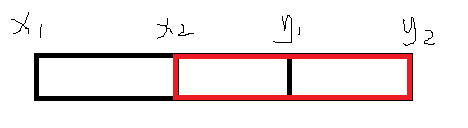
这个情况的特殊点在于，两个区间有重叠，那我们就不能考虑一种方案了。

分三种情况：

• 区间 \([x_2,y_1]\) 的区间最大子段和
• 区间 \([x_1,x_2]\) 的右起最大子段和 \(+\) 区间 \([x_2,y_2]\) 的左起最大子段和
• 区间 \([y_1,y_2]\) 的左起最大子段和 \(+\) 区间 \([x_1,y_1]\) 的右起最大子段和

这样这个询问的最优解就一定被计算到了，保证了答案的最优。

最后，就能保证所有的询问都是最优的答案。

---

\(\large{\texttt{Code}}\)

码量确实有点大，细节要注意下

#include <bits/stdc++.h>
using namespace std;

#define ls now<<1
#define rs now<<1|1
//#define int long long
const int N=10010;

int t,a,b,s1[N],l1,l2,r1,r2;
struct tree {
	int l,r,lmx,rmx,sum,mx;//l为区间做端点，r为区间右端点，lmx为左起最大子段和，rmx为右起最大子段和，sum为区间和，mx为区间最大子段和 
	tree operator+(const tree x)const {//用这种转移方式或许会更方便，转移方法详见GSS1 
		tree ans;
		ans.l=l;
		ans.r=x.r;
		ans.sum=sum+x.sum;
		ans.lmx=max(lmx,sum+x.lmx);
		ans.rmx=max(x.rmx,x.sum+rmx);
		ans.mx=max(rmx+x.lmx,max(mx,x.mx));
		return ans;
	}
} s[N<<2],ans;

inline void build(int now,int l,int r) {
	s[now].l=l;
	s[now].r=r;
	if(l==r) {
		s[now].sum=s[now].lmx=s[now].rmx=s[now].mx=s1[l];
		return;
	}
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
	s[now]=s[ls]+s[rs];
}
inline tree query(int now,int l,int r){//query的返回值最好是一颗线段树，方便处理 
	if(s[now].l>=l&&s[now].r<=r) return s[now];
	int mid=(s[now].l+s[now].r)>>1;
	if(l<=mid&&mid<r) return query(ls,l,r)+query(rs,l,r);
	if(l<=mid) return query(ls,l,r);
	else return query(rs,l,r);
}
inline int sum(int now,int l,int r){
	if(l>r) return 0;
	if(s[now].l>=l&&s[now].r<=r) return s[now].sum;
	int mid=(s[now].l+s[now].r)>>1,p=0;
	if(l<=mid) p+=sum(ls,l,r);
	if(mid<r) p+=sum(rs,l,r);
	return p;
}
signed main() {
//	freopen("in1.in","r",stdin);
	scanf("%d",&t);
	while(t--) {
		scanf("%d",&a);
		for(int i=1; i<=a; i++) scanf("%d",&s1[i]);
		build(1,1,a);
		scanf("%d",&b);
//		for(int i=1;i<=(a<<2);i++){
//			cout<<s[i].l<<' '<<s[i].r<<' '<<s[i].lmx<<' '<<s[i].rmx<<' '<<s[i].mx<<' '<<s[i].sum<<endl;
//		}
		for(int i=1; i<=b; i++) {
			scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
			if(r1<l2){//第一种情况 
				printf("%d\n",query(1,l1,r1).rmx+sum(1,r1+1,l2-1)+query(1,l2,r2).lmx);
			}
			else{//第二种情况 
				int f1=query(1,l2,r1).mx,f2=-0x7fffffff,f3=-0x7fffffff;//三种考虑方案，注意一开始变量的初始值设为-inf
				if(l2-1>=l1) f2=query(1,l1,l2-1).rmx+query(1,l2,r2).lmx;//注意两个区间的左端点是否重合，重合就不必考虑 
				if(r1+1<=r2) f3=query(1,r1+1,r2).lmx+query(1,l1,r1).rmx;//注意两个区间的右端点是否重合，重合就不必考虑
				printf("%d\n",max(f1,max(f2,f3)));
			}
		}
	}
	return 0;
}