12-15分治法的应用

分治法的应用

前提条件如图：

13.二分搜索

#include<iostream>
using namespace std;

const int N =  1e6;
int n,m;
int q[N];
//对于二分分界来说左加右减
//对于取中值来说，男左女右，男是1，不用+，女需要+1
int main()
{
  cout<<"请输入数组个数以及查寻的数的个数"<<endl;
  cin>>n>>m;
  cout<<"请输入数组"<<endl;
  for(int i = 0 ;i<n;i++)cin>>q[i];
  while(m--)
  {
      int target;
      cin>>target;
      int left = 0;
      int right = n-1;
      //左边界
      while(left<right)
      {
          int mid = (left+right)/2;
          if(q[mid]>=target) right=mid;
          else left = mid+1;
      }
      //是否找到
      if(q[left]!=target)cout<<"-1 -1"<<endl;
      //右边界
      else
      {
      cout<<left<<" ";
      right = n-1;
      while(left<right)
      {
          int mid = (left+right+1)/2;
          if(q[mid]<=target)left = mid;
          else right=mid-1;
      }
      cout<<left<<endl;
      }
  }
  return 0;
}

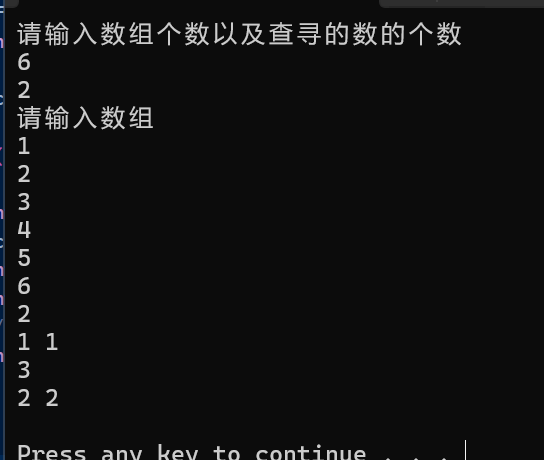
运行结果是这样的：

运用递归的二分的时间复杂度：

14.矩阵乘法和归并排序

归并排序：

代码如下：

#include<iostream>
using namespace std;

const int N = 1e6+10;

int n;
int q[N],tmp[N];

void merge_sort(int q[],int l,int r)
{
    if(l>=r)return ;
    int mid = (r+l)/2;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    int k = 0,i = l,j = mid +1;
    while(i<=mid&&j<=r)
    {
        if (q[i]<q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }  
    while(i<=mid)tmp[k++] = q[i++];
    while(j<=r)tmp[k++] = q[j++];

    for(i = l,j=0;i<=r;i++,j++)q[i]=tmp[j];

}

int main()
{
    scanf("%d",&n);
    for(int i = 0;i<n;i++)scanf("%d",&q[i]);

    merge_sort(q,0,n-1);

    for(int i = 0;i<n;i++)printf("%d\t",q[i]);
    return 0;
}

15快速排序算法

#include <iostream>
using namespace std;
const int N = 100010;
int q[N];

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
    quick_sort(q, 0, n - 1);
    for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
    return 0;
}