1-11一些时间复杂度的证明
时间复杂度的证明
1.大O原理
如图所示,大O原理,只取最高的复杂度

2.加法原理
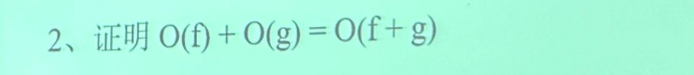
想要证明这个
首先,根据大O定义:
F(N) <= C1f(N)
G(N) <= C2g(N)
再把两者合并起来:
F(N)+G(N) <= C1f(N)+C2g(N)
设C3 = max(C1,C2)
则F(N)+G(N) <= C3(f(N)+g(N))
所以O(f)+O(g) <= O(f+g)
具体证明如图:

3.最大时间复杂度
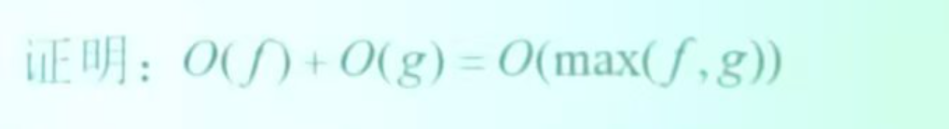
首先,根据大O定义:
F(N) <= C1f(N)其中N>=N1
G(N) <= C2g(N)其中N>=N2
构造N3=max(N1,N2)
那么对于N>=N3
F(N) <= C1f(N)
G(N) <= C2g(N)
再构造
h(N)=max(f(N),g(N))
C3=max(C1,C2)
那么可以得到<=
F(N)<=C1f(N)<=C1h(N)<=C3h(N)
G(N)<=C2g(N)<=C2h(N)<=C3h(N)
最后将两者合并一下可以得到
F(N)+G(N) <= 2C3h(N)
O(f)+O(g) = O(max(f,g))


4.乘法原理
如图所示,非常清晰
和上一个的区别是
构造
C3 = C1C2
h(N) = f(N)g(N)
N3仍然=max{N1,N2}

5如题

ai的思路更为清晰

6时间复杂度的不同阶数
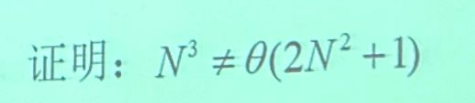
证明过程如图:


7和8
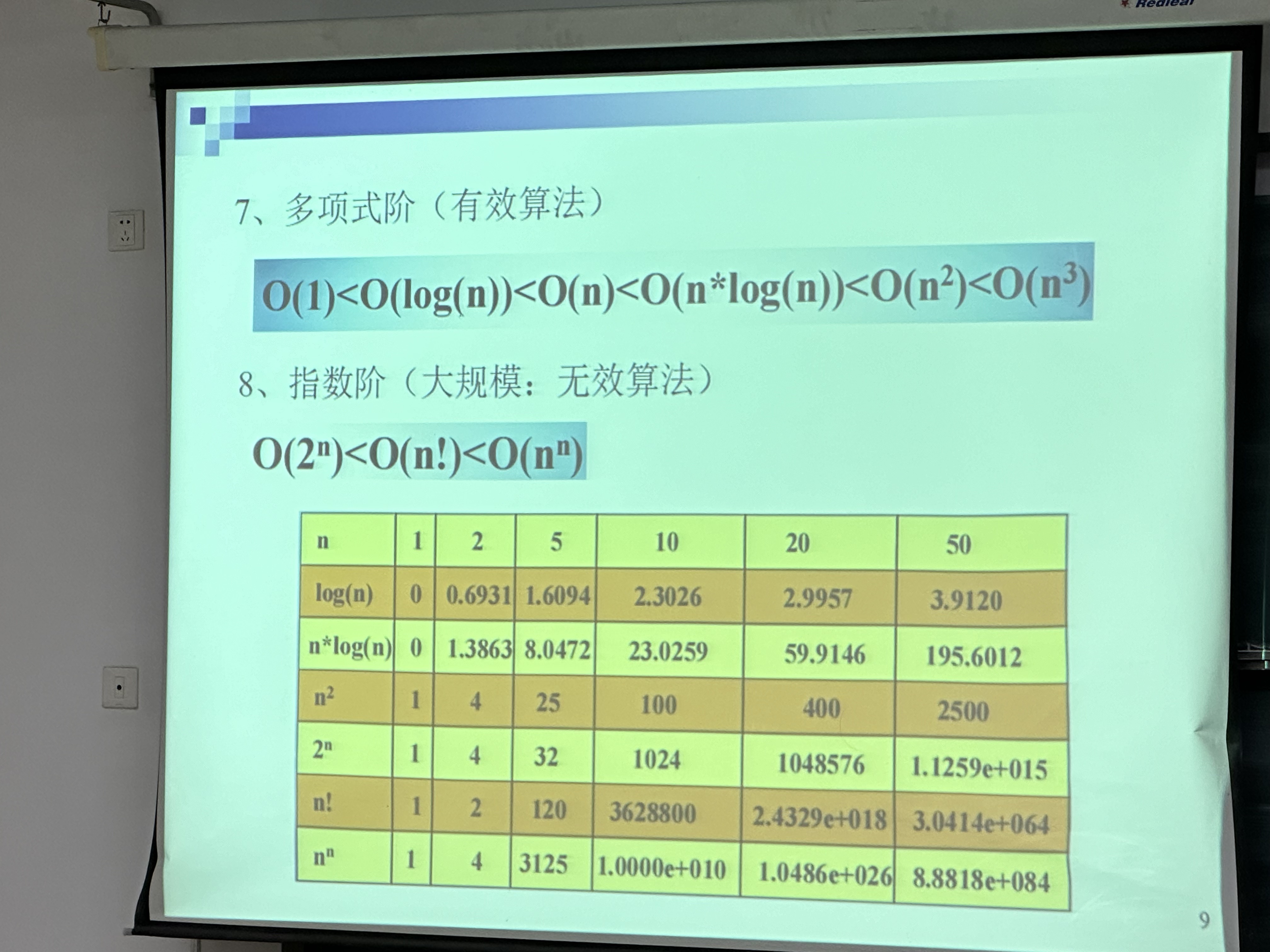
9几种基础算法的时间复杂度



10证明如下的等式

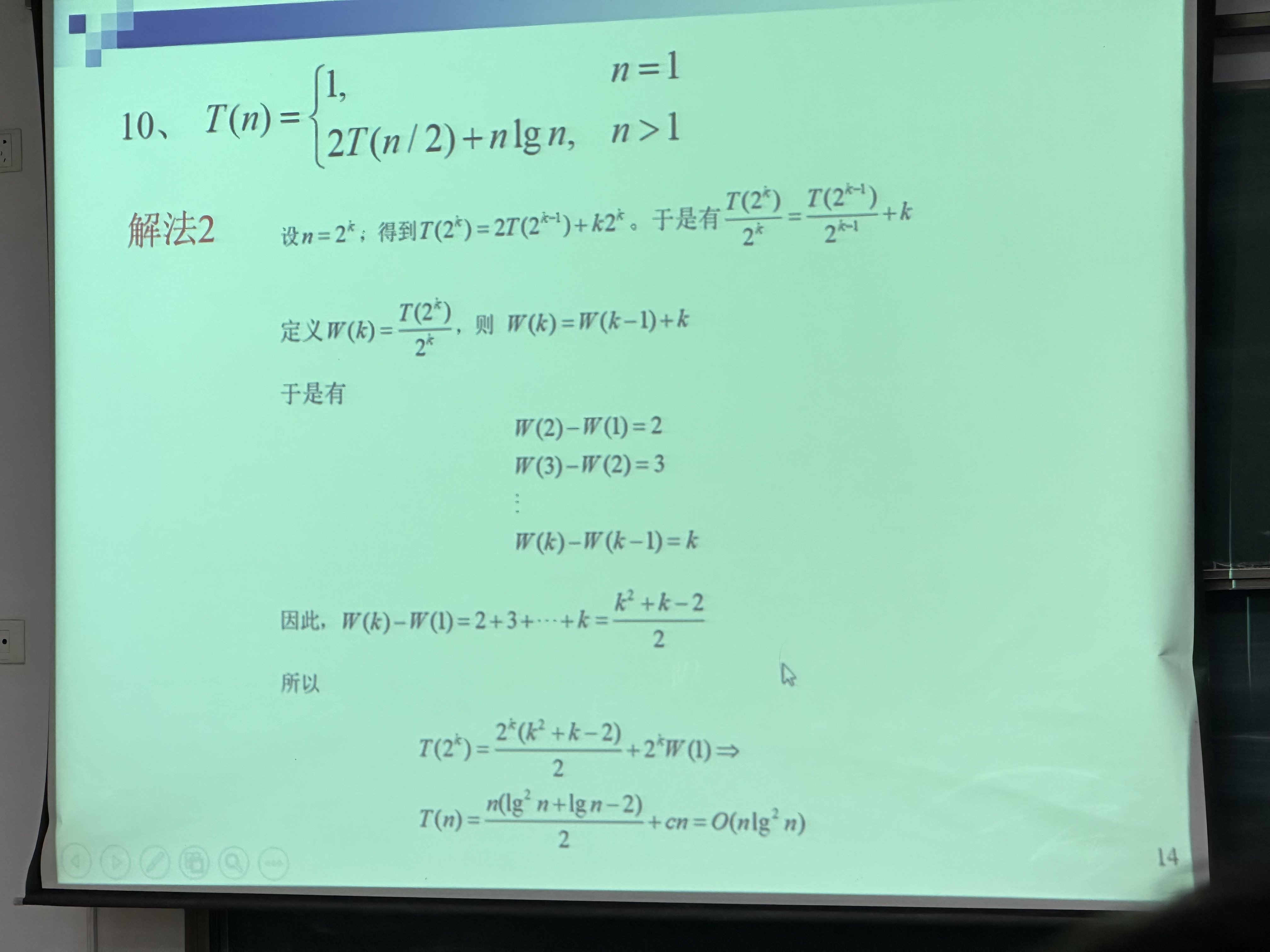
11证明如下的等式




 浙公网安备 33010602011771号
浙公网安备 33010602011771号