贝叶斯决策

基础概念

先验概率

根据先前的经验，也就是对某些类别预先知道的知识，对样本进行预测的概率。

似然概率

先验概率描述的根据现有知识，预测样本属于某一类的概率，是一个统计信息量。比如5个球中，有3个黑球，则黑球的概率是3/5。

似然概率描述的是已知样本属于某一类，预测样本特征x分布的概率。

后验概率

后验概率是对先验概率的修正，描述的是已知样本特征x，预测其属于某一类的概率。

极大似然估计

在传统问题中，通常概率分布模型的参数θ是已知的，而样本x是未知的。但是在机器学习中相反，通常是样本x已知，需要估计模型的参数θ，这就是似然估计。

极大似然估计就是在给定样本x情况下，根据其分布，计算概率最大的θ。

过程

对于已知样本x，x的概率为，极大似然估计是将θ看成变量，求使得p(x|θ)最大的参数θ.

x关于θ的似然函数 L(θ)=p(x|θ)

假设现在有样本X={x₁,b₂,...,x_n}，需要估计模型参数θ={θ₁,θ₁,...,θn}，则在给参数θ下，X的条件概率为：

现在求函数L(θ)的极值，为了便于求导，对L(θ)取对数，将L(θ)从连乘变成相加：

之后对参数求导求极值即可：

对于不同分布，计算方式也不同。

正态分布，但是参数均值μ未知的情况

对于均值μ求导并求极值：

高斯分布：均值μ和方差Σ均未知

根据上述得到：

 

对ln p(x_i | μ，Σ)求梯度算子：

 

得到极值：

 

贝叶斯公式

贝叶斯公式建立了先验概率和后验概率之间的联系。

p(x)为全概率公式，描述的是根据所有类别预测样本x的概率。

通常在同一概率分布下进行分类，p(x)是归一化因子，是一个常数，可以忽略，得到贝叶斯公式常用的形式。

 

贝叶斯估计

贝叶斯估计就是利用贝叶斯公式，根据已知样本集合求出样本的联合分布，再求参数的后验分布。

贝叶斯估计基本步骤

计算参数θ的先验概率分布p(θ)

根据样本集合D={x1,x2,...,xn}计算出联合分布p(D|θ)。

利用贝叶斯估计参数后验概率分布。

计算样本的后验概率密度。

高斯情况——方差σ已知，均值μ未知

假设

假设样本x在给定参数μ的情况下，呈现高斯分布：

并且均值也服从高斯分布：

 

估计均值的后验概率

假设样本均值μ的先验分布也是正态分布，先验分布的均值为μ₀，方差为σ₀²：

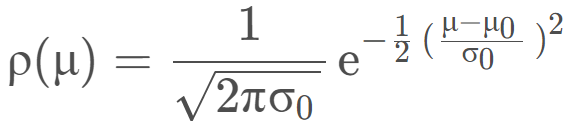
且样本在参数θ下的联合概率分布如下：

根据n个样本分布D，来估计均值μ的后验分布

令

代入可以得到：

      

其中α''是于μ无关的项。上述式子是关于μ的二次函数

p(μ|D)实质上还是一个正态分布。

正态分布对任意大小的样本集都成立，p(μ|D)随着样本个数n增加，始终保持正态分布。

因此对于所有样本N有：

对比两个式子得到：

令样本均值：

解得：

其中μ₀和σ₀都是先验分布的均值和方差。\hat{ μ }为样本的均值，且样本方差σ已知。则可以估计整体样本的均值和方差。

σ_N²关于n单调递减，也就是每增加一个样本，对μ的估计的不确定程度就更少。

估计似然概率

至此获得了样本的均值，便可以获取样本的分布。

其中：

上述式子中，方差σ_N和均值μ_N已经求得，且方差σ是已知项。

p(x|D)是一个正态分布，均值为μN，方差为σ²+σ_N²

因此计算后验概率密度函数p(x|D)时，只需要使用μ_N替换μ，σ²+σ_N²替换σ²即可计算。